9.2. Метод решения.

С истему уравнений (30) удобно представить в матричной форме [27]:

_(9.26)

где

_(9.27)

Поскольку направление намагниченности во втором слое меняется в пространстве, удобно перейти к локальной системе координат с помощью матрицы поворота:

, (9.28)

где .

Умножим уравнение (9.26) слева на матрицу

(9.29)

Получим новое матричное уравнение вида:

_(9.30)

где

_(9.31)

После этого преобразования мы получим систему дифференциальных уравнений с постоянными коэффициентами для нахождения .

В Приложении показан расчет матриц в общем случае, когда намагниченность слоя изменяется по закону :

_(9.31)

Задачу о бислое ферромагнетик/спиновая спираль можно рассматривать как частный случай при и .

Основное матричное уравнение для слоя :

_(9.32)

где - Лапласиан. Матричное уравнение для слоя имеет более простой вид, так как не содержит члены, пропорциональные Q.

Решение в обоих слоях ищется в виде:

(9.33)

где принимает дискретные значения.

Подстановка решения в таком виде в систему (30) позволяет определить как функции . Для нахождения окончательного вида решения, необходимо записать условия непрерывности для и трех компонент вектора , а также для всех компонент спинового и электрического тока. После преобразования Фурье, получим систему линейных рекуррентных уравнений для определения неизвестных констант , которую можно схематично записать в виде:

_(9.34)

где ψ, φ, χ – известные функции . Эта система была решена численно с помощью стандартного математического пакета Mathematica 6.0 [28, 29].

9.3. Описание полученных результатов.

9.3.1. Система с полубесконечными слоями.

В этом разделе представлены результаты для спиновой аккумуляции, спинового торка, спинового и электрического токов в системе, состоящей из двух полубесконечных слоев, то есть в бесконечном бислое . В качестве численных значений параметров взяты , , параметр спиновой поляризации . Величина плотности электрический тока, протекающего в положительном направлении оси х перпендикулярно плоскости слоев, равна при сопротивлении ферромагнитного слоя (случай железа).

1. Спиновая аккумуляция.

Прежде всего, нас интересуют две компоненты вектора спиновой аккумуляции, перпендикулярные направлению намагниченности в слое . Первая из них – это , а другая может быть записана в форме (перпендикуляр к плоскости (yz)). Графики зависимостей этих компонент от координат y и x в безразмерных единицах приведены на рисунках 12а,б и 13а,б соответственно.

Изображенные на графиках функции являются периодическими функциями координаты y вблизи границы c периодом . В данном случае Q=1 , и графики зависимостей двух компонент вектора спиновой аккумуляции от y построены на интервале , что соответствует одному полупериоду спиновой спирали (ориентация вектора намагниченности в меняется от параллельной к антипараллельной относительно положительного направления оси z).

Рис. 12а. Зависимость от y при x = 0.

Рис. 12б. Зависимость от х при y = π/2.

Рис. 13а. Зависимость от y при х = 0.

Рис. 13б. Зависимость от х при y = π/2.

Поскольку система имеет бесконечные размеры, в решении (39) оставлены лишь затухающие экспоненты. Таким образом, функции и убывают с ростом х и становятся равными нулю вдали от границы слоев.

б) Спиновый торк.

Две компоненты вектора спиновой аккумуляции, описанные выше, связаны с двумя соответствующими компонентами спинового торка, поскольку , где - магнетон Бора. Первая компонента лежит в плоскости (yz), это так называемый адиабатический торк. Вторая компонента перпендикулярна этой плоскости и представляет собой неадиабатический вклад.

Графики зависимостей и показаны на рисунке 14а,б. Соответствующие графики для компоненты представлены на рисунке 15 а,б. Так же как и компоненты вектора спиновой аккумуляции, и являются периодическими функциями координаты y вблизи границы c периодом , а и убывают с ростом x. Наибольший интерес представляет неадиабатический торк , действующий на намагниченность слоя в направлении, перпендикулярном плоскости ее вращения. Также следует отметить, что в данном случае больше по величине, чем адиабатический торк

Рис. 14а. Зависимость от y при x = 0.

Рис. 14б. Зависимость от x при y = π/2.

Рис. 15а. Зависимость от y при х = 0.

Рис. 15б. Зависимость от х при y = π/2.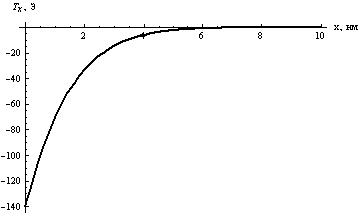

в) Электрический ток

Компонента вектора плотности электрического тока, протекающего вдоль оси х, является осциллирующей функцией от y при x=0 и вблизи границы слоев (см. рис. 16), но осцилляции уменьшаются с ростом x, и график зависимости выходит на константу вдали от границы .

_{Это значение несколько меньше плотности электрического тока, проходящего через ферромагнитный слой, следовательно, можно сделать вывод о том, что граница между слоями дает вклад в сопротивление.}

Зависимость от x при трех различных значениях y (0, и ) представлены на рисунках 17а, 17б, 17в соответственно. На всех трех рисунках штриховой линией показано значение

Рис. 16. Зависимость от y при x = 0.

Рис. 17а. Зависимость от x при y = 0.

Штриховой линией показано

Рис. 17б. Зависимость от x при y= π/2.

Штриховой линией показано

Рис. 17в. Зависимость от x при y=π.

Штриховой линией показано

Другая компонента вектора плотности электрического тока также является осциллирующей функцией от координаты y вблизи границы слоев. Эта функция меняет знак, а амплитуда колебаний составляет по порядку величины. Наличие электрического тока в направлении, перпендикулярном направлению электрического поля, можно объяснить в терминах эффекта Холла.

На рисунках 18а, 18б показаны зависимости от x и y соответственно.

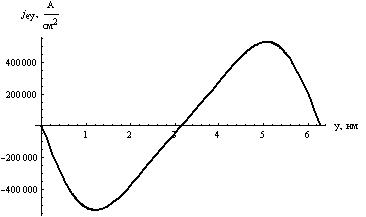
Рис. 18а. Зависимость от y при x = 0.

Рис. 18б. Зависимость от x при y = π/2.

г) Спиновый ток

На рисунках 19 – 24 показаны графики для компонент спинового тока, определенного по формулам (22). Здесь приняты следующие обозначения: , .

Компонента является осциллирующей функцией y при x=0 и вблизи границы (см. рис. 19а) и равна нулю вдали от границы (см. рис. 19б).

Рис. 19а. Зависимость от y при x = 0.

Рис. 19б. Зависимость от x при y = π/2.

Компонента также является осциллирующей функцией y при x=0 и вблизи границы (см. рис. 20а), но при y=π/2 график зависимости выходит на ненулевую константу (см. рис. 20б).

Существование ненулевого магнитного тока вдали от границы, можно объяснить непосредственно с помощью выражения для тока:

_(9.36)

При y = π/2 и Q=1 угол θ = π/2, то есть намагниченность в слое направлена вдоль оси y. Тогда:

_(9.37)

Вклад обеспечивает существование ненулевого магнитного тока вдоль оси y вдали от границы слоев.

Рис. 20а. Зависимость от y при x = 0.

Рис. 20б. Зависимость от x при y = π/2.

В случае ненулевой магнитный ток возможен при y=0 и y=π (см. рис. 21б, г), поскольку при этих значениях y и Q=1 угол θ равен соответственно 0 или π, то есть намагниченность в слое направлена вдоль оси z. Тогда:

_(9.38)

Вклад обеспечивает существование ненулевого магнитного тока вдоль оси z вдали от границы слоев.

При x=0 и вблизи границы слоев компонента является осциллирующей функцией y (см. рис. 21а ).

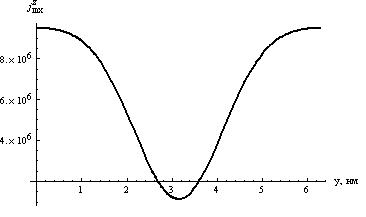
Рис. 21а. Зависимость от y при x = 0.

Рис. 21б. Зависимость от x при y = 0.

При y = π/2 и больших x компонента становится равной нулю (см рис. 21в).

Рис. 21в. Зависимость от x при y = π/2.

Рис. 21 г. Зависимость от x при y = π.

Что касается вектора , то все его компоненты являются осциллирующими функциями координаты y при x=0 и вблизи границы (см. рис. 22а, 23а, 24а ), и равны нулю вдали от границы, что подтверждается соответствующими графиками (см. рис. 22б - г, 23б – г, 24б).

Рис. 22a. Зависимость от y при x = 0.

Рис. 22б. Зависимость от x при y = 0.

Рис. 22в. Зависимость от x при y = π/2.

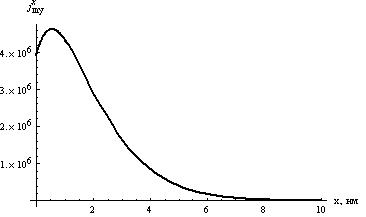
Рис. 22г. Зависимость от x при y = π.

Рис. 23а. Зависимость от y при x = 0.

Рис. 23б. Зависимость от x при y = 0.

Рис. 23в. Зависимость от x при y = π/2.

Рис. 23г. Зависимость от x при y = π.

Рис. 24 а. Зависимость от y при y = 0.

Рис. 24б. Зависимость от x при y = π/2.