1.2. Дифференцирующие цепи

Дифференцирующей цепью (ДЦ) называется четырехполюсник, выходной сигнал которого пропорционален в каждый момент времени производной от входного сигнала. Простейшие ДЦ показаны на рис. 6 [3].

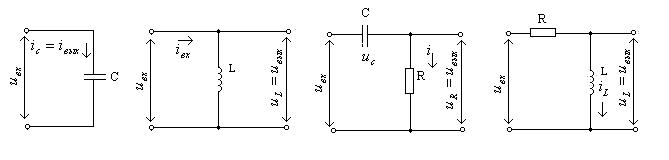
Рис. 6. Дифференцирующие цепи: а – емкостная; б – индуктивная; в – емкостно-резистивная; г – резистивно-индуктивная

В емкостной ДЦ (рис. 6, а) ток через конденсатор есть производная от входного напряжения:

. (23)

В индуктивной ДЦ (рис. 6, б) выходное напряжение есть производная от входного тока:

(24)

Однако наибольшее применение в практике находит емкостно-резистив­ная и резистивно-индуктивная ДЦ (рис. 6, в, г), в которых входными и выходными величинами является напряжение. Из них резистивно-индуктивная R-L ДЦ применяется реже, так как для неё необходима катушка индуктивности или дроссель с достаточно большой индуктивностью, которые получаются конструктивно громоздкими с большой межвитковой емкостью, которая, в свою очередь, вносит существенную ошибку в результат дифференцирования [3].

Операцию дифференцирования, выполняемую емкостно-резистивной C-R ДЦ, можно в общем виде записать [7]:

(25)

где k – коэффициент пропорциональности.

1.2.1. Принцип работы схемы

Конденсатор (без утечки) является идеальным элементом для преобразования приложенного к нему напряжения u₁ (рис. 7) в ток i, изменяющийся пропорционально производной du₁/dt.

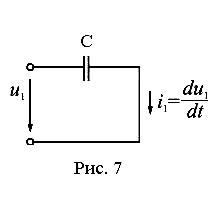
Рис. 7

Для получения выходного напряжения, изменяющегося по закону

, (26)

достаточно преоб­разовать протекающий в цепи ток i в напряжение.

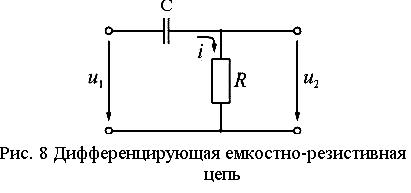
Рис. 8. Дифференцирующая емкостно-резистивная цепь

Это мо­жет быть достигнуто включением в цепь резистора R (рис. 8) настолько малого сопротивления, что закон изменения тока останется почти неизменным ( ), а создаваемое им падение напряжения будет изменяться по закону, близкому к (26).

При этих условиях неизменности тока напряжение на выходе пренебрежимо мало по сравнению с входным и будет определяться полностью падением напряжения на резисторе R; т.е. при получаем результат дифференцирования входного напряжения:

. (27)

Несложный анализ показывает, что условие дифференцирования выполняется тем лучше, чем меньше постоянная времени , хотя при этом меньше полезное напряжение на выходе схемы [3, 5].

Действительно, согласно 2-му закону Кирхгофа для этой цепи дифференциальное уравнение имеет вид

. (28)

Если

(29)

то приближенно

(30)

т.е. схема практически выполняет дифференцирование [5]. Однако если условие (29) не выполнено или соотношение (29) противоположное, т.е.

(31)

то из (28) имеем

. (32)

Таким образом, при больших схема практически не дифференцирует, приближаясь к условию (31) крайне «медленных сигналов»; напротив, при малых схема соответствует условию (29) «быстрых сигналов», т.е. условию качественного дифференцирования [5].

Из вышеуказанного следует, что при выполнении условия (29), при ко­тором

, (33)

достигается достаточная точность дифференцирования, поэтому для качественного дифференцирования импульсных сигналов длительность входного импульса должна быть значительно больше постоянной времени переходного процесса :

. (34)

О качестве дифференцирования схемой прямоугольного импульса длительностью t можно судить из графиков для различных соотношений между длительностью импульса и постоянной времени цепи (рис. 9).

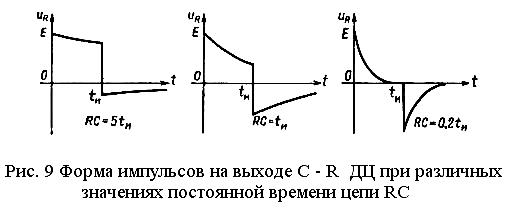
Рис. 9. Форма импульсов на выходе C-R ДЦ при различных значениях постоянной времени цепи RC

Как показано на рис. 9, с увеличением реакция цепи в виде выходного напряжения на резисторе (тока через конденсатор) все более приближается по форме к входному импульсу, и в дальнейшем цепь становится «переходной», т.е. прекращает дифференцирование и пропускает импульс практически без искажений [4].

Для синусоидальных входных напряжений условием дифференцирования согласно (33) должно быть соотношение:

(35)

где – циклическая частота, а – текущая частота синусоидального напряжения, Гц.

Коэффициент передачи дифференцирующей C-R цепи определяется формулой [5]

(36)

и при условии (35) имеет вид

, (37)

где – коэффициент передачи идеального четырехполюсника.

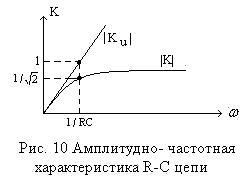
Рис. 10. Амплитудно-частотная характеристика R-C цепи

Реакцию цепи на синусоидальное воздействие наглядно отображает АЧХ (рис. 10), из которого видно, что при высоких частотах схема не дифференци-рует, удовлетворительное дифференцирование начинается ниже частоты

(38)

и в дальнейшем с ее понижением качество дифференцирования улучшается, т.е. для качественного дифференцирования входная функция не должна содержать высоких частот и их высших гармоник [5].

Из рассмотрения АЧХ (рис. 10) также можно сделать вывод, что данная C-R цепь может выполнять функцию фильтра верхних частот (ФВЧ) с нижней граничной частотой полосы пропускания :

(39)

т.е. от значения частоты и выше начинается полоса пропускания ФВЧ, а ниже этого значения полоса непропускания, в пределах которой коэффициент передачи уменьшается в вплоть до нуля.

Приближенная длительность полученных двух выходных импульсов при подаче на вход прямоугольного импульса с длительностью определяется соотношением [3]:

, (40)

т.е. интегрирование всегда сопровождается «укорочением» длительности импульса, поэтому в инженерной практике дифференцирующую цепь называют «укорачивающей».

Значение величины 3RC, как и для интегрирующей цепи, обусловлено процессом воздействия на конденсатор электромагнитной энергии входного импульса, при котором имеют место переходные процессы при заряде конденсатора в момент включения импульса и его разряде в момент отключения. Как упомянуто выше, практическое время заряда и разряда составляет в результате чего на выходе формируются два укороченных импульса с различной полярностью, конечной длительностью и конечной амплитудой [3]. В инженерной практике для целей укорочения импульса считают достаточным соотношение

(41)

Временные диаграммы, поясняющие процесс дифференцирования в C-R ДЦ, отображены на рис. 11.

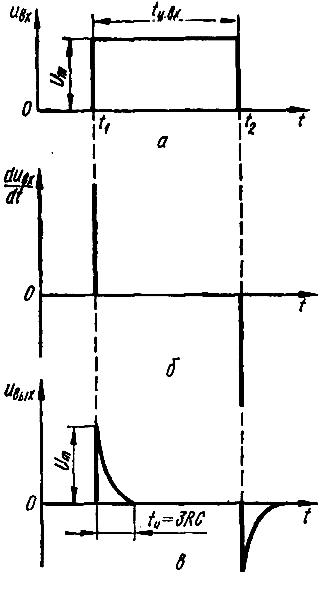
Рис. 11. Временные диаграммы напряжений дифференцирующей цепи: а – на входе; б – производной от входного напряжения; в – на выходе

При указанных выше условиях дифференцирования аналогичными свойствами обладает R-L дифференцирующая цепь (рис. 6, г).

Действительно, при ток и напряжение определяются соотношениями:

(42)

(43)

т.е. R-L ДЦ (рис. 6, г) также выполняет функцию дифференцирования. В формуле (43) – постоянная переходного процесса в ДЦ R-L, показывающая время, в течение которого выходное напряжение убывает в «е» раз. За время ток в цепи (напряжение на резисторе) достигает 0,99 от установившегося значения, т.е. переходный процесс можно считать законченным. Применительно к рис. 11 для этой цепи координата соответствует обозначению .

Дифференцирующие цепи применяются в аналоговых вычислительных устройствах для выполнения математической операции дифференцирования, в импульсной технике – для формирования прямоугольных импульсов напряжения (тока) пилообразной формы и остроконечных импульсов запуска различных устройств цифровой техники, а также в радиотехнических устройствах – в качестве звеньев фильтров верхних частот [3, 5].

Следует отметить, что с помощью рассмотренных простейших формирующих интегрирующих и дифференцирующих цепей принципиально невозможно осуществить точные операции интегрирования и дифференцирования, а лишь, как было отмечено выше, приближенные.

Современные дифференцирующие и интегрирующие устройства строятся на основе операционных усилителей, с помощью которых реализуются реальные схемы с хорошим дифференцированием в диапазоне нижних частот и реальные схемы с хорошим интегрированием в диапазоне верхних частот [8].