Свойства определенного интеграла
Дифференциальное
и интегральное исчисление / Свойства
определенного интеграла
|
|
|
|
|
Задание
N 6.
|
Среднее
значение функции
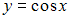 на
отрезке
на
отрезке
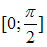 равно…
равно…
|
|
Варианты
ответа:
|
|
|
1
Ответ
неверный!
Среднее
значение функции
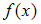 на
отрезке
на
отрезке
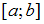 вычисляется
по формуле
вычисляется
по формуле
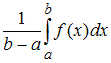 .
.
|
|
|
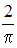
|
|
|
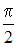
Ответ
неверный!
Среднее
значение функции
на
отрезке
вычисляется
по формуле
.
|
|
|
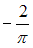
Ответ
неверный!
Среднее
значение функции
на
отрезке
вычисляется
по формуле
.
|
|
|
|
Решение:
Среднее
значение функции
на
отрезке
вычисляется
по формуле
.
Тогда:
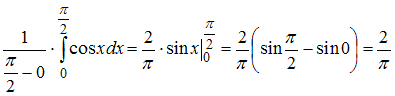
Дифференциальное
и интегральное исчисление / Свойства
определенного интеграла
|
|
|
|
|
Задание
N 8.
|
Среднее
значение функции
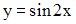 на
отрезке
на
отрезке
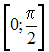 равно
…
равно
…
|
|
Варианты
ответа:
|
|
|
|
|
|
1
|
|
|
|
|
|
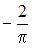
|
|
|
Решение:
Среднее
значение функции
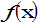 на
отрезке
на
отрезке
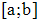 вычисляется
по формуле:
вычисляется
по формуле:
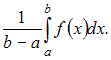 Тогда:
Тогда:
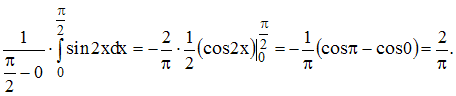
Дифференциальное
и интегральное исчисление / Свойства
определенного интеграла
|
|
|
|
|
Задание
N 6.
|
Если
функция
непрерывна
на отрезке
 и
и
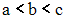 ,
то интеграл
,
то интеграл
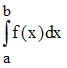 можно
представить в виде …
можно
представить в виде …
|
|
|
Варианты
ответа:
|
|
|
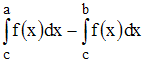
Ответ
неверный!
В
рассматриваемом случае точка
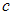 находится
вне отрезка
находится
вне отрезка
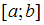 .
Тогда из свойств определенного
интеграла следует, что
.
Тогда из свойств определенного
интеграла следует, что
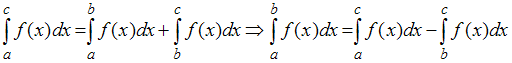 .
.
|
|
|
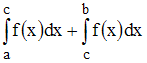
|
|
|
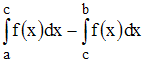
Ответ
неверный!
В
рассматриваемом случае точка
находится
вне отрезка
.
Тогда из свойств определенного
интеграла следует, что
.
|
|
|
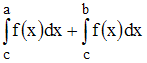
Ответ
неверный!
В
рассматриваемом случае точка
находится
вне отрезка
.
Тогда из свойств определенного
интеграла следует, что
.
|
|
|
|
Решение:
В
рассматриваемом случае точка
находится
вне отрезка
.
Тогда
из свойств определённого интеграла
следует, что
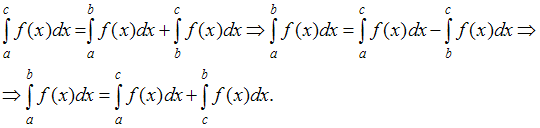 Замечание.
Свойство аддитивности интеграла
справедливо для точки
,
расположенной как внутри отрезка
,
так и вне этого отрезка, при условии
интегрируемости функции на соответствующих
отрезках.
Замечание.
Свойство аддитивности интеграла
справедливо для точки
,
расположенной как внутри отрезка
,
так и вне этого отрезка, при условии
интегрируемости функции на соответствующих
отрезках.
Дифференциальное
и интегральное исчисление / Свойства
определенного интеграла
|
|
|
|
|
Задание
N 8.
|
Если
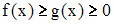 на
,
то значение определённого интеграла
на
,
то значение определённого интеграла
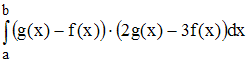 …
…
|
|
Варианты
ответа:
|
|
|
неположительно
Ответ
неверный!
Из
условия задачи следует, что
подынтегральная функция
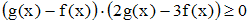 на
отрезке
.
на
отрезке
.
|
|
|
отрицательно
Ответ
неверный!
Из
условия задачи следует, что
подынтегральная функция
на
отрезке
.
|
|
|
положительно
Ответ
неверный!
Из
условия задачи следует, что
подынтегральная функция
на
отрезке
.
|
|
|
неотрицательно
|
|
|
Решение:
Из
условия задачи следует, что подынтегральная
функция
на
отрезке
.
Следовательно, значение интеграла
 неотрицательно.
неотрицательно.
Дифференциальное
и интегральное исчисление / Свойства
определенного интеграла
|
|
|
|
|
Задание
N 6.
|
Если
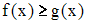 на
на
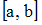 ,
то значение определённого интеграла
,
то значение определённого интеграла
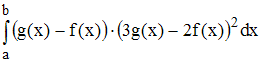 …
…
|
|
Варианты
ответа:
|
|
|
неотрицательное
Ответ
неверный!
Из
условия задачи следует, что
подынтегральная функция на отрезке
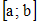 удовлетворяет
неравенству
удовлетворяет
неравенству
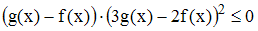 .
.
|
|
|
неположительное
|
|
|
положительное
Ответ
неверный!
Из
условия задачи следует, что
подынтегральная функция на отрезке
удовлетворяет
неравенству
.
|
|
|
отрицательное
Ответ
неверный!
Из
условия задачи следует, что
подынтегральная функция на отрезке
удовлетворяет
неравенству
.
|
|
|
Решение:
Из
условия задачи следует, что подынтегральная
функция удовлетворяет неравенству
,
т.е. является не положительной на отрезке
.
Следовательно, значение интеграла
удовлетворяет неравенству
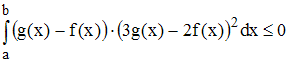 и
тоже является не положительным.
и
тоже является не положительным.
42

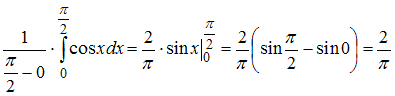
![]() на
отрезке
на
отрезке
![]() вычисляется
по формуле:
вычисляется
по формуле:
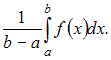 Тогда:
Тогда:
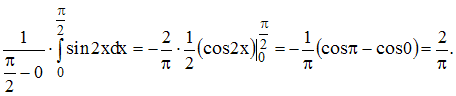
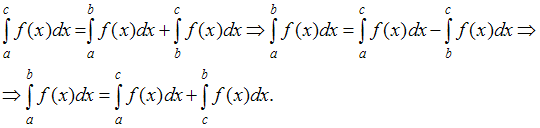 Замечание.
Свойство аддитивности интеграла
справедливо для точки
,
расположенной как внутри отрезка
,
так и вне этого отрезка, при условии
интегрируемости функции на соответствующих
отрезках.
Замечание.
Свойство аддитивности интеграла
справедливо для точки
,
расположенной как внутри отрезка
,
так и вне этого отрезка, при условии
интегрируемости функции на соответствующих
отрезках. неотрицательно.
неотрицательно.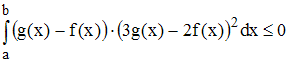 и
тоже является не положительным.
и
тоже является не положительным.
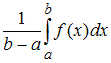 .
.
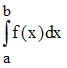 можно
представить в виде …
можно
представить в виде …
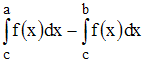
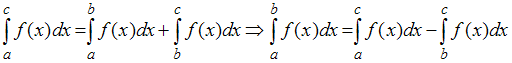 .
.
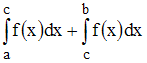
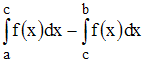
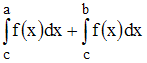
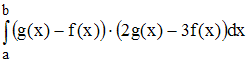 …
…
 …
…