
Приложения дифференциального исчисления фоп
-
Задание N 3.
График функции
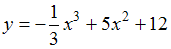 обращён
выпуклостью вверх на промежутке …
обращён
выпуклостью вверх на промежутке …
Варианты ответа:
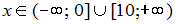
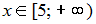
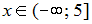
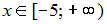
Решение:
Область
определения данной функции – вся
числовая прямая.
Исследование
проведём с помощью достаточного признака
выпуклости. Если на отрезке
![]() функция
функция
![]() непрерывна
и внутри него вторая производная
непрерывна
и внутри него вторая производная
![]() ,
то её график обращён на этом отрезке
выпуклостью вверх.
Найдём производную
второго порядка функции:
,
то её график обращён на этом отрезке
выпуклостью вверх.
Найдём производную
второго порядка функции:
![]() ,
,
![]() .
Решим неравенство:
.
Решим неравенство:
![]() .
Следовательно, график функции обращён
выпуклостью вверх на промежутке
.
.
Следовательно, график функции обращён
выпуклостью вверх на промежутке
.
-
Задание N 4.
Промежутки вогнутости (выпуклости вниз) графика функции
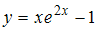 имеют
вид …
имеют
вид …
Варианты ответа:
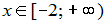
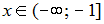
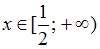

Решение:
Область
определения данной функции – вся
числовая прямая. Исследование проведем
с помощью достаточного признака
вогнутости (выпуклости вниз). Функция
![]() вогнута
на промежутке, если ее вторая производная
положительна всюду на этом промежутке.
Найдем производную второго порядка
функции:
вогнута
на промежутке, если ее вторая производная
положительна всюду на этом промежутке.
Найдем производную второго порядка
функции:
![]() ,
,
![]() .
Решим неравенство:
.
Решим неравенство:
![]() .
Учитывая, что
.
Учитывая, что
![]() ,
получим
,
получим
![]() и
и
![]() .
Следовательно, график функции выпуклый
вниз на промежутке
.
.
Следовательно, график функции выпуклый
вниз на промежутке
.
-
Задание N 4.
Минимум функции
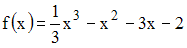 равен
…
равен
…
Варианты ответа:
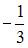
– 2
3
– 11
Решение:
Точками
экстремума непрерывной функции являются
те критические точки, при переходе через
которые меняется знак первой производной
функции (первое достаточное условие
экстремума).
Область определения
данной функции – вся числовая
прямая.
Найдем критические точки
функции:
![]() .
Исследование характера этих критических
точек можно провести с помощью первого
достаточного условия экстремума.
Найденные точки разбивают область
определения функции на промежутки, на
каждом из которых производная сохраняет
знак. Методом «пробной точки» определим
знак производной в каждом из полученных
промежутков:
.
Исследование характера этих критических
точек можно провести с помощью первого
достаточного условия экстремума.
Найденные точки разбивают область
определения функции на промежутки, на
каждом из которых производная сохраняет
знак. Методом «пробной точки» определим
знак производной в каждом из полученных
промежутков:
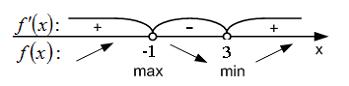 Тогда
в силу первого достаточного условия
экстремума
Тогда
в силу первого достаточного условия
экстремума
![]() –
точка минимума функции. Следовательно,
минимум функции равен:
–
точка минимума функции. Следовательно,
минимум функции равен:
![]() .
.
-
Задание N 4.
Сумма наибольшего и наименьшего значений функции
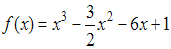 на
отрезке
на
отрезке
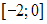 равна
…
равна
…
Варианты ответа:
6
0
3,5
- 4,5

Решение:
Данная
функция непрерывна на всей числовой
прямой, а значит, и на данном отрезке.
Как известно, такая функция достигает
своего наибольшего и наименьшего
значений либо на концах отрезка, либо
внутри него.
Используя производную
1-го порядка, найдем критические точки
функции на интервале
![]() :
:
![]() ;
;
![]() .
Точка
.
Точка
![]() не
принадлежит рассматриваемому промежутку.
Вычислим значения функции в критической
точке и на концах отрезка:
не
принадлежит рассматриваемому промежутку.
Вычислим значения функции в критической
точке и на концах отрезка:
![]() ;
;
![]() ;
;
![]() .
Из
полученных значений выбираем наибольшее
и наименьшее.
Таким образом, наибольшее
значение функции на данном отрезке
.
Из
полученных значений выбираем наибольшее
и наименьшее.
Таким образом, наибольшее
значение функции на данном отрезке
![]() ,
а наименьшее значение функции на отрезке
,
а наименьшее значение функции на отрезке
![]() .
Следователь, сумма наибольшего и
наименьшего значений функции на отрезке
равна 3,5.
.
Следователь, сумма наибольшего и
наименьшего значений функции на отрезке
равна 3,5.
-
Задание N 4.
Материальная точка движется прямолинейно по закону
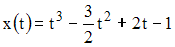 .
Тогда скорость точки в момент времени
.
Тогда скорость точки в момент времени
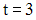 равна
…
равна
…
Варианты ответа:
18,5
Ответ неверный!

Скорость движения точки
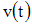 определяется
как производная от пути
определяется
как производная от пути
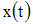 по
времени:
по
времени:
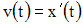 .
Тогда её скорость в момент времени
равна
.
Тогда её скорость в момент времени
равна
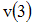 .
.
20
19
Ответ неверный!
Скорость движения точки определяется как производная от пути по времени: . Тогда её скорость в момент времени равна .
11
Ответ неверный!
Скорость движения точки определяется как производная от пути по времени: . Тогда её скорость в момент времени равна .
|
|||||||||||||||||
|
|
||||||||||||||||
|
|||||||||||||||||
|
|
||||||||||||||||
Решение:
Функция убывает на промежутке, если ее производная отрицательна всюду на этом промежутке, за исключением конечного числа точек, в которых функция непрерывна. А так как на рисунке изображен график производной функции, то таких промежутков два. Следовательно, функция убывает на промежутках: .

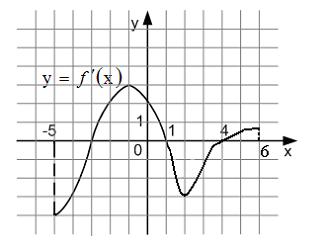 Тогда
функция
убывает
на промежутке …
Тогда
функция
убывает
на промежутке …