Дифференциальное и интегральное исчисление Область определения функции
-
Задание N 1.
Область определения функции
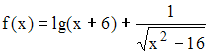имеет
вид …
Варианты ответа:
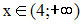
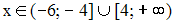
Решение:
Данная
функция определена, если определено
каждое слагаемое в отдельности. Общая
часть этих областей определения и будет
областью определения функции. Первое
слагаемое определено, если выражение,
стоящее под знаком логарифма, положительно,
для второго слагаемого необходимо,
чтобы подкоренное выражение было
неотрицательно и знаменатель дроби не
равен нулю. То есть необходимо решить
систему неравенств:
-
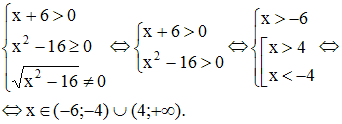
Задание N 1.
Область определения функции
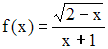имеет
вид …
Варианты ответа:
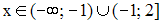
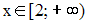
Решение:
Данная
функция определена, если одновременно
определены числитель и знаменатель
функции. Общая часть этих областей
определения и будет областью определения
функции. Числитель определен, если
подкоренное выражение неотрицательно,
а знаменатель функции не равен нулю. То
есть необходимо решить систему
неравенств:
.
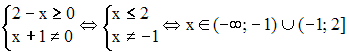Предел функции
-
Задание N 2.
Предел
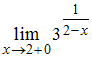равен
…
Варианты ответа:
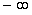
1
0
Решение:
Если
,
то есть при
справа,
выражение
и
,
то есть стремится к нулю, оставаясь
больше нуля.
Следовательно,
и
.
-
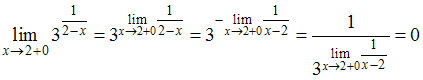Задание N 1.
Предел
равен
…
Варианты ответа:
0
3
– 2
Решение:
В
заданном пределе имеет место
неопределённость
.
В этом случае можно в числителе и
знаменателе вынести за скобку x в высшей
степени или числитель и знаменатель
разделить почленно на
,
где n – степень многочлена в знаменателе:
-
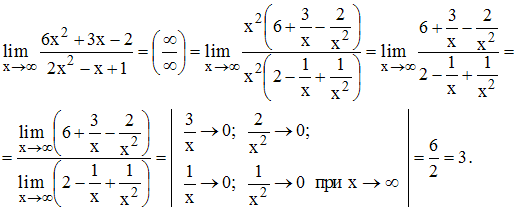
Задание N 1.
Предел
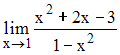равен
…
Варианты ответа:
0
2
– 1
– 2
Решение:
.
-
Задание N 2.
Предел
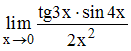равен
…
Варианты ответа:
6
0,5
0
Решение:
Здесь
имеем неопределенность вида
.
Подобного рода пределы можно вычислить
с помощью первого замечательного предела
и его следствий. При этом удобно применять
эквивалентные бесконечно малые функции:
.
-
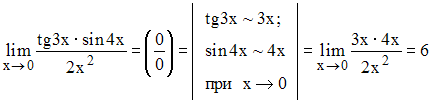Задание N 1.
Предел
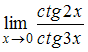равен
…
Варианты ответа:
0
1,5
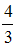
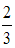
Решение:
В
заданном пределе имеем неопределённость
.
В этом случае предел можно вычислить с
помощью первого замечательного предела
и его следствий. При этом удобно применять
эквивалентные бесконечно малые функции:
.
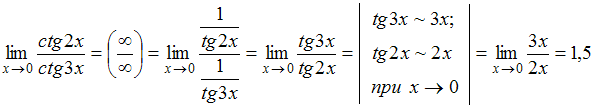