1

Пусть функция определена на отрезке . Разобьем отрезок на произвольных частей точками

В каждом из полученных частичных отрезков выберем произвольное точку («кси и-тое») . Через обозначим разность , которую будем называть длиной частичного отрезка .

Составим сумму , (1)

которую назовем интегральной суммой для функции на , соответствующей данному разбиению на частичные отрезки и данному выбору промежуточных точек .

Геометрический смысл суммы очевиден: сумма площадей прямоугольников с основаниями и высотами , если .

Определение. Если существует конечный предел интегральной суммы (1) при , не зависящий не от способа разбиения отрезка , ни от выбора точек , то этот предел называется определенным интегралом от функции по отрезку и обозначается: .

2

Свойства определенного интеграла.

1. При перестановке пределов интегрирования определённый интеграл меняет знак:

2. Определённый интеграл с равными пределами равен нулю: .

3. Для любых трех чисел , и справедливо равенство:

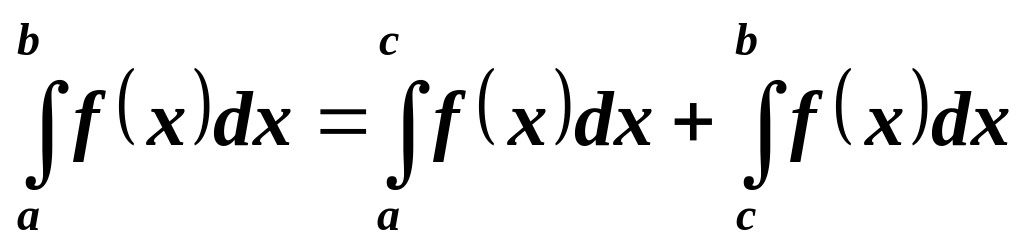
4. Постоянный множитель можно выносить за знак определенного интеграла:

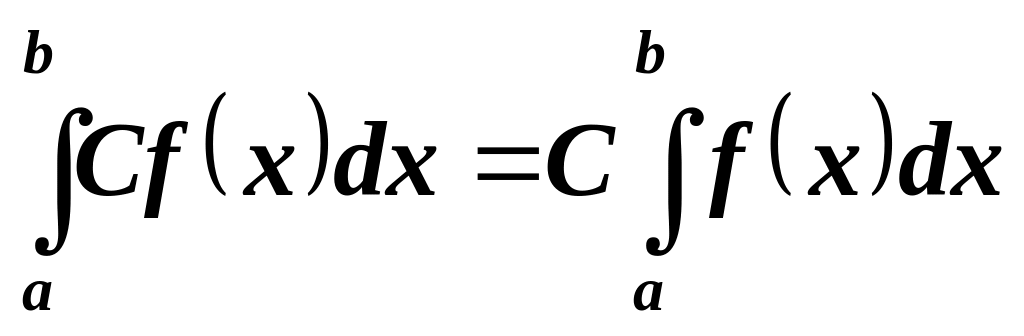
5. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов этих функций:

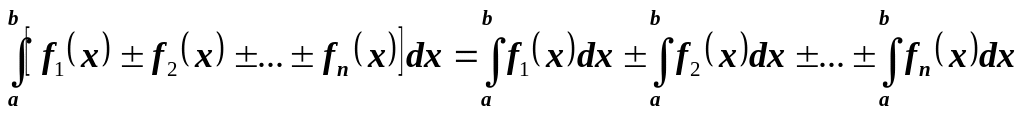
6. Пусть в каждой точке отрезка выполняется неравенство , тогда .

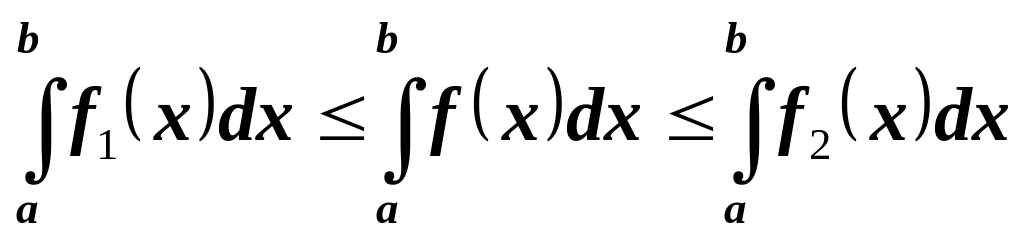3

Теорема о среднем. Если функция непрерывна на отрезке , то на нем найдется такая точка , что справедливо равенство: 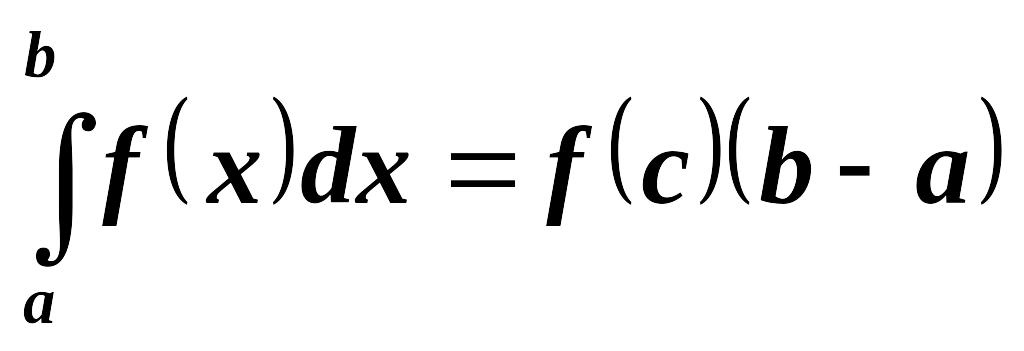, . Геометрический смысл этого утверждения состоит в том, что для площади, ограниченной кривой , осью и двумя прямыми и , можно найти равновеликий ей прямоугольник с тем же основанием и с высотой, равной одной из ординат кривой на отрезке . Отметим, что называется средним значением функции на отрезке .

4

интеграл с переменным верхним пределом представляет собой функцию своего верхнего предела. Таким образом, если мы имеем интеграл с постоянным нижним пределом и переменным верхним пределом , то величина этого интеграла будет функцией верхнего предела . Обозначим эту функцию через , т.е. положим и назовем ее определенным интегралом с переменным верхним пределом. Геометрически функция представляет собой площадь заштрихованной криволинейной трапеции

Формула Ньютона-Лейбница.

любая непрерывная на отрезке функция имеет на этом отрезке первообразные, причем одной из них является функция .

Пусть - любая другая первообразная для функции на том же отрезке . Т.к. первообразные отличаются друг от друга на постоянную (по теореме 1), то имеет место равенство

,

Подставляя в это равенство значение , и используя свойство 2 определенного интеграла, будем иметь: , т.е. имеем .

Полагая , получим - формула Ньютона-Лейбница. (2)

Разность иногда условно записывают или и тогда формула принимает вид: .

5

Замена переменной в определенном интеграле.

Теорема 3. Пусть - непрерывная функция на отрезке . Тогда, если:

1. функция дифференцируема на и непрерывна на ,

2. множеством значений функции является отрезок

3. , ,

то справедлива формула (3)- формула замены переменной в определенном интеграле.

6

. Площади плоских фигур.

1.1. Если функция неотрицательна на отрезке , то площадь криволинейной трапеции, ограниченной кривой и прямыми , , , численно равна определенному интегралу от на данном отрезке: (5) (геометрический смысл определенного интеграла).

Если верхняя ограничивающая линия фигуры задана параметрически: где , , , то площадь фигуры вычисляется по формуле: (6).

1.2. Если функция неположительна на отрезке , то площадь криволинейной трапеции, ограниченной кривой и прямыми , , , численно равна определенному интегралу от на данном отрезке, взятому со знаком «минус»: (7).

1.3. Если на отрезке , то площадь фигуры, заключенной между кривыми и на этом отрезке определяется формулой

(8).

2. Длина дуги кривой.

Длина дуги кривой , заключенной между точками с абсциссами и , определяется по формуле: (9).

Объемы тел вращения.

Если функция знакопостоянна на отрезке , то объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями , , и , вычисляется по формуле (11Аналогично, объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями , , и , вычисляется по формуле (12).

7

Определение. Пусть функция определена на полуинтервале и интегрируема в любой его части . Несобственным интегралом первого рода называется предел функции при , т.е.

(13)

Если предел, стоящий в правой части равенства (13), существует и конечен, то соответствующий несобственный интеграл называется сходящимся, в противном случае расходящимся.

Аналогично, по определению,

(14)

(15)

причем последний интеграл называется сходящимся, если сходятся оба несобственных интеграла в правой части равенства.

8

Определение. Пусть функция определена в промежутке . Точку будем называть особой, если функция не ограничена в окрестности этой точки, но ограничена на любом отрезке . Предполагается, что на любом функция интегрируема. Тогда, как бы ни было мало , если существует конечный предел , то его называют несобственным интегралом второго рода и обозначают

(16)

Если предел, стоящий в правой части выражения (16) существует и конечен, то говорят, что интеграл называется сходящимся, в противном случае – расходящимся.

Аналогично, если точка - особая точка, то несобственный интеграл в этом случае определяется так .

Если функция неограниченна в окрестности какой-нибудь внутренней точки отрезка , то по определению полагают при условии существовании обоих интегралов в правой части равенства.

Если и - особые точки, то в этом случае несобственный интеграл определяется как сумма , где - любая точка интервала, при условии существовании обоих интегралов в правой части равенства.

9