Тема: Теоремы сложения и умножения вероятностей

На стеллаже были выставлены 10-томное собрание сочинений Пушкина, три тома Дюма и 5 томов Лермонтова. Посетитель библиотеки наугад выбирает один из томов. Вероятность выбора произведения классика русской литературы равна …

Решение: Событие, состоящее в появлении хотя бы одного из событий и , называется суммой событий и . Вероятность суммы двух несовместных событий и вычисляется согласно формуле: . Рассмотрим событие – наугад выбрано произведение классика русской литературы. Это может произойти в случае выбора тома Пушкина или книги Лермонтова. Пусть событие состоит в том, что выбрано произведение Пушкина, а событие состоит в том, что выбрано произведение Лермонтова. На полке книг. Таким образом, событие является суммой событий и . Согласно условию, произведения Пушкина составляют 10 книг из 18, а Лермонтова – 5 книг из 18. Поэтому , . События и являются несовместными, поскольку среди книг не было сборников произведений различных авторов. Тогда искомая вероятность равна:

Тема: Числовые характеристики случайных величин

Случайная величина задана законом распределения 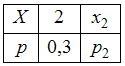. Ее математическое ожидание равно . Тогда значение равно …

Решение: Согласно определению, математическим ожиданием случайной величины с законом распределения 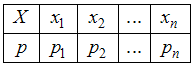называется число . Из условия имеем: , то есть . Подставив в формулу для расчета математического ожидания случайной величины данные задачи, получим: . Отсюда .

Тема: Числовые характеристики случайных величин

Математическое ожидание случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью, равно …

			4
			16
			8
			1

Решение: Согласно определению, математическим ожиданием случайной величины с законом распределения называется число . Составим закон распределения случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью (допустим, ): 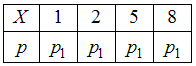. Для определения значения воспользуемся формулой: . В нашем случае . Отсюда , то есть . Таким образом, закон распределения случайной величины имеет вид: . Математическое ожидание случайной величины равно .

Тема: Числовые характеристики случайных величин

Математическое ожидание дискретной случайной величины X, заданной законом распределения 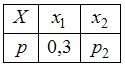, где  равно  Тогда значение  равно …

			– 1
			1
			0
			– 2

Решение: Согласно определению, математическим ожиданием случайной величины X  с законом распределения называется число Значение  найдем из условия  то есть  отсюда Кроме того, учтем, что Подставив в формулу для расчета математического ожидания случайной величины X  данные задачи, получим: Отсюда  В итоге имеем: