Тема: Классическое определение вероятности

Бросают 2 игральные кости. Вероятность того, что выпадет не менее 11 очков, равна …

Решение: Вероятностью события называется отношение числа элементарных исходов , благоприятствующих данному событию, к числу равновозможных элементарных исходов испытания: . Из определения следует, что необходимо подсчитать число событий, благоприятных данному событию, и число равновозможных элементарных исходов. Вычислим число благоприятных исходов. При броске 2 игральных костей может выпасть не менее 11 очков, то есть выпадет 11 или 12 очков. Это возможно в следующих случаях: когда на 2 костях одновременно выпадет по 6 очков (всего 12 очков), когда на первой кости выпадет 5 очков, а на второй – 6 (всего 11 очков) или когда на первой кости выпадет 6 очков, а на второй – 5 (всего 11 очков). Следовательно, . Общее число элементарных исходов определим, исходя из следующих рассуждений. Пусть на первой кости выпало 1 очко. На второй может выпасть 1, 2, 3, 4, 5 или 6 очков. Таким образом, для каждой выпавшей грани одной игральной кости может выпасть одна из 6 граней на другой. Поэтому общее число исходов определяется формулой: . Итак, .

Тема: Классическое определение вероятности

В стопке из 16 конвертов на 7 приклеены марки. Наудачу извлекают 2 конверта. Вероятность того, что на них не будет марок, равна …

Решение: Вероятностью события называется отношение числа элементарных исходов , благоприятствующих данному событию, к числу равновозможных элементарных исходов испытания: . В данной задаче событие состоит в том, что из стопки конвертов выбраны наудачу два конверта без марок. Конвертов, которые не имеют марок, штук. Вычислим . Определим, сколькими способами можно извлечь два конверта без марок ( ) из девяти имеющихся ( ). В этом нам поможет формула для нахождения числа сочетаний из элементов по : . Имеем 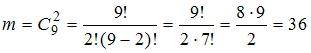. Теперь найдем . Определим, сколькими способами можно взять два конверта ( ) из имеющихся шестнадцати ( ). Получим . Используя полученные значения, найдем вероятность события : .

Тема: Теорема сложения и умножения вероятностей

Вероятность поражения цели при выстреле для первого стрелка равна 0,4, а для второго – 0,5. Тогда вероятность того, что цель будет поражена после выстрелов обоих стрелков, равна …

			0,7
			0,9
			0,2
			0,1

Решение: Рассмотрим событие – «цель поражена». Это значит, что хотя бы один из стрелков поразил цель. Таким образом, данное событие представляет собой сумму событий  и , где событие – «первый стрелок поразил цель», событие  – «второй стрелок поразил цель». Напомним, что суммой  двух событий  и  называется событие, состоящее в появлении хотя бы одного из событий  или , то есть или события , или события , или обоих этих событий. Данные события являются совместными и независимыми, то есть они могут произойти одновременно (оба стрелка при выстреле могут поразить цель), и появление события  не влияет на появление события  (поражение цели первым стрелком не влияет на результат выстрела второго стрелка). Поэтому, согласно теореме о сумме вероятностей для совместных событий, имеем: . Следовательно, .