Тема: Классическое определение вероятности

В урне 5 красных и 7 зеленых шаров. Из урны наудачу берут два шара. Вероятность того, что шары разноцветные, равна …

Решение: Вероятностью события называется отношение числа элементарных исходов , благоприятствующих данному событию, к числу равновозможных элементарных исходов испытания: . В данной задаче событие состоит в том, что из урны взяты два разноцветных шара, то есть 1 красный и 1 зеленый. Вычислим . Определим, сколькими способами можно взять 1 красный и 1 зеленый шар из имеющихся. Существует 5 способов извлечения красного шара и 7 способов извлечения зеленого шара. Для каждого извлеченного красного шара существует 7 способов извлечения зеленого шара. Поэтому общее число способов, которыми можно извлечь 2 шара разных цветов, равно . Теперь найдем . Определим, сколькими способами можно взять два шара ( ) из имеющихся двенадцати шаров ( ). В этом нам поможет формула для нахождения числа сочетаний из элементов по : 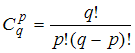. Получим 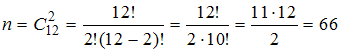. Используя полученные значения, найдем вероятность события : .

Тема: Классическое определение вероятности

Студент забыл номер аудитории, в которой проходит занятие. Он помнит только, что номер содержит три различных цифры, наибольшая из которых равна 5, а наименьшая равна 3. Вероятность того, что при случайном выборе он войдет в нужную дверь, равна …

Решение: Вероятностью события  называется отношение числа элементарных исходов , благоприятствующих данному событию, к числу  равновозможных элементарных исходов испытания: . Из определения следует, что необходимо подсчитать число исходов, благоприятных данному событию, и число равновозможных элементарных исходов. Очевидно, что благоприятное событие только одно, поскольку аудитория определена однозначно, то есть . Общее число элементарных исходов – это количество чисел, которые можно составить из 3 различных неповторяющихся цифр. Поскольку номер содержит три различных цифры, наибольшая из которых равна 5, а наименьшая равна 3, то эти цифры: 3, 4 и 5. Используем формулу для подсчета перестановок . Таких чисел . Тогда вероятность того, что при случайном выборе будет найдена необходимая аудитория, равна

Тема: Классическое определение вероятности

В урне 30 разноцветных шаров. Вероятность извлечь наугад один синий шар равна 0,6. Тогда количество синих шаров в урне равно …

			18
			5
			12
			50

Решение: Вспомним определение вероятности. Вероятностью события называется отношение числа элементарных исходов , благоприятствующих данному событию, к числу равновозможных элементарных исходов испытания: . Событие состоит в том, что из урны извлечен синий шар. Вероятность этого события . Общее число равновозможных элементарных исходов равно количеству шаров в урне, то есть . Из определения вероятности получаем . Откуда . Мы получили число элементарных исходов испытания, благоприятствующих событию , то есть количество синих шаров в урне. Следовательно, в урне 18 синих шаров.