Сложение колебаний с кратными частотами. 

Если складываемые колебания имеют резко отличающиеся частоты, то результирующее колебание даже приблизительно не будет гармоническим. В случае, если частоты складываемых колебаний кратны, т.е. w₁/w₂ = n₁/n₂ (n₁ и n₂ - целые числа), то результирующее колебание не является гармоническим, но будет периодическим. Период колебания равен наименьшему кратному периодов исходных колебаний. 

Например, если Т₁ = 2 с, Т₁ = 3 с, то Т = 6 с.

Биения. 

Пусть частоты двух скалярных колебаний не равны друг другу и w₁> w₂. Сначала рассмотрим случай, когда разность частот складываемых колебаний мала, т.е. w₁ - w₂ = W << w₁, w₂.

x₁ =  A₁·cos (w₁·t + f₁); x₂ =  A₂·cos (w₂·t + f₂).

Найдем результирующее колебание x = x₁ + x₂. Заменив величину w₁ на w₂ +W, запишем уравнение 1-го колебания в виде:

x₁ =  A₁·cos (w₂·t + (W·t+ f₁)) = = A₁·cos (w₂·t + y(t)).

В

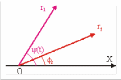
Рис. 9.7

Рис. 9.6

еличину y(t) будем рассматривать как медленно изменяющуюся во времени фазу y(t) = W·t+ f₁. Таким образом, вектор r₁ участвует в двух вращениях с частотами w₂ и W. Изобразим r₁ и r₂ на векторной диаграмме, исходящими из одной точки O. Не будем рассматривать их синхронного вращения с частотой w₂, т.к. оно не изменяет со временем их взаимного расположения этих векторов (см. рис. 9.7). Поэтому вектор r₂ будем считать  неподвижным, а r₁ - вращающимся со скоростью W относительно точки O. При вращении r₂ вектор r₁ составляет с ним некоторый угол, изменяющийся со временем. В результате сложения r₁ и r₂ получим вектор, длина которого периодически меняется со временем от значения, равного сумме A₁ + A₂, до значения, равного разности A₁ - A₂. Действительно, из (9.4) следует, что:

A² = A₁² + A₂² + 2A₁·A₂·cos(W·t + Df),    (9.6) где Dj = f₁ - f_2.

Из (9.6) видно, что амплитуда результирующего колебания А изменяется по гармоническому закону с частотой W. Период изменения амплитуды равенТ_б = 2p/W. 

Периодическое изменение амплитуды результирующего колебания, являющегося результатом сложения скалярных гармонических колебаний с близкими частотами, называется биением. 

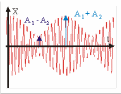
Рис. 9.8

График биения будет иметь вид, представленный на рис. 9. 8. Видно, что результирующее колебание не является гармоническим.

Пример. Если два камертона заставить звучать с близкими частотами, то в результате сложения колебаний громкость звука, обусловленная амплитудой суммарного колебания, периодически меняется с частотой биений. Высота же звука существенно не меняется, т.к. она определяется частотой результирующего колебания, которая близка к частотам складываемых колебаний. Метод биений является чувствительным методом обнаружения разницы частот.

Сложение ортогональных колебаний с равными частотами.

Рассмотрим два векторных колебания, описываемых уравнениями:

r₁ = A₁·cos(w₁·t + f₁); r₂ = A₂·cos(w₂·t + f₂).

Заметим, что с течением времени направление векторов не изменяется, а изменяется только их амплитуда. Очевидно также, что вектор A₁ параллеленr₁, а вектор A₂ параллелен r₂. Задача: найти r = r₁ + r₂. Рассмотрим только случай взаимно-перпендикулярных колебаний.

Вдоль вектора r₁ направим ось Х, вдоль r₂ - ось Y. Очевидно, результирующий вектор r перемещается в плоскости XY. Кривая, описываемая концом вектора r, называется фигурой Лиссажу. Эта фигура вписывается в четырехугольник со сторонами 2·A₁ и 2·A₂, а ее вид зависит от соотношения частот, фаз и амплитуд складываемых колебаний. 

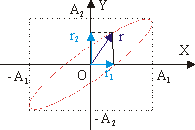
Рис. 9.9. Рис. 9.10.

Рассмотрим случай синхронных взаимно-перпендикулярных колебаний (см. рис. 9.9):

r₁ = A₁·cos (w·t + f₁);     (9.7) r₂ = A₂·cos (w·t + f₂).     (9.8)

Спроецировав уравнения (9.7) и (9.8) на оси координат и проведя суммирование проекций, получим:

x = A₁·cos (w·t + f₁);     (9.9) y = A₂·cos (w·t + f₂).     (9.10)

Исключив с помощью тригонометрических преобразований t из (9.9) и (9.10), получим математическое выражение фигуры Лиссажу, которое представляет собой уравнение эллипса:

. (9.11)

Вид эллипса определяется величиной сдвига фаз Df. В общем случае, когдаDf отлична от 0, полуоси эллипса повернуты относительно осей X и Y на определенный угол.

Рис. 9.11

Если сдвиг фаз Df = 0, то как следует из уравнения (9.11) будет справедливо следующее выражение:

(х/А₁ - y/A₂)² = 0 или y = А₂·x/А₁.

Т.е. фигура Лиссажу представляет из себя прямую линию с углом наклона aк оси X (tg a = А₂/А₁). Если Df = p, то y = - А₂·x/А₁.

Если Df = p/2, то имеем классическое уравнение эллипса, полуоси которого параллельны осям координат:

х²/А₁² + y²/A₂² = 1.

Если Df = p/2 и А₁ = А₂ = A, то эллипс превращается в окружность радиусаA.

Фигу́ры Лиссажу́ 

  Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или   вырождаются в отрезки прямых, а при разности фаз   и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

Математическое выражение для кривой Лиссажу

где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз

Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид прямой (A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a/b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.

Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и

являются полиномами Чебышева первого рода степени N.

Примеры

a = 1, b = 2 (1:2) a = 3, b = 2 (3:2) a = 3, b = 4 (3:4) a = 5, b = 4 (5:4) a = 9, b = 8 (9:8)

X. Доплер (1803—1853) — австрийский физик, математик и астроном.

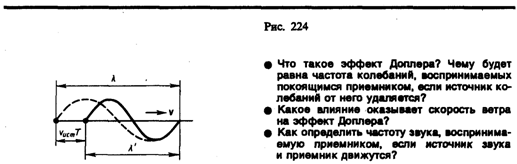
Для рассмотрения эффекта Доплера предположим, что источник и приемник звука движутся вдоль соединяющей их прямой; v_ист и v_пр — соответственно скорости движения источника и приемника, причем они положительны, если источник (приемник) приближается к приемнику (источнику), и отрицательны, если удаляется. Частота колебаний источника равна v₀.

1. Источник и приемник покоятся относительно среды, т. е. v_ист = v_пр=0. Если v — скорость распространения звуковой волны в рассматриваемой среде, то длина волны l=vT=v/v₀. Распространяясь в среде, волна достигнет приемника и вызовет колебания его звукочувствительного элемента с частотой

Следовательно, частота v звука, которую зарегистрирует приемник, равна частоте v₀, с которой звуковая волна излучается источником.

2. Приемник приближается к источнику, а источник покоится, т. е. v_пр>0, v_ист=0. В данном случае скорость распространения волны относительно приемника станет равной v + v_пр. Так как длина волны при этом не меняется, то

т. е. частота колебаний, воспринимаемых приемником, в (v+v_пр)/v раз больше частоты колебаний источника.

3. Источник приближается к преемнику, а приемник покоится, т. е. v_ист >0, v_пр=0.

Скорость распространения колебаний зависит лишь от свойств среды, поэтому за время, равное периоду колебаний источника, излученная им волна пройдет в направле­нии к приемнику расстояние vT (равное длине волны l) независимо от того, движется ли источник или покоится. За это же время источник пройдет в направлении волны расстояние v_истT (рис. 224), т. е. длина волны в направлении движения сократится и станет равной l'=l—v_истТ=(v—v_ист)T, тогда

т. е. частота n колебаний, воспринимаемых приемником, увеличится в v/(v – v_ист) раз. В случаях 2 и 3, если v_ист<0 и v_пр<0, знак будет обратным.

4. Источник и приемник движутся относительно друг друга. Используя результаты, полученные для случаев 2 и 3, можно записать выражение для частоты колебаний, воспринимаемых приемником:

                                                                      (159.1)

причем верхний знак берется, если при движении источника или приемника происходит их сближение, нижний знак — в случае их взаимного удаления.

Из приведенных формул следует, что эффект Доплера различен в зависимости от того, движется ли источник или приемник. Если направления скоростей v_пр и v_ист не совпадают с проходящей через источник и приемник прямой, то вместо этих скоростей в формуле (159.1) надо брать их проекции на направление этой прямой.