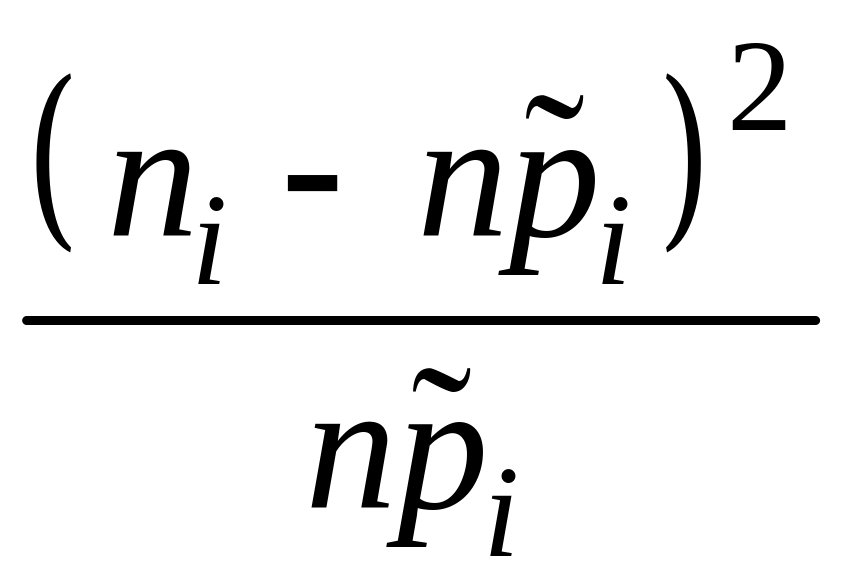3 Перевірка статистичних гіпотез про закон розподілу випадкової величини
3.1 Мета завдання
Вивчити критерії згоди, навчитися перевіряти гіпотези про закон розподілу випадкової величини за допомогою критеріїв Пірсона і Колмогорова при аналізі статистичних даних.
3.2 Методичні вказівки з організації самостійної роботи студентів
Попередньою вимогою для виконання завдання є засвоєння таких теоретичних знань: статистичні гіпотези, нульова та конкуруюча гіпотези, статистичний критерій перевірки нульової гіпотези, значення критерію, що спостерігається, критична область, критичні точки, двостороння та одностороння критичні області, критерії Пірсона, Колмогорова.
3.3 Основні положення
У загальній постановці задача перевірки статистичних гіпотез про закони розподілу випадкової величини X формулюється в такий спосіб.
За
результатами спостережень отримана
статистична оцінка закону розподілу
випадкової величини X
у вигляді емпіричної функції розподілу
.
Формулюється статистична гіпотеза
,
яка полягає в тому, що закон розподілу
досліджуваної випадкової величини X
має вигляд
.
Для перевірки цієї статистичної гіпотези
розглядається статистика критерію U,
що характеризує міру неузгодженості
між теоретичною (запропонованою за
гіпотезою
) та емпіричною функціями
розподілу. Обравши статистику критерію,
робимо оцінку її закону розподілу і для
заданого рівня значимості
будуємо критичну область.
Якщо вибіркове значення статистики знаходиться поза критичною областю, то гіпотеза, що перевіряється, приймається, якщо ж статистика належить критичній області, то гіпотеза про закон розподілу випадкової величини X відхиляється.
Під
час використання критерію Пірсона за
міру неузгодженості U
гіпотетичного й емпіричного розподілів
приймається величина
,
обчислена за
такою формулою:
,
(3.1)
де k – число інтервалів;
– частота потрапляння в інтервал i;
– ймовірність потрапляння випадкової
величини X
в інтервал i,
обчислена за гіпотетичним розподілом
з заміною невідомих параметрів розподілу
їхніми оцінками;
n – обсяг вибірки.
Для
нормального закону розподілу ймовірність
потрапляння випадкової величини X
в інтервал
визначається в такий засіб:
,
(3.2)
де
– функція Лапласа, значення якої наведені
в табл. В.1.
Для показового розподілу ймовірність потрапляння випадкової величини X в інтервал визначається за формулою:
,
(3.3)
а для рівномірного розподілу – за формулою:
.
(3.4)
Величина , обчислена за формулою (3.1) , при n®¥ має розподіл " – квадрат" із l=k-r-1 ступенями свободи, де r – число невідомих параметрів теоретичного розподілу , визначених за вибіркою. Причому, для нормального розподілу r=2, для показового – r=1 , а для рівномірного – r=2.
Процедура перевірки статистичної гіпотези про закон розподілу зводиться до такого.
Для
заданого рівня значущості
і
числа ступенів свободи
за табл. B.3
визначають критичну точку
,
що визначає нижню межу критичної області.
За
вибіркою, використовуючи формулу (3.1),
розраховують значення
критерію, що спостерігається.
Якщо > – гіпотеза відхиляється; якщо < – приймається, тобто вважається, що результати вибіркового обстеження не суперечать висунутій гіпотезі.
Для оцінки закону розподілу неперервної випадкової величини X у випадку, коли теоретичний закон розподілу визначений із точністю до параметрів розподілу, може бути використаний критерій Колмогорова.
За міру неузгодженості використовується статистика вигляду:
,
(3.5)
де
– верхня грань модуля різниці емпіричної
і теоретичної
функцій розподілу,
n – об'єм
вибірки, тобто
;
(3.6)
Розраховане
за формулою (3.5) значення статистики
порівнюється з критичною точкою
,
отриманою з табл. В.4 для заданого рівня
значущості
.
Якщо
>
– гіпотеза
відхиляється, якщо
<
– приймається. Це означає, що гіпотетична
функція розподілу
узгоджується з даними спостережень.
Існує
наближене правило застосування критерію
Колмогорова, відповідно до якого гіпотеза
приймається, якщо
<
1.
3.3 Приклади виконання завдання
Приклад 3.1 Даний приклад є продовженням прикладів 1.1, 2.1.
Для вибірки реалізації випадкової величини (табл. 1.2) перевірити висунуту в завданні 1 гіпотезу про нормальний закон розподілу, використовуючи критерії згоди Пірсона і Колмогорова.
Розв'язок
Продовжуємо досліджувати випадкову величину, задану табл. 1.2. Перевіримо висунуту в завданні 1 гіпотезу про нормальний закон розподілу заданої випадкової величини, використовуючи критерії згоди Пірсона. Для цього побудуємо табл. 3.1, де значення ймовірностей влучення випадкової величини в певний інтервал обчислюються за формулою (3.2), частоти влучення в інтервал задані в табл. 1.3.
Таблиця 3.1 – Таблиця
для розрахунку
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
-0,97 |
0,765 |
|
-1,7055 |
-0,5 |
-0,456 |
0,044 |
0,032 |
2 |
0,765 |
2,5 |
-1,7055 |
-1,13362 |
-0,456 |
-0,372 |
0,084 |
0,042 |
3 |
2,5 |
4,235 |
-1,13362 |
-0,561743 |
-0,372 |
-0,213 |
0,159 |
0,067 |
4 |
4,235 |
5,97 |
-0,561743 |
0,010136 |
-0,213 |
0,004 |
0,217 |
0,324 |
5 |
5,97 |
7,705 |
0,010136 |
0,582015 |
0,004 |
0,220 |
0,216 |
0,653 |
6 |
7,705 |
9,44 |
0,582015 |
1,15389 |
0,220 |
0,376 |
0,156 |
0,009 |
7 |
9,44 |
11,175 |
1,15389 |
1,72577 |
0,376 |
0,458 |
0,082 |
0,024 |
8 |
11,175 |
12,91 |
1,72577 |
|
0,458 |
0,5 |
0,042 |
0,281 |
|
1 |
1,432 |
||||||
Сума
елементів 9-го стовпчика дає значення
критерію, що спостерігається
.
Для заданого рівня значущості
та числа ступенів свободи
за табл. B.3 визначають критичну точку
.
Оскільки
,
вважатимемо, що немає підстав відхиляти
гіпотезу про нормальний закон розподілу
генеральної сукупності, тобто результати
вибіркового обстеження не суперечать
висунутій гіпотезі про нормальний закон
розподілу випадкової величини.
Перевіримо висунуту в завданні 1 гіпотезу про нормальний закон розподілу заданої випадкової величини, використовуючи критерії згоди Колмогорова. Для цього використаємо формули (3.5), (3.6).
Для
обчислення
побудуємо табл. 3.2.
Таблиця 3.2
– Таблиця для розрахунку
-
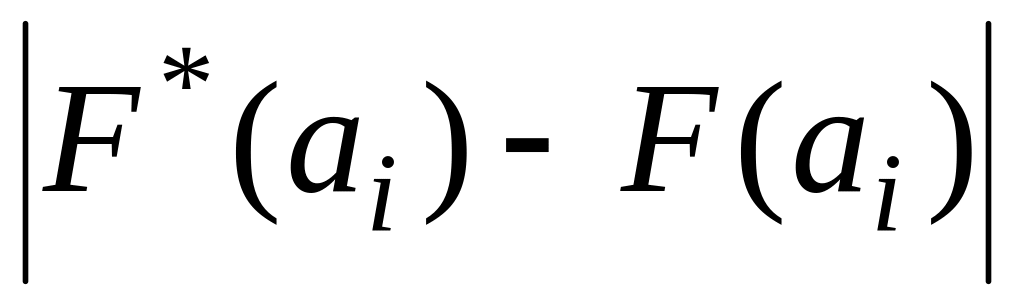
-0,97
0
0,01
0,01
0,765
0,05
0,04
0,01
2,5
0,125
0,13
0,005
4,235
0,3
0,29
0,01
5,97
0,475
0,5
0,025
7,705
0,75
0,72
0,03
9,44
0,9
0,87
0,03
11,175
0,975
0,96
0,015
12,91
1
0,99
0,01
Знайдемо
.
Обчислимо значення критерію
.
Використовуючи табл. В.4, знайдемо
критичну точку розподілу Колмогорова
.
Оскільки
,
немає підстав відхиляти гіпотезу про
нормальний закон розподілу, що збігається
з перевіркою за критерієм
Пірсона.
Приклад 3.2. Даний приклад є продовженням прикладів 1.2, 2.2.
Для вибірки реалізації випадкової величини (табл. 1.5) перевірити висунуту в завданні 1 гіпотезу про показовий закон розподілу, використовуючи критерії згоди Пірсона і Колмогорова.
Розв'язок
Продовжуємо досліджувати випадкову величину, задану табл. 1.5. Перевіримо висунуту в завданні 1 гіпотезу про показниковий закон розподілу заданої випадкової величини, використовуючи критерії згоди Пірсона Для цього побудуємо табл. 3.3, де значення ймовірностей потрапляння випадкової величини в певний інтервал обчислюються за формулою (3.3).
Таблиця 3.3 – Таблиця для розрахунку
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
0,02 |
0,721 |
-0,020 |
-0,708 |
0,981 |
0,493 |
0,488 |
51 |
0,099 |
2 |
0,721 |
1,422 |
-0,708 |
-1,397 |
0,493 |
0,247 |
0,245 |
27 |
0,252 |
3 |
1,422 |
2,123 |
-1,397 |
-2,085 |
0,247 |
0,124 |
0,123 |
12 |
0,008 |
4 |
2,123 |
2,824 |
-2,085 |
-2,773 |
0,124 |
0,062 |
0,062 |
3 |
1,641 |
5 |
2,824 |
3,525 |
-2,773 |
-3,462 |
0,062 |
0,031 |
0,031 |
1 |
1,429 |
6 |
3,525 |
4,226 |
-3,462 |
-4,150 |
0,031 |
0,016 |
0,016 |
4 |
3,811 |
7 |
4,226 |
4,927 |
-4,150 |
-4,839 |
0,016 |
0,008 |
0,008 |
0 |
0,784 |
8 |
4,927 |
5,628 |
-4,839 |
-5,527 |
0,008 |
0,004 |
0,004 |
1 |
0,933 |
9 |
5,628 |
6,329 |
-5,527 |
-6,216 |
0,004 |
0,002 |
0,002 |
0 |
0,198 |
10 |
6,329 |
7,03 |
-6,216 |
-6,904 |
0,002 |
0,001 |
0,001 |
1 |
8,159 |
|
17,314 |
||||||||
Сума
елементів 10-го стовпчика дає значення
критерію, що спостерігається
.
Для заданого рівня значимості
та числа ступенів свободи
за табл. B.3 визначають критичну точку
.
Оскільки
,
вважатимемо, що гіпотеза про показовий
закон розподілу генеральної сукупності
відхиляється при рівні значимості
.
Для рівня значимості
та числа ступенів свободи
критична точка дорівнює
.
Оскільки
,
вважатимемо, що гіпотеза про показниковий
закон розподілу генеральної сукупності
приймається при рівні значущості
.
Перевіримо висунуту в завданні 1 гіпотезу про показовий закон розподілу заданої випадкової величини, використовуючи критерії згоди Колмогорова. Для цього використаємо формули (3.5), (3.6).
Для обчислення побудуємо табл. 3.4.
Таблиця 3.4 – Таблиця для розрахунку
-
0,02
0
0,019
0,019
0,721
0,51
0,507
0,003
1,422
0,78
0,753
0,027
2,123
0,90
0,876
0,024
2,824
0,93
0,938
0,008
3,525
0,94
0,969
0,029
4,226
0,98
0,984
0,004
4,927
0,98
0,992
0,012
5,628
0,99
0,996
0,006
6,329
0,99
0,998
0,008
7,03
1,0
0,999
0,001
Знайдемо
.
Обчислимо значення критерію
.
Використовуючи табл. В.4, знайдемо
критичну точку розподілу Колмогорова
.
Оскільки
,
немає підстав відхиляти гіпотезу про
показниковий закон розподілу, що не
збігається з перевіркою за критерієм
Пірсона при рівні значущості
.
При рівні значимості
критична точка дорівнює
,
,
гіпотеза про показниковий закон розподілу
генеральної сукупності приймається,
що збігається з перевіркою за критерієм
Пірсона при рівні значимості
.
Приклад 3.3. Даний приклад є продовженням прикладів 1.3, 2.3.
Для вибірки реалізації випадкової величини (табл. 1.8) перевірити висунуту в завданні 1 гіпотезу про рівномірний закон розподілу, використовуючи критерії згоди Пірсона і Колмогорова.
Розв'язок
Продовжуємо досліджувати випадкову величину, задану табл. 1.8. Перевіримо висунуту в завданні 1 гіпотезу про рівномірний закон розподілу заданої випадкової величини, використовуючи критерії згоди Пірсона. Для цього побудуємо табл. 3.5, де значення ймовірностей потрапляння випадкової величини в певний інтервал обчислюються за формулою (3.5).
Таблиця 3.5 – Таблиця для розрахунку
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
0,18 |
1,051 |
0,1 |
11 |
0,1 |
2 |
1,051 |
1,922 |
0,1 |
12 |
0,4 |
3 |
1,922 |
2,793 |
0,1 |
8 |
0,4 |
4 |
2,793 |
3,664 |
0,1 |
12 |
0,4 |
5 |
3,664 |
4,535 |
0,1 |
10 |
0 |
6 |
4,535 |
5,406 |
0,1 |
9 |
0,1 |
7 |
5,406 |
6,277 |
0,1 |
8 |
0,4 |
8 |
6,277 |
7,148 |
0,1 |
8 |
0,4 |
9 |
7,148 |
8,019 |
0,1 |
11 |
0,1 |
10 |
8,019 |
8,89 |
0,1 |
11 |
0,1 |
|
2,4 |
||||
Сума
елементів 6-го стовпчика дає значення
критерію, що спостерігається
.
Для заданого рівня значимості
та числа ступенів свободи
за табл.
B.3 визначають критичну точку
.
Оскільки
,
вважатимемо, що при рівні значимості
немає підстав відхиляти гіпотезу про
рівномірний закон розподілу генеральної
сукупності, тобто результати вибіркового
обстеження не суперечать висунутій
гіпотезі про рівномірний закон розподілу
випадкової величини.
Перевіримо висунуту в завданні 1 гіпотезу про рівномірний закон розподілу заданої випадкової величини, використовуючи критерії згоди Колмогорова. Для цього використаємо формули (3.5), (3.6).
Для обчислення побудуємо табл. 3.6.
Таблиця 3.6 – Таблиця для розрахунку
-
0,18
0
0
0
1,051
0,11
0,1
0,01
1,922
0,23
0,2
0,03
2,793
0,31
0,3
0,01
3,664
0,43
0,4
0,03
4,535
0,53
0,5
0,03
5,406
0,62
0,6
0,02
6,277
0,7
0,7
0
7,148
0,78
0,8
0,02
8,019
0,89
0,9
0,01
8,89
1,0
1,0
0
Знайдемо
.
Обчислимо значення критерію
.
Використовуючи табл. В.4, знайдемо
критичну точку розподілу Колмогорова
.
Оскільки
,
немає підстав відхиляти гіпотезу про
рівномірний закон розподілу, що
збігається з перевіркою за критерієм
Пірсона при рівні значущості
.
3.6 Зміст звіту
Звіт має містити: мету завдання, гіпотезу про закон розподілу заданої випадкової величини, основні розрахункові формули, результати обчислень за цими формулами, необхідні висновки про перевірку гіпотез про закон розподілу заданої випадкової величини.
3.7 Індивідуальні завдання
Вивчити критерії згоди Пірсона і Колмогорова та порядок використання їх під час перевірки гіпотез про закон розподілу випадкової величини.
Виписати
розрахункові формули і зробити необхідні
обчислення для одержання
і
.
Для заданого рівня значущості
=0.05
за табл.
В.3 і В.4 визначити
і
.
Перевірити гіпотези про закон розподілу досліджуваної випадкової величини X, використовуючи критерії згоди Пірсона і Колмогорова, та зробити висновок про можливість його застосування.
Дані для виконання завдання вміщені в табл. А.1.
3.8 Контрольні запитання
1. У чому полягає задача статистичної перевірки гіпотез про закони розподілу випадкової величини?
2. Яка статистика приймається за міру неузгодженості між теоретичними й емпіричними законами розподілу під час використання критерію Пірсона?
3. Який порядок перевірки статистичних гіпотез про закон розподілу під час використання критерію Пірсона?
4. Яка статистика приймається за міру неузгодженості між теоретичними й емпіричними законами розподілу під час використання критерію Колмогорова?
5. Який порядок перевірки статистичних гіпотез про закон розподілу під час використання критерію Колмогорова?