Решение:

5. В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: . Здесь , где ,  и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для водорода ( ) число i равно …

			7
			5
			3
			6

Решение: Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная , а на каждую колебательную степень – . Средняя кинетическая энергия молекулы равна: . Здесь – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: , где  – число степеней свободы поступательного движения, равное 3;  – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;  – число степеней свободы колебательного движения, минимальное количество которых равно 1. Для водорода ( ) (двухатомной молекулы) ,  и . Следовательно,

6. Газ занимает объем 5 л под давлением 2 МПа. При этом кинетическая энергия поступательного движения всех его молекул равна …

Решение: Согласно уравнению кинетической теории для давления идеального газа (основному уравнению МКТ идеальных газов), произведение давления идеального газа и его объема равно двум третям энергии поступательного движения всех его молекул: . Отсюда

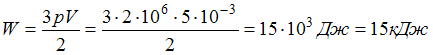
7. Если не учитывать колебательные движения в молекуле водорода при температуре 200 К, то кинетическая энергия в (Дж) всех молекул в 4 г водорода равна …

Решение: Средняя кинетическая энергия одной молекулы равна: , где  – постоянная Больцмана, – термодинамическая температура;  – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы . Молекула водорода  имеет 3 поступательные и 2 вращательные степени свободы, следовательно,  В 4 г водорода содержится  молекул, где масса газа, молярная масса водорода, число Авогадро. Кинетическая энергия всех молекул будет равна:

8. Отношение средней кинетической энергии вращательного движения к средней энергии молекулы с жесткой связью . Это имеет место для …

			водорода
			водяного пара
			гелия
			метана ( )

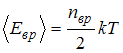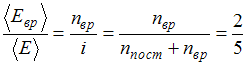Решение: Средняя кинетическая энергия молекулы равна: , где  – постоянная Больцмана, – термодинамическая температура,  – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: . Средняя энергия вращательного движения . Таким образом, с учетом того что связь атомов в молекуле по условию является жесткой (в этом случае ), отношение . Отсюда , что имеет место для газов с двухатомными и многоатомными линейными молекулами. Следовательно, это – водород.