10.10. Производные сложной функции
Теорема
10.17.
Пусть функция
дифференцируема в точке
,
функции
и
- в точке
,
причем
,
.
Тогда сложная функция
дифференцируема в точке
и имеют место равенства
,
.
Доказательство. Рассмотрим приращение сложной функции в точке .
.
Преобразуем приращение с помощью равенств
,
,
которые
запишем в виде
,
.
Тогда
.
В силу дифференцируемости функции в точке имеем представление
,
где
функции
,
стремятся к нулю при
и
.
Поскольку функции
и
непрерывны в точке
,
то при
и
верно
и
.
Тогда
,
стремятся к нулю и при
и
.
В силу дифференцируемости функций и в точке справедливы представления
,
с
функциями
,
стремящимися к нулю при
и
.
Тогда
.
В
полученном представлении приращения
величины
и
стремятся к нулю при
и
.
Поэтому сложная функция
является дифференцируемой в точке
по определению.
При
приращения
,
,
можно понизать как частные приращения
по переменной
.
Поэтому имеем равенство
.
Поделим это равенство на и найдем предел правой части полученного равенства при :
.
Предел правой части существует. Тогда существует предел левой части и
.
Аналогично устанавливается вторая формула утверждения теоремы.
Теорема доказана.
Рассмотрим частные случаи сложной функции.
1)
Пусть
,
и в некоторой области изменения переменных
и
определена сложная функция
.
Функция
дифференцируема в точке
,
а функция
- в точке
.
Тогда справедливы формулы
,
.
2)
Пусть
,
,
и в некоторой области изменения переменных
и
определена сложная функция
.
Функции
и
дифференцируемы соответственно в точках
и
,
а функция
- в точке
,
где
,
.
Тогда
,
.
3)
Пусть
,
,
и в некотором промежутке изменения
переменной
определена сложная функция
.
Функции
и
дифференцируемы в точке
,
а функция
- в точке
,
где
,
.
Тогда производная сложной функции может
быть вычислена по формуле
.
Пример. Применим последнюю формулу для нахождения производной функции, имеющей сложное выражение:
.
Можно
записать, что
,
если положить:
,
.
Имеем:
,
,
,
.
Теперь применим формулу третьего частного случая:
.
10.11. Дифференциалы высших порядков функции нескольких переменных
Пусть
в каждой точке
области
функция
дифференцируема и
.
Зафиксируем приращения
и
.
Тогда дифференциал
есть функция двух переменных. Если эта
функция дифференцируема, то можно
вычислить ее дифференциал
,
который называется дифференциалом
второго порядка функции
в точке
.
Применимы так же краткие обозначения:
,
.
Формула
для дифференциала второго порядка
выводится с использованием свойств
дифференциала. Предположим, что
производные
,
непрерывны в точке
.
Тогда
.
И с учетом равенства смешанных производных получаем:
.
Пример.
Найти дифференциал второго порядка
функции
в произвольной точке
его существования и в точке
.
Найдем частные производные второго порядка данной функции.
,
,
.
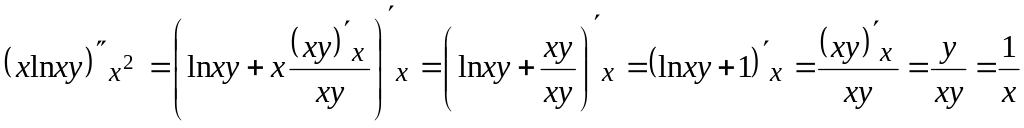Теперь, применив формулу для второго дифференциала, получаем:
.
Вычислив значения частных производных в точке , будем иметь:
.
По определению
есть
дифференциал
- го порядка функции
в точке
.
Для существования дифференциала
в точке
,
например, достаточно существования в
некоторой окрестности точки
частных производных
- го порядка и непрерывности их в точке
.
Для функций двух переменных справедлива формула
.
К
примеру, для
с применением этой формулы получаем:
.