10.14. Производная по направлению. Градиент

Рассмотрим характеристики функций нескольких переменных.

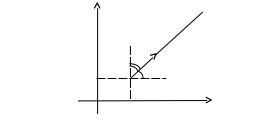
Пусть функция определена в некоторой окрестности точки (см. рисунок 10.9) и дифференцируема в этой точке. Обозначим через луч с началом в точке , который ориентирован вектором , - единичный вектор. Запишем параметрические уравнения луча :

Рисунок 10.9

Точка принадлежит лучу . Длина отрезка луча равна

.

Функцию , принимающую значения в точках луча, можно определить как функцию одного аргумента . Производная этой функции в точке называется производной функции в точке по направлению вектора и обозначается символами

, .

По определению имеем:

.

Поскольку

,

то

и представляет собой скорость изменения функции в точке по направлению вектора .

Формулу для вычисления производной по направлению получим с применением формулы теоремы о производных сложной функции (третий частный случай).

.

Таким образом,

.

По определению градиентом функции в точке является вектор

.

С применением формулы для производной по направлению и скалярного произведения выясним смысл градиента (необходимые обозначения приведены на рисунке 10.10).

.

Рисунок 10.10

При значение будет наибольшим и равным 1. При этом производная по направлению принимает наибольшее значение . Следовательно, вектор определяет направление наибольшего роста функции в точке , а есть скорость наибольшего роста.

В случае функции трех переменных, определенной в окрестности точки (см. рисунок 10.11) и дифференцируемой в этой точке, производной в точке по направлению вектора с направляющими косинусами является величина

.

Для вычисления производной применяется формула

.

По определению вектор

есть градиент функции в точке . В случае имеет место формула

.

Рисунок 10.11

Пример. Найти производную функции в точке по направлению вектора , , и градиент в точке .

Полагая , вычислим значения частных производных заданной функции в точке .

.

Найдем направляющие косинусы вектора .

, , .

Тогда с применением формулы для производной по направлению получаем

.

Искомым градиентом будет вектор .

С использование правил дифференцирования, формул для производной сложной функции устанавливаются следующие свойства градиента. Предполагаем, что функции и дифференцируемы в точке .

а) ;

б) ;

в) , если ;

г) для сложной функции имеет место формула

,

где .