8.7.3. Рекурсия в графике
Если в состав PROLOG-системы входит модуль GRAPH, то знакомиться с рекурсией удобно на примере простейших графических построений. Общее правило построения N рисунков можно сформулировать так:
рекурсивное правило: чтобы нарисовать N рисунков, надо уметь нарисовать N 1 рисунок и знать, как рисуется N-я картинка.
граничное правило: надо знать, как рисуется первый рисунок.
Примеры
8.9. Изобразить на экране 20 точек, расположенных в одной строке на расстоянии 10 пикселей друг от друга. Первая точка имеет координаты (50, 50). Пусть граф-драйвер находится в текущем каталоге.
clauses
init if initgraph(0,0,_,_,” ”).
ris(1) if putpixel(50,50,15),!.
ris(N) if M=N1,ris(M),X=50+20+M,putpixel (X, 50, 15).
rez if init,ris(20),readln(_),closegraph.
goal
rez.
8.10. Построить 15 концентрических окружностей с центром в точке (300, 200) с радиусами, отличающимися друг от друга на 10 пикселей. Внутренняя окружность имеет R = 10.
clauses
konz(1) if circle(300,200,10)!.
konz(N) if M=N1,konz(M),R=10+M*10,
circle(300,200,R).
goal
initgraph(0,0,_,_,””),konz(15),readln(_),
closegraph.
8.11. Выполнить рисование каждой из окружностей случайно выбранным цветом.
clauses
zwet(c) if c=random(15),setcolor(c).
konz(1) if zwet(c),circle(300,200,10),!.
konz(N,c) if M=N1,konz(M),zwet(c),k=10+M *10,circle(300,200,R).
goal
initgraph (0,0,_,_,””),konc(15,c).
8.12. Нарисовать 4 расположенные друг под другом окружности.
predicates
image_item (integer)
query
clauses
image_item (0) if !.
image_item (N) if
Y = N * 100 – 50,
circle (50, Y, 40),
M = N – 1,
image_item (M).
query if
initgraph (0, 0, _, _, ""),
cleardevice,
setcolor (15),
image_item (4),
readln (_),
closegraph.
goal
query.
Упражнения
Написать программу с внутренней целью, которая рисует в графическом режиме один из представленных ниже рисунков, используя рекурсивный вызов предиката, рисующего отдельные повторяющиеся части изображения:
8.8. Списки prolog. Рекурсивная обработка списков
8.8.1. Определение и структура списка
Мы приводили рекурсивное определение списка в 8.2. Повторим его:
пустой список [ ] это список;
[A¦B] список, если В список, то есть список это упорядоченная последовательность элементов. Это определение требует ясного понимания структуры списка.
Рассмотрим несколько вариантов записи списка:
[1 ¦ [2, 3, 4]] здесь 1 голова списка, а [2, 3, 4] хвост списка, который сам обязательно является списком и может быть в свою очередь разбит на голову и хвост. Получается следующего вида дерево (рис. 8.2).
Рис. 8.2. Пример представления списка [1 ¦ [2, 3, 4]]
[1, 2, 3, 4]. Здесь нет явно выраженной головы и хвоста списка. По умолчанию PROLOG-система положит голову равной 1, но программой может в качестве головы использовать список [1, 2]. Тогда исходный список может быть записан в виде [[1, 2]; [3, 4]]. Возможны следующие представления этого списка (рис. 8.3).
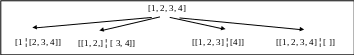
Рис. 8.3. Представления списка [1, 2, 3, 4]
Не подлежит расщеплению только пустой список. У него нет ни головы, ни хвоста. Списки широко используются для представления деревьев синтаксического разбора, грамматик, карт, графов и т.д. Заметим, что есть языки, например LISP, где списки являются единственным способом представления данных. На PROLOG список это частный вид структуры.