8.10. Задачи, использующие структуру графа
Графом называется совокупность вершин и ребер, соединяющих эти вершины (рис. 8.4).
Рис. 8.4. Граф
На этом рисунке изображен граф, состоящий из 6 вершин М1,…,М6 и 5 ребер a, b, c, d, e. Одна из вершин М6 – изолированная. Граф может быть ориентированным (если на ребрах указано направление) или неориентированным (в противном случае).
Примеры
8.25. Поиск в лабиринте.
В доме 6 комнат b, c, d, e, f, g, сведения о том, где находятся двери, представлены в виде фактов: дверь(b,e), дверь(b,c), дверь(d,e), дверь(c,d), дверь(e,f), дверь(g,e). В комнате g есть телефон. Эти связи могут быть изображены в виде графа (рис. 8.5):
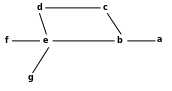
Рис. 8.5. К условию примера 8.25
Задача состоит в том, чтобы путник нашел в лабиринте ту комнату, в которой находится телефон, поскольку ему срочно надо позвонить, причем нельзя дважды заходить в одну комнату.
У этой задачи могут быть варианты: путник, блуждая по лабиринту, ищет выход из него.
Введем координаты перехода (X,Y,T), который истинен, если можно перейти из комнаты Х в комнату Y, имея список Т пройденных комнат. Тогда грамотное условие рекурсивности поиска может быть записано так:
переход (Х,Х,Т) if !.
/* всегда можно перейти из Х в Х, оставаясь в ней*/
Рекурсивное правило сформулируем так: выбираем смежную с Х комнату Z и дописываем Z в список Т. Получится:
переход (X,Y,T) if дверь (X,Z), not (принадлежит (Z,T)), переход (Z,Y , [Z¦T] ).
Но кроме варианта дверь(X,Z) нас устроит вариант дверь(Z,X). Поэтому к имеющемуся рекурсивному правилу следует добавить:
переход (X,Y,T) if дверь(Z,X), not (принадлежит(Z,T)), переход (Z, Y, [Z¦T]).
Для завершения задачи следует ввести факт, ограничивающий процесс поиска, например: телефон есть в комнате g; или сокровище находится в комнате е и т.д. Если факт есть телефон(g) введен в БД, то вопрос можно задать так:
Переход (a,X,[ ]), есть_телефон(Х).
Постарайтесь сформулировать вопросы самостоятельно.
Упражнения
Нарисовать конверт (рис. 8.6), не отрывая карандаша от бумаги и не проводя 2 раза по одной и той же линии. Результат – список пройденных ребер графа.
Рис. 8.6. К условию упражнения 8.154
Имеется база данных о дорогах между 5-ю городами. Определить, как можно проехать из одного заданного пункта в другой.
Дана база данных дороги (X,Y,расстояние). Определить самый короткий путь из заданного пункта в другой.
Определить, в какие города можно уехать из пункта Р, если в БД задана сеть дорог. Определить, в какие города нельзя доехать из пункта Р.
Определить, есть ли в БД "дороги" (X,Y) пункт, который соединен со всеми остальными.
Определить, является ли система дорог звез
дой
(рис. 8.7).
Рис. 8.7. К условию упражнения 8.159
Пять городов соединены телефоном только попарно. В каждом городе живет книголюб, имеющий ранние издания двух редких книг. Определить, может ли книголюб из заданного пункта обменяться книгами с книголюбом из другого города? Если да, то через какие города?
Рис. 8.8. К условию упражнения 8.160
Телефонная сеть между 6 городами оплачена так:
сеть(X,Y,стоимость 1-ой минуты).
Определить, можно ли позвонить из пункта 12 в пункт 14 и сколько будет стоить 1 минута разговора, если стоимости складываются при сложении путей.
Имеется 4 города, расстояния между которыми известны. Требуется проложить дорогу так, чтобы она проходила через каждый город. Вывести все возможные варианты работ и полученный километраж.
Для предыдущей задачи вывести все варианты работ, при которых километраж ≤500.
Бригада артистов должна выступить в городах N1, N2, N3, соединенных дорогами. Составить маршрут бригады, при котором длина пути была бы минимальной.
Из города N1 есть дороги в города N2, N3, N4, из которых соединены дорогой N2 и N3. Определить, можно ли послать посылку почтой из одного заданного города в другой. Если да, то по какому маршруту.