6.2. Вага тіла
Формула
сили
ваги:
= m
.
Вагу тiла можна вимiрювати на пружинних
терезах. Це вимiрювання визначає, однак,
не силу притягання тiла до Землi, а лише
ту частину
цiєї сили
,
яка проявляється статично, бо зважування
на терезах не дає змоги виявити другу
частину сили
,
яка проявляється в переносному прискореннi
ω2r
тiла, зумовленому добовим обертанням
тiла разом із Землею.
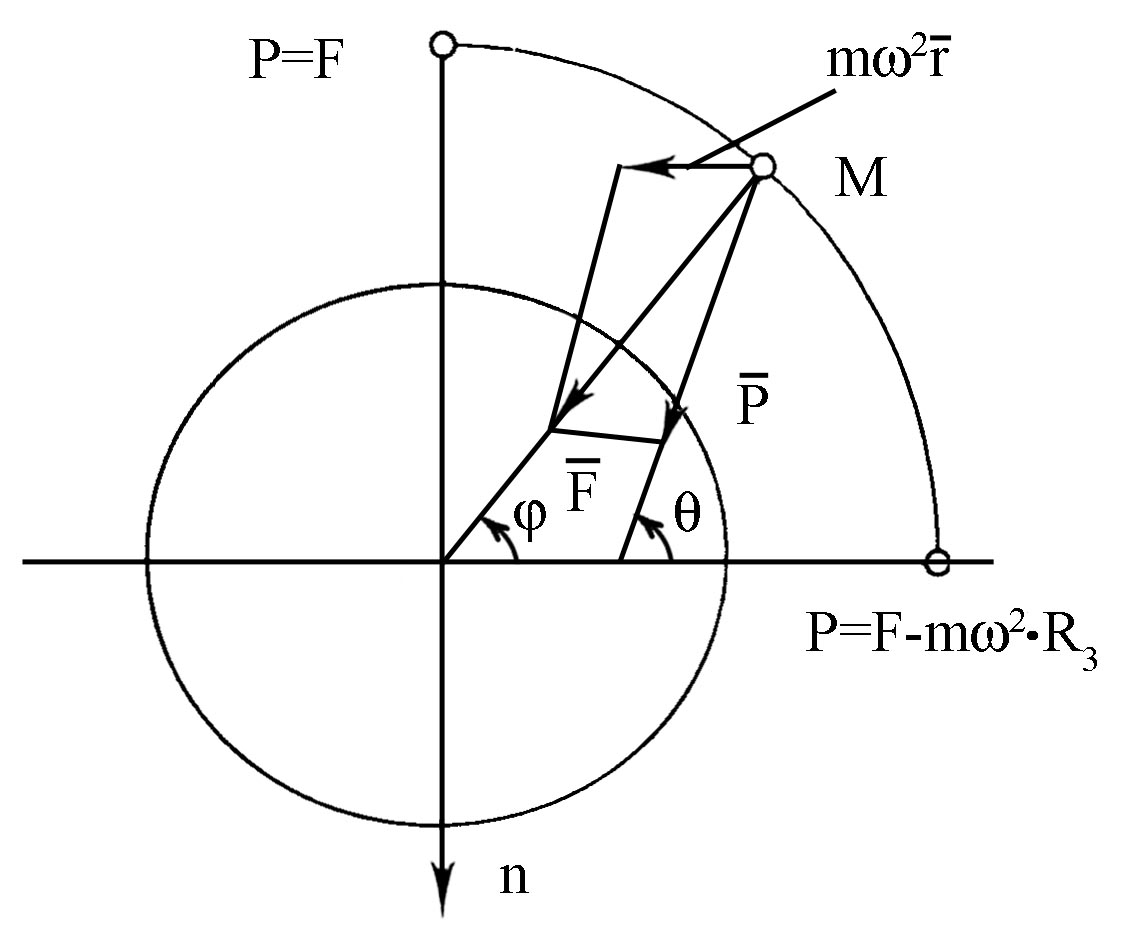
Вага тiла, згiдно з її означенням, дорiвнює:
=
m
.
(6.11)
На
полюсi доцентрова сила дорiвнює нулю i
сила ваги дорiвнює силi притягання
,
тобто
=
.
Вага тiла на екваторi найменша i дорiвнює
Р
= F
mω2Rз.
За другим законом Ньютона
= m
,
де
-
абсолютне прискорення тiла.
Значить
=
m
m
= m(
)
= m
,
(6. 12)
де позначено
= . (6.13)
Абсолютне прискорення 0 можна визначити з рiвностi
γ(mM/R32)·(
3/R3)
= m
,
(6.14)
де 3/R3 - одиничний вектор, напрямлений вiд тiла М до центра Землi;
=
γ(M/R32)·(
3/R3).
(6.15)
Значить
g2
= (g0
)2
= g02
2
g0
+
.
Оскiльки = ω2R3cosφ, то
Нехтуючи пiд радикалом останнiм доданком, що має множником ω4, i добуваючи наближено квадратний корiнь, матимемо:
g = g0 ω2R3cos2φ. (6.16)
Для полюса φ = π/2, g0 = 983 см/с2; ω2R3≈3 см/с2, а тому формулу (6.16) можна записати так:
g = (983 3cos2φ) см/с2.
Однак справжнi вимiрювання показують, що
g = (983 5,2cоs2φ) см/с2.
На практицi користуються середнiм значенням g = 981 см/с2. У зв’язку з впровадженням мiжнародної системи одиниць СI введено так зване нормальне значення g, яке позначають gн; за означенням приймають gн = 9,80665 м/с2.
6.3. Рiвняння руху вiльної матерiальної точки вiдносно Землi
Запишемо рiвняння руху матерiальної точки вiдносно Землi, користуючись поняттям ваги:
m = m 2m( ´ ), (6.17)
або, враховуючи, що m = , одержимо
m = 2m( ´ ).
Запишемо формулу сили ваги як m i, скорочуючи на m, одержимо остаточно:
= 2( ´ ). (6.18)
Це рiвняння руху вiльної матерiальної точки вiдносно Землi.
da/dt = ω1 = ωsinθ.
Знак ”мінус” тут означає, що обертання вiдбувається за стрiлкою годинника (зi сходу через пiвдень на захiд), якщо дивитися згори.