Понятие сбалансированности дерева

Мы убедились, что время выполнения всех основных операций в бинарном дереве поиска пропорционально высоте дерева. Возникает вопрос, как оно связано с количеством элементов в дереве?

В дереве высоты h может поместиться N=2^h-1 элементов. В этом случае h=O(logN). И мы получим возможность выполнять все основные операции контейнера за время O(logN), чего не было ни в каких других контейнерах.

Именно это свойство дерева называется сбалансированностью. В сбалансированном дереве на каждом шаге поиска элементов мы делим его примерно пополам, число элементов слева и справа примерно одинаково – поэтому это свойство и называют сбалансированностью.

Основными методами обеспечения сбалансированности дерева являются красно-черные деревья и AVL-деревья [5, гл. 13].

Словари

При разработке программного обеспечения часто необходимо хранить набор объектов, имеющих определенные уникальные идентификаторы. Типичные операции для этого набора – добавление элемента (с указанием идентификатора), удаление элемента по идентификатору, поиск элемента по идентификатору.

Идентификатор, по которому возможен поиск, называют ключом. Данные, которые можно найти, называют значением. Программная конструкция, которая хранит пары «ключ-значение» и обеспечивает операции добавления элемента, поиска элемента по ключу и удаления элемента по ключу, называется словарем или ассоциативным массивом.

Как технически должен реализовываться словарь? Мы имеем следующую ситуацию:

1. Желательно ускорить добавление элемента, поиск элемента по ключу, удаление элемента по ключу.

2. Ключ уникален, двух объектов с одним ключом не бывает.

3. Можно придумать для ключей какую-либо операцию сравнения. Ее всегда можно придумать – в самом крайнем случае, вспомним, что ключи состоят из битов и могут быть представлены как двоичные числа.

Решение очевидно – бинарное дерево поиска. В каждом узле бинарного дерева поиска лежат ключ и значение. Упорядочивается это бинарное дерево поиска по принципу сравнения ключей.

Пример словаря приведен на рис. 15. В этом словаре упорядоченным в лексикографическом порядке (по алфавиту как в словаре) строковым ключам сопоставлены значения, равные их длинам.

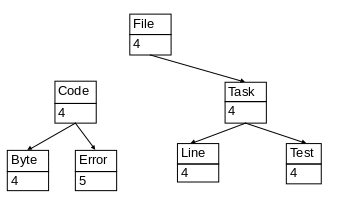
Рис. 15. Словарь.

Очереди с приоритетами

Очередь с приоритетами реализуется на базе невозрастающей пирамиды – частного случая бинарного дерева. Введем несколько необходимых понятий.

1. Назовем 0-ым уровнем дерева его корневой элемент.

2. Назовем потомков корневого элемента 1-ым уровнем дерева.

3. Назовем потомков элементов 1-ого уровня элементами 2-ого уровня.

4. Вообще назовем элементами уровня N, где 1 <= N, потомков элементов уровня N-1.

Ясно, что на уровне N существует 2^N элементов.

Введем нумерацию элементов внутри уровня по следующему принципу.

1. На уровне N элементы имеют уровень от 0 до 2^N-1.

2. На нулевом уровне единственный элемент имеет номер 0.

3. Если элемент уровня N-1 имеет (на своем уровне) номер k, то его левый потомок имеет на уровне N номер 2k, а правый потомок номер 2k+1.

Проще говоря, нумерация элементов идет слева направо. При этом номера элементов не зависят от того, есть фактически элемент в этой позиции (левого/правого потомка такого-то узла), или его нет. Реально нумеруются не элементы, а позиции в дереве, которые элементы могут занимать.

Пример распределения элементов дерева по уровням и нумерации элементов внутри уровней приведен на рис. 16.

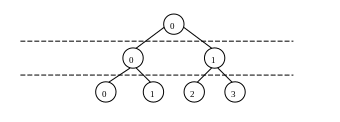
Рис. 16. Дерево. Уровни и нумерация

Пирамидой [5, гл.6] называется дерево высоты h (с уровнями от 0 до h), соответствующее следующим правилам:

1. Уровни от 0 до h-1 полностью заполнены (уровень номер k содержит 2^k элементов).

2. На уровне h заполнены элементы с номерами 0,…., M. 0 <= M <=2^h -1. Т.е. этот уровень начали заполнять слева направо и частично или полностью заполнили.

Пример пирамиды приведен на рис. 17.

Рис. 17. Пирамида.

Для пирамиды доказано, что количество узлов N в пирамиде высоты h лежит в диапазоне 2^h <= N <= 2^h+1-1. Соответственно, о высоте h мы можем сказать, что log₂N-1 <= h <= log₂N. Пирамида – это сбалансированное дерево.

Невозрастающей пирамидой называется пирамида со следующими свойствами:

1. В пирамиде хранятся значения, к которым применима операция сравнения <=.

2. Значения, хранимые в потомках данного узла, меньше либо равны значениям, хранимым в данном узле.

Примеры невозрастающей пирамиды приведены на рис. 18.

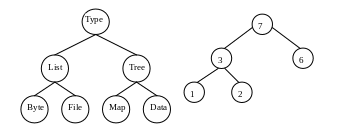
Рис. 18. Невозрастающие пирамиды.

Добавление элемента в невозрастающую пирамиду возможно за время, равное O(h)=O(logN), где h – высота пирамиды, N – количество элементов пирамиды.

Алгоритм такого добавления следующий:

1. Сначала мы должны добавить элемент в такую позицию, чтобы пирамида осталась пирамидой.

2. В этом случае в пирамиде может быть только одно нарушение правила невозрастания – вновь добавленный элемент может быть больше своего предка. Если его нет – ничего делать не надо, добавление закончено.

3. Если нарушение есть – новый элемент и его предка нужно поменять местами. Новый элемент будет гарантированно больше обоих своих потомков – и своего бывшего предка (по условию перестановки), и бывшего потомка своего бывшего предка (потому что тот меньше, чем его бывший предок).

4. После этого в пирамиде может быть только одно нарушение порядка – между поднявшимся наверх только что добавленным элементом и его бывшим предком. Если нарушения нет, операция закончена, если нарушение есть – их нужно поменять местами.

5. Мы повторяем эти действия, пока не исчезнет нарушение порядка или пока мы не дойдем до корня пирамиды.

Первый шаг может занять время 0(1) или O(h) в зависимости от деталей реализации. Далее мы делаем от 0 до h шагов, связанных с подъемом нового элемента на одну ступеньку каждый. Шаг занимает время 0(1). Нетрудно убедиться, что общее время операции будет O(h).

Удаление максимального (корневого) элемента из невозрастающей пирамиды возможно за время O(h) =O(logN).

Алгоритм такого удаления следующий:

1. Удаляя максимальный элемент, мы должны поставить на его место последний по номеру элемент последнего уровня пирамиды – чтобы наше дерево осталось пирамидой.

2. В этом случае в пирамиде может быть только одно нарушение правила невозрастания – новый корневой элемент может быть меньше одного (или обоих) своих потомков. Если нарушения нет – ничего делать не надо, добавление закончено.

3. Если нарушение есть – нужно выбрать из этих трех элементов (новый корневой и его потомки) максимум и поменять местами с корневым элементом. Это гарантированно будет максимальный элемент – все элементы 2-ого и следующих уровней меньше того элемента первого уровня, чьими прямыми или косвенными потомками являются.

4. После этого в пирамиде может быть только одно нарушение невозрастания – между только что опустившимся на уровень элементом и его потомками. Если его нет – ура. Если есть - нужно выбрать из трех элементов максимальный и поменять его местами с родительским.

5. После каждого шага у нас остается не более одного нарушения невозрастания и точка нарушения движется вниз по пирамиде на уровень за шаг.

Первый шаг может занять время 0(1) или O(h) в зависимости от деталей реализации. Далее мы делаем от 0 до h шагов, связанных с спуском элемента на одну ступеньку каждый. Шаг занимает время 0(1). Нетрудно убедиться, что общее время операции будет O(h).

Также за время O(h) можно восстановить свойство невозрастания после изменения значения одного из элементов. В этом случае очевидно, что нарушение невозрастания может быть только одно. Это нарушение с участием измененного элемента – если он уменьшился, мог стать меньше своих потомков, если увеличился – больше своего предка. В первом случае его нужно смещать вниз (так же, как корневой элемент после удаления), во втором – поднимать наверх (так же, как добавленный элемент при добавлении). Число необходимых шагов будет не больше h.

Поскольку при работе с пирамидой можно за время O(logN) добавить элемент, удалить элемент и изменить приоритет элемента, пирамида – оптимальный вариант для реализации очереди с приоритетами.

Пирамида может представляться в виде массива. В этом массиве сначала лежит корневой элемент, затем (в порядке нумерации) элементы первого уровня, далее элементы второго уровня и т.д. Пример пирамиды и ее представления в виде массива приведен на рис. 19.

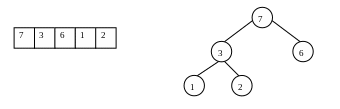
Рис. 19. Пирамида и ее представление в виде массива.

Если мы представляем пирамиду из N элементов в виде массива, то потомками элемента A[k] являются элементы A[2k], A[2k+1].

Соответственно, в невозрастающей пирамиде должны выполняться правила:

1. .

2. .

Т.е. если у элемента есть потомки, они должны соблюдать условие невозрастания.

Стеки

Стеком называется контейнер, работающий по принципу Last In – First Out. В нем возможно удаление только последнего добавленного элемента.

Стек поддерживает три операции – добавить элемент, посмотреть на последний добавленный элемент, удалить последний добавленный элемент.

Стек может быть реализован на базе различных контейнеров, т.к. многие контейнеры могут реализовать операции добавления элемента в конец, удаления последнего элемента и доступа к последнему элементу. Стек может быть эффективно построен на базе массива, двунаправленного списка, двусторонней очереди.