Сортировка Шелла
Сортировка Шелла [7] – алгоритм, использующий преимущества сортировки вставками и стремящийся избежать его недостатков. На первом этапе выбирается сравнительно большое число K и методом сортировки вставками сортируются массивы
A[0], A[K], A[2K],…
A[0], A[K], A[2K],…
…
A[K-1], A[2K-1], A[3K-1],…
После этого число K уменьшается и выполняется новая сортировка. На последнем этапе (K=1) выполняется обычная сортировка вставками, но, поскольку массив будет почти отсортированным, она будет выполнена очень быстро.
Время работы сортировки Шелла зависит от способа выбора K. Один из наиболее популярных способов выбора значений K это K=2w-1.
Сортировка шейкером
Сортировка шейкером [8] подобна сортировке пузырьком [1]. Ее отличие заключается в чередовании проходов в одну и другую сторону. На первом шаге мы идем слева направо («тонут» тяжелые элементы), на втором – справа налево («всплывают легкие»), на третьем – снова слева направо и так далее.
На шаге 0 перебираются пары элементов от “0 – 1” до “N-2 – N-1”. На шаге 1 мы знаем, что максимальный элемент уже в позиции N-1 и перебираем пары элементов от «N-3 – N-2» до «0 – 1». На шаге 2 минимальный элемент встал в позицию 0 и нужно перебирать пары элементов от «1 – 2» до «N-3 - N-2».
Сортировка шейкером иллюстрируется на рис. 1.
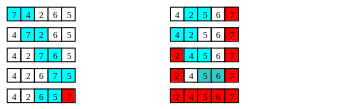
Рис. 1. Сортировка шейкером.
После двух проходов (слева направо, затем справа налево) массив оказался отсортированным. После третьего прохода мы это поняли (потому что не было перестановок) и закончили сортировку.
Сортировка расческой (Comb sort)
Сортировка расческой [9] близка к сортировке пузырьком [1]. Она также основана на проверке пар элементов и их перестановке при необходимости.
В сортировке расческой на первом этапе сравниваются пары элементов, отстоящие друг от друга на расстояние K. Как правило, выбирается K = N/1.3, т.е. немногим меньше длины массива. После того, как не останется элементов, отстоящих друг от друга на расстояние K и нарушающих порядок, величина уменьшается в фиксированное количество раз (чаще всего 1.3). Так мы продолжаем, пока K не станет равно 1. Если K=1 и при очередном проходе мы не нашли нарушений порядка – сортировка окончена.
Последний этап сортировки расческой повторяет сортировку пузырьком. Но, благодаря предыдущим этапам, оказывается достаточным очень небольшое количество проходов на последнем этапе.
Сортировка расческой по отношению к сортировке пузырьком играет примерно ту же роль, что и сортировка Шелла по отношению к сортировке вставками.
Плавная сортировка (Smooth sort)
Метод плавной сортировки [10] основан на пирамидальной сортировке. Его единственное отличие заключается в том, что он стремится минимизировать время работы в случае почти отсортированного массива.
В первую очередь метод плавной сортировки пробегает по началу массива и находит (за время O(N)) возрастающую часть массива (см. рис. 2.)
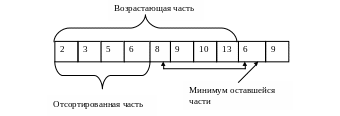
Рис. 2. Плавная сортировка.
Далее, также за время O(N), в оставшейся части массива находится ее минимум.
После этого методом бинарного поиска, за время O(logN), в возрастающей части выделяется та часть, которая должна остаться на своих местах. Это элементы, меньшие либо равные минимуму правой части. Минимум правой части должен встать сразу же за ними, поменявшись местами со следующим элементом.
После этого к оставшейся части массива применяется пирамидальная сортировка [5, гл. 6].