Оценка апостериорных вероятностей

Рассмотренные в предыдущих разделах методы можно исполь­зовать для оценки апостериорных вероятностей на основа­нииппомеченных выборок, пользуясь выборками для оценки соот­ветствующих плотностей распределения. Предположим, что мы

размещаем ячейку объема Vвокруг х и захватываемkвыборок, из которых оказываются помеченными . Тогда очевидной оценкой совместной вероятностир(х, ) будет

Таким образом, приемлемой оценкой для будет

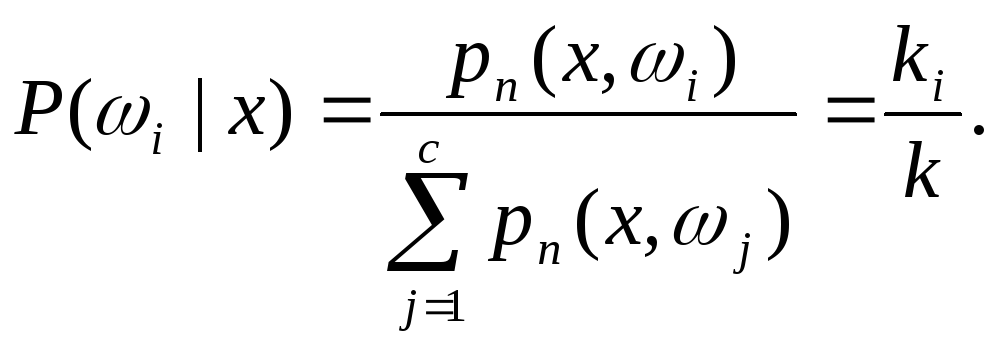
Иначе говоря, оценка апостериорной вероятности того, что состоя­ние природы есть , является просто долей выборок в ячейке, по­меченных .

Чтобы свести уровень ошибки к минимуму, мы выбираем класс, наиболее часто представляемый в ячейке. Если имеется достаточное количество выборок и если ячейка достаточно мала, то можно по­казать, что результаты будут в этом случае близки к наилучшим.

Если дело доходит до выбора размера ячейки, то можно восполь­зоваться или методом парзеновского окна, или методом ближай­ших соседей. В первом случае будет некоторой определенной функцией отп,а именно =1/.Во втором случае будет рас­ширяться до тех пор, пока не вместит некоторое определенное чис­ло выборок, а именноk=.В любом случае по мере устремленияп к бесконечности в бесконечно малую ячейку будет попадать беско­нечное число выборок. Тот факт, что объем ячейки может стать бе­сконечно малым и все же будет содержать бесконечно большое число выборок, позволяет нам изучать неизвестные вероятности с опреде­ленной точностью и, таким образом, постепенно добиваться опти­мальных результатов. Довольно интересно, как мы увидим далее, что можно получать сравнимые результаты, основывая наше реше­ние только на метке единственного ближайшего соседа величины х.

Правило ближайшего соседа Общие замечания

Пусть ={x₁, . . .,х_n} будет множествомnпомеченных выбо­рок, и пустьбудет выборкой, ближайшей к х. Тогдаправило ближайшего соседадля классификации х заключается в том, что х присваивается метка, ассоциированная с. Правило ближайшего соседа является почти оптимальной процедурой; его применение обычно приводит к уровню ошибки, превышающему минимально возможный байесовский. Как мы увидим, однако, при неограничен­ном количестве выборок уровень ошибки никогда не будет хуже бай­есовского более чем в два раза.

Прежде чем вдаваться в детали, давайте попытаемся эвристи­чески разобраться в том, почему правило ближайшего соседа дает такие хорошие результаты. Для начала отметим, что метка , ассоциированная с ближайшим соседом, является случайной вели­чиной, а вероятность того, что=, есть просто апостериорная вероятность . Когда количество выборок очень велико, следует допустить, чторасположено достаточно близко к х, чтобы . В этом случае можем рассматривать пра­вило ближайшего соседа как рандомизированное решающее правило, которое классифицирует х путем выбора класса с вероятностью . Поскольку это точная вероятность того, что природа на­ходится в состоянии , значит, правило ближайшего соседа эффек­тивно согласует вероятности с реальностью. Если мы определяем (х) как

(23)

то байесовское решающее правило всегда выбирает . Когда ве­роятность близка к единице, выбор с помощью правила ближайшего соседа почти всегда будет таким же, как и байесовский, это значит, что когда минимальная вероятность ошибки мала, то вероятность ошибки правила ближайшего соседа также мала. Когда близка к 1/с,так что все классы одинаково правдоподобны, то выборы, сделанные с помощью этих двух правил, редко бывают одинаковыми, но вероятность ошибки в обоих случаях составляет приблизительно 1-1/с.Не исключая необходимости в более тща­тельном анализе, эти замечания позволяют меньше удивляться хо­рошим результатам правила ближайшего соседа.

Наш анализ поведения правила ближайшего соседа будет направ­лен на получение условной средней вероятности ошибки Р(е|х) при большом количестве выборок, где усреднение производится по выборкам. Безусловная средняя вероятность ошибки будет найдена путем усредненияР(е|х)по всем х:

(24)

Заметим, что решающее правило Байеса минимизирует Р(e) путем минимизацииР (е|x)для каждого х.

Если Р*(е|x)является минимально возможным значениемР(e|x), а Р* —минимально возможным значениемР(е),то

(25)

и

(26)