Лекция №5

Содержание:

Обучение статистической дискриминантной функции 2

Оценка параметров и обучение с учителем 3

Введение 3

Оценка по максимуму правдоподобия 4

Общая идея метода 4

Случай многомерного нормального распределения: неизвестно среднее значение 5

Общий многомерный нормальный случай 6

Байесовский классификатор 7

Плотности, условные по классу 8

Распределение параметров 8

Обучение при восстановлении среднего значения нормальной плотности 9

Случай одной переменной: p(|) 9

Случай одной переменной: p(x|) 11

Непараметрические методы 13

Введение 13

Оценка плотности распределения 13

Парзеновские окна 15

Общие соображения 15

Сходимость среднего значения 16

Сходимость дисперсии 17

Оценка методом kn ближайших соседей 20

Оценка апостериорных вероятностей 22

Правило ближайшего соседа 23

Общие замечания 23

Сходимость при использовании метода ближайшего соседа 23

Правило k ближайших соседей 26

Обучение статистической дискриминантной функции

Формализация задачи статистической классификации и оптимизации дискриминантной функции для нормального распределения рассмотрена. Следующая задача, которая может быть для нас интересна – как определить функцию распределения вероятности. Одним из путей является аппроксимация. Предполагая это, мы хотим аппроксимировать для набора функций:

где точка надpозначает оценку.

- произвольные функции, может быть набор базисных функций. Наша задача – найти коэффициенты , так, что СКО

Всеxдля класса могут быть минимизированы. После замены будет:

Необходимое условие минимизацииQ:

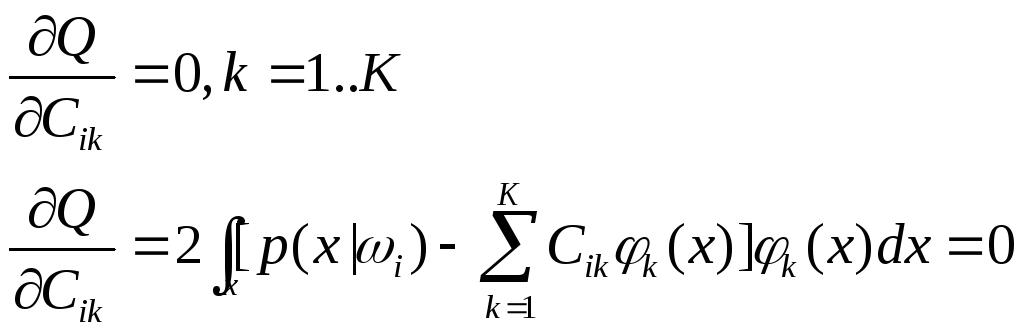
Из него :

По определению, это есть величина

НаборKлинейных равенств в для определенногоiможет быть получен решением для , но знание

необходимо. Зная, что

можно аппроксимировать так

где Ni– число выборок в классеi, затем

Это набор из Kлинейных равенств, он может быть решен дляk

Если, в частности ортонормальные функции выбраны для так, что

то

Один из коэффициентов определен,

функция плотности сформирована. Заметим, что xjзадается последовательностью.

затем можно получить итеративно из следующего выражения:

где обозначают полученные коэффициенты с

образами соответственно.

Оценка параметров и обучение с учителем Введение

В гл. 2рассматривались вопросы разработки оптимального классификатора в случае, когда известны априорные вероятности Р(ω_j) и плотностиp(x|ω_j),условные по классу. К сожалению, на практике при распознавании образов полная вероятностная струк­тура задачи в указанном смысле известна далеко не всегда. В ти­пичном случае имеется лишь неопределенное общее представление об исследуемой ситуации и некоторый наборконструктивных вы­борок —конкретных представителей образов, подлежащих класси­фикации¹. Задача, следовательно, заключается в том, чтобы найти способ построения классификатора, используя эту информацию.

Один из подходов к задаче заключается в ориентировочной оценке неизвестных вероятностей и плотностей по выборкам и по­следующем использовании полученных оценок, как если бы они были истинными значениями. Оценка априорных вероятностей в типичных задачах классификации образов не представляет большой трудности. Иначе обстоит дело с вопросом оценки условных по классу плотностей. Имеющееся количество выборок всегда пред­ставляется слишком малым для их оценки, и если размерность вектора признаков х велика, то задача сильно усложняется. Труд­ность значительно уменьшится, если возможна параметризация условных плотностей, исходя из общего представления о задаче. Допустим, например, что есть некоторые основания предпо­ложить, что p(x|ω_j) соответствует нормальному распределению со средним значением μ_jи ковариационной матрицей ∑_jхотя точные значения указанных величин неизвестны. Это упрощает задачу, сводя ее вместо определенияфункции p(x|ω_j), к оценкепараметровμ_jи ∑_j.

Задача оценки параметров, относящаяся к классическим зада­чам математической статистики, может быть решена различными способами. Мы рассмотрим два общепринятых способа —оценку по максимуму правдоподобияибайесовскую оценку.Несмотря на то, что результаты часто оказываются весьма близкими, подход к решению при применении этих способов принципиально различен. При использовании методов максимального правдоподобия зна­чения параметров предполагаются фиксированными, но неизвест­ными. Наилучшая оценка определяется как величина, при которой вероятность реально наблюдаемых выборок максимальна. При бай­есовских методах параметры рассматриваются как случайные переменные с некоторым априорно заданным распределением. Ис­ходя из результатов наблюдений выборок, это распределение пре­образуют в апостериорную плотность, используемую для уточнения имеющегося представления об истинных значениях параметров.

Как мы увидим, в байесовском случае характерным следствием привлечения добавочных выборок является заострение формы функции апостериорной плотности, подъем ее вблизи истинных значений параметров. Это явление принято называть байесовским обучением.Следует различатьобучение с учителемиобучение без учителя.Предполагается, что в обоих случаях выборки х полу­чаются посредством выбора состояния природы ω_j, с вероятностью Р(ω_j), а затем независимого выбора х в соответствии с вероятност­ным закономp(x|ω_j).Различие состоит в том, что при обучении с учителем известно состояние природы (индекс класса) для каж­дого значения, тогда как при обучении без учителя оно неизвестно. Как и следовало ожидать, задача обучения без учителя значительно сложнее. В данной главе будет рассмотрен только случай обучения с учителем, рассмотрение же случая обучения без учителя отложим до гл. 6.