
- •Вопрос 1. Классические методы оценки инвестиционных проектов.
- •Вопрос 2. Модель Гордона оценки инвестиционных проектов.
- •Вопрос 3. Применение нечеткой математики в анализе инвестиционных проектов.
- •Вопрос 4. Применение метода анализа иерархий в анализе инвестиционных процессов.
- •Вопрос 5. Применение дерева решений в анализе инвестиционных проектов.
- •Вопрос 6. Применение имитационного моделирования для прогнозирования инвестиционных процессов.
- •Вопрос 7. Применение var для оценки инвестиционных рисков.
- •Вопрос 8. Формирование портфеля ценных бумаг Марковица.
- •Вопрос 9. Формирование портфеля ценных бумаг Тобина.
- •Вопрос 10. Предпочтения потребителя и функция полезности.
- •Вопрос 11. Уравнение Слуцкого. Изменения спроса при увеличении цены с компенсацией.
- •Вопрос 12. Уравнение Слуцкого. Изменение спроса при изменении дохода.
- •Вопрос 13. Модель фирмы
- •Вопрос 14. Реакция производителя на изменение цены выпуска
- •Вопрос 15. Реакция производителя на изменение цен ресурсов.
- •Вопрос 16. Равновесие Курно
- •Вопрос 17. Равновесие и неравновесие Стакельберга
- •Вопрос 18. Виды макроэкономических производственных функций
- •Вопрос 19. Аксиоматика неоклассической производственной функции
- •Вопрос 20. Предельные характеристики функции Кобба-Дугласа
- •Глава 21. Статическая модель Леонтьева
- •Глава 22. Динамическая модель Леонтьева
- •Глава 23. Модель Неймана
- •Глава 24. Нелинейная динамическая модель Кейнса
- •Глава 25. Динамическая модель Кейнса
- •Вопрос 26. Мультипликатор, акселератор и инерционное звено
- •27. Передаточная функция и колебательное звено
Вопрос 19. Аксиоматика неоклассической производственной функции
В соответствии с неоклассической теорией экономического роста. Основным источником интенсивного развития является рост производительности, обусловленный техническим прогрессом и лучшей организацией производства. Такой подход объясняется тем, что в неоклассических произв. функциях технический прогресс задаётся экзогенно. Впервые широкое применение неоклассическая п. ф. получила своё развитие в работах Соллоу. П.ф. Y=F(K,L) называется неоклассич., если она является гладкой (дифференцируемой в любой точке области, не имеет разрывов) и удовлетворяет следующим условиям, поддающимся естественной экономической интерпретации:
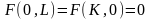 -
при отсутствии одного из ресурсов
производство невозможно;
-
при отсутствии одного из ресурсов
производство невозможно;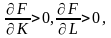 -
с ростом ресурсов выпуск растет;
-
с ростом ресурсов выпуск растет;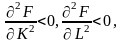 -
с увеличением ресурсов скорость роста
выпуска замедляется;
-
с увеличением ресурсов скорость роста
выпуска замедляется;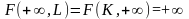 -
при неограниченном увеличении одного
из ресурсов выпуск неограниченно
растет;
-
при неограниченном увеличении одного
из ресурсов выпуск неограниченно
растет;
В своей работе,
посвящённой проблеме построения модели
экономического роста Соллоу использовал
линейно однородную неоклассическую
производственную ф-ю Y=F(K,L),
обладающую стандартным набором свойств
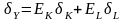 ,
где
,
где
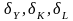 темпы
изменения выпуска, темпы изменения
капитала и труда соответственно.
темпы
изменения выпуска, темпы изменения
капитала и труда соответственно.
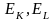 -
эластичности выпуска по капиталу и
труду. Частным случаем НПФ является ф-я
Кобба-Дугласа
-
эластичности выпуска по капиталу и
труду. Частным случаем НПФ является ф-я
Кобба-Дугласа
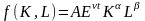 ,
где
,
где
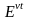 -
показатель технического прогресса, A
– коэфф-т шкалы, некий свободный член
при логарифмировании. α,β>0 – показатели
эластичности выпуска по капиталу и
труду, они показывают на какую величину
изменится Y
если α или β увеличить на 1%.Если α+β=1, то
уровень эффективности не зависит от
масштабов производства. Если α+β<1, то
средние издержки рассчитанные на единицу
продукции, растут, а при α+β>1 средние
издержки убывают по мере расширения
масштабов производства. Эластичность
выпуска
продукции по капиталу и труду равна
соответственно
и ,
так как
и
-
показатель технического прогресса, A
– коэфф-т шкалы, некий свободный член
при логарифмировании. α,β>0 – показатели
эластичности выпуска по капиталу и
труду, они показывают на какую величину
изменится Y
если α или β увеличить на 1%.Если α+β=1, то
уровень эффективности не зависит от
масштабов производства. Если α+β<1, то
средние издержки рассчитанные на единицу
продукции, растут, а при α+β>1 средние
издержки убывают по мере расширения
масштабов производства. Эластичность
выпуска
продукции по капиталу и труду равна
соответственно
и ,
так как
и
Производительность труда показывает степень результативности использования трудовых ресурсов и вычисляется по формуле x=Y/L Фондоотдача (капиталоотдача) характеризует уровень плодотворности применения основного капитала (основных фондов) и вычисляется по формуле z=Y/K Предельная производительность труда и капитала Для расчета этих величин определим частные производные функции по каждому из факторов: (dY/dК)= r – предельная производительность капитала (фондоотдача), (dY/dL)= w – предельная производительность труда. Таким образом, увеличение затрат капитала на 1 единицу при неизменных объемах используемого труда приведет к росту выпуска продукции на r единиц, а увеличение затрат труда на 1 единицу при неизменных объемах капитала приведет к росту выпуска на w единиц.
Для мультипликативной функции вытекает, что предельная фондоотдача пропорциональна средней фондоотдаче (Y/K) c коэффициентом , а предельная производительность труда – средней производительности труда (Y/L) с коэффициентом : Предельная норма замещения труда капиталом Эта величина обозначается S и равняется (dY/dL) делить на (dY/dК). Таким образом, если затраты труда уменьшатся на 1 единицу, то при неизменном выпуске продукции затраты капитала увеличатся на S единиц.
