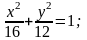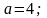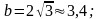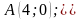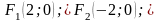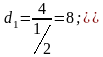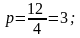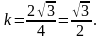МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
РАСЧЁТНО - ГРАФИЧЕСКОЙ РАБОТЫ «КРИВЫЕ ВТОРОГО ПОРЯДКА»
Для выполнения расчётно-графической работы необходимо:
Для центрированных кривых.
Выписать уравнение кривой второго порядка (выдаётся преподавателем);
Определить и написать тип кривой второго порядка.
Привести уравнение кривой к каноническому виду;
Выписать параметры a, b.
Определить ось, на которой будут расположены фокусы.
Выписать координаты вершин.
Вычислить и выписать фокусное расстояние, эксцентриситет, фокальный параметр и
коэффициент сжатия.
Выписать координаты фокусов.
Написать уравнения директрис.
Изобразить полученную линию второго порядка, а также фокусы и
директрисы (для гиперболы – и асимптоты).
Оформление расчётно-графической работы:
Титульный лист должен содержать:
наименование выполняемой работы,
вариант,
номер группы,
фамилию и.о. студента,
дату выполнения работы.
Работа выполняется двойных листках в клетку.
График чертится карандашом, аккуратно.
Должны быть подписаны оси, указан масштаб (выбирается самостоятельно), отмечены вершины, фокусы.
Директрисы и асимптоты гиперболы - начерчены другим цветом и рядом написаны их уравнения.
Кривые второго порядка.
Определение
1:
Линией
(кривой) второго порядка называется
множество точек плоскости, декартовы
координаты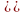 которых удовлетворяют алгебраическому
уравнению второй степени:
которых удовлетворяют алгебраическому
уравнению второй степени:
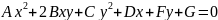 (
1 )
(
1 )
где
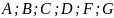 - постоянные действительные числа.
- постоянные действительные числа.
Уравнение (1) называется общим уравнением кривой второго порядка.
Мы
будем рассматривать уравнения, в которых
коэффициент
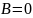 .
.
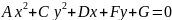 (
2 )
(
2 )
Если не существует точек с действительными координатами, удовлетворяющми уравнению (1), то говорят, что уравнение ( 1 ) определяет мнимую кривую второго порядка.
Уравнение x2 + y2 = −1 может служить примером уравнения второй степени, определяющего мнимую кривую, в данном случае мнимую окружность.
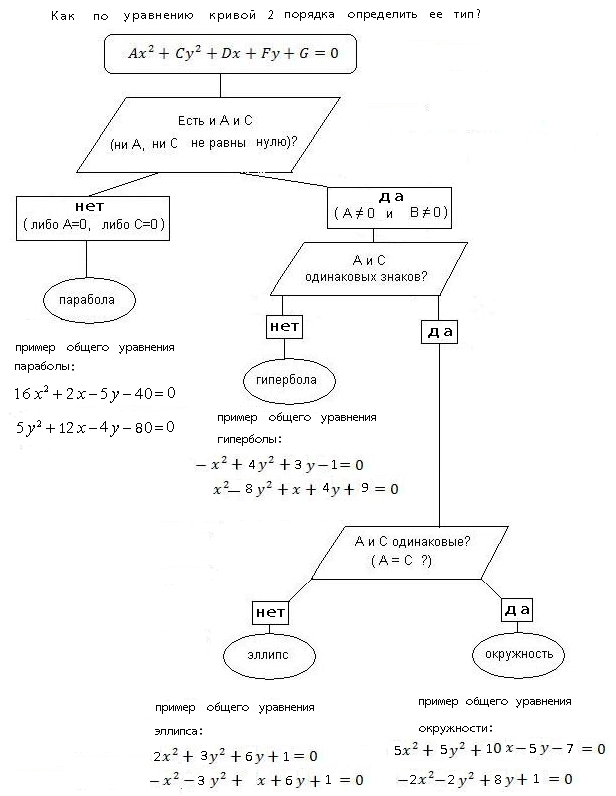
НАПРИМЕР:
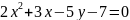
В уравнении присутствует только одна переменная во 2-й степени. Следовательно это уравнение параболы.
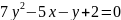
В этом уравнении - тоже только одна переменная во 2-й степени. Следовательно это тоже уравнение параболы.
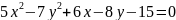 .
.
В этом уравнении присутствуют обе переменные во 2-й степени (это уравнение
не является уравнением параболы).
Сравним знаки перед
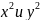 .
Знаки различные, следовательно это
уравнение
.
Знаки различные, следовательно это
уравнение
гиперболы.
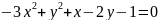 .
.
В данном уравнении - обе переменные во 2-й степени (это уравнение не является уравнением параболы).
Сравним знаки перед . Они различные, значит это уравнение тоже
описывает гиперболу.
 .
.
В этом уравнении присутствуют обе переменные во 2-й степени (следовательно уравнение не является уравнением параболы).
Сравним знаки перед . Знаки одинаковые (это уравнение не является уравнением гиперболы).
Сравним коэффициенты перед .Они различные, следовательно это уравнение эллипса.

Обе переменные - во 2-й степени (следовательно это не парабола).
Сравним знаки перед . Они одинаковые (следовательно это не гипербола).
Сравним коэффициенты перед . Они различные, значит это тоже эллипс.
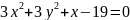 .
.
Здесь обе переменные во 2-й степени (следовательно это не парабола).
Сравним знаки перед . Они одинаковые (следовательно это не гипербола).
Сравним коэффициенты перед . Они тоже одинаковые, следовательно это уравнение описывает окружность.
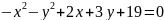 .
.
Здесь обе переменные во 2-й степени (следовательно это не парабола) .
Сравним знаки перед . Они одинаковые (следовательно это не гипербола).
Сравним коэффициенты перед . Они тоже одинаковые, значит это окружность.
x2 + y2 – 4x + 6y – 12 = 0
4x2 + 4y2 + 2x -16 = 0
- x2 - y2 + 4x + 2y -6 = 0
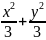
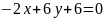
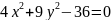
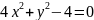
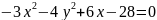

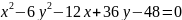


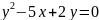
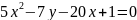

Ответы: 1-4 – окружность; 5-8 – эллипс; 9;10 – гипербола; 11 – 14 – парабола.
Э ллипс.
Определение.
Эллипсом
называется множество точек плоскости,
декартовы координаты которых удовлетворяют
уравнению
 ,
где
,
где
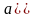 .
.
Это уравнение является каноническим уравнением эллипса.
Построение эллипса.
Р ассмотрим
случай, когда
ассмотрим
случай, когда
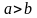 .
.
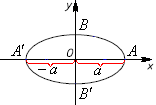
От
начала координат вправо и влево по оси
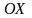 отложим величину, равную
отложим величину, равную
 .
Полученные точки обозначим буквами
.
Полученные точки обозначим буквами
 и
и
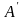 .
.
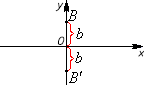
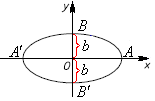
Вверх
и вниз от начала координат вдоль оси
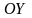 отложим величину, равную
отложим величину, равную
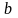 .
Полученные точки обозначим буквами
.
Полученные точки обозначим буквами
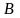 и
и
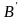 .
.
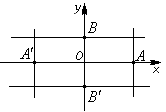
Через
точки
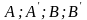 проведем
прямые, параллельные осям координат.
проведем
прямые, параллельные осям координат.
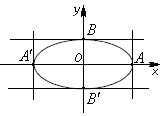
В
полученный прямоугольник впишем эллипс.
Точки
- называются вершинами эллипса. Они
имеют координаты: ;
;
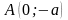 ;
;
 ;
;
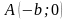 .
Отрезки между вершинами называются
большой и малой осями эллипса. Отрезки
между началом координат и вершинами
называются большой и малой полуосями
эллипса. В данном случае
.
Отрезки между вершинами называются
большой и малой осями эллипса. Отрезки
между началом координат и вершинами
называются большой и малой полуосями
эллипса. В данном случае
 большой
осью эллипса называется отрезок
большой
осью эллипса называется отрезок
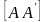 ,
а
малой осью -
,
а
малой осью -
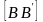 .
Большой полуосью эллипса называется
отрезок
.
Большой полуосью эллипса называется
отрезок
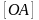 ,
а
малой полносью -
,
а
малой полносью -
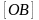 .
.
Ф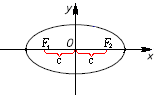 окусами
эллипса
называются точки
окусами
эллипса
называются точки
 и
и
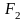 ,
расположенные на большой оси на
одинаковом расстоянии от начала
координат. Координаты фокусов:
и
,
где
,
расположенные на большой оси на
одинаковом расстоянии от начала
координат. Координаты фокусов:
и
,
где
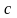 -
расстояние от начала координат до
каждого из фокусов:
-
расстояние от начала координат до
каждого из фокусов:
 .
.
Величины
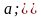 связаны равенством:
связаны равенством:
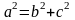 или
или
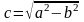 .
Фокусное расстояние (расстояние между
фокусами)
.
Фокусное расстояние (расстояние между
фокусами)
 .
.
Эксцентриситет.
Эксцентриситет
эллипса равен отношению фокусного
расстояния к длине большой оси:
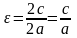 .
Так как у эллипса
.
Так как у эллипса
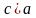 ,
то эксцентриситет эллипса меньше
единицы
,
то эксцентриситет эллипса меньше
единицы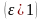 .
.
Эксцентриситет
эллипса показывает степень «вытянутости»
эллипса. Чем больше эксцентриситет,
тем больше вытянут эллипс. При очень
малом
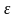 числа
числа
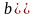 почти равны и эллипс напоминает
окружность. В предельном случае, когда
почти равны и эллипс напоминает
окружность. В предельном случае, когда
 ,
т. е. когда эллипс обращается в окружность,
его эксцентриситет обращается в 0.
,
т. е. когда эллипс обращается в окружность,
его эксцентриситет обращается в 0.
Ф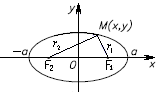 окальными
радиусы.
окальными
радиусы.
Возьмем
произвольную точку
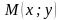 ,
принадлежащую эллипсу и проведем
отрезки, соединяющие эту точку с каждым
из фокусов:
,
принадлежащую эллипсу и проведем
отрезки, соединяющие эту точку с каждым
из фокусов:
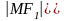 . Эти
отрезки называются фокальными радиусами
и обозначаются
. Эти
отрезки называются фокальными радиусами
и обозначаются
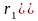 .
.
Свойство
1:
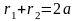 .
Это - характеристическое свойство
эллипса: сумма расстояний от любой
точки эллипса до фокусов – величина
постоянная и равна длине большой оси
.
Это - характеристическое свойство
эллипса: сумма расстояний от любой
точки эллипса до фокусов – величина
постоянная и равна длине большой оси
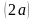 .
.
Длины
фокальных радиусов:
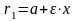
 .
.
Директрисы.
Д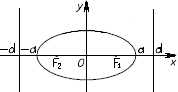 иректрисы
– 2 прямые, перпендикулярные большой
оси и симметричные относительно начала
координат. Директрисы обозначаются
иректрисы
– 2 прямые, перпендикулярные большой
оси и симметричные относительно начала
координат. Директрисы обозначаются
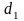 и
и
 .
Уравнения директрис:
.
Уравнения директрис:
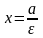
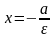 .
Директрису
и фокус, лежащие по одну сторону от
центра, будем называть соответствующими
друг другу.
.
Директрису
и фокус, лежащие по одну сторону от
центра, будем называть соответствующими
друг другу.
С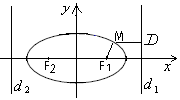 войство
2:
войство
2:
Возьмем на линии произвольную точку
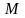 и
проведем
и
проведем
из нее 2 отрезка:
-
до фокуса
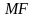 (фокальный радиус)
(фокальный радиус)
-
до директрисы
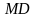 .
.
Найдем длины этих отрезков.
Эксцентриситет равен отношению расстояния от точки М до фокуса к расстоянию от точки М до соответствующей директрисы:
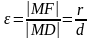 .
.
Эксцентриситет
есть величина постоянная. Для эллипса
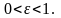 .
.
Ф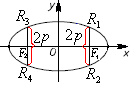 окальная
хорда.
окальная
хорда.
Через
точки, в которых расположены фокусы
эллипса проведем прямые, перпендикулярные
большой оси. Точки пересечения эллипса
с этими прямыми обозначим буквами
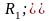 Получившиеся отрезки
Получившиеся отрезки
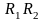 и
и
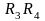 называются
фокальными хордами и обозначаются
называются
фокальными хордами и обозначаются
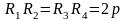 ,
где
,
где
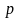 - фокальный параметр.
- фокальный параметр.
Ф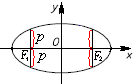 окальный
параметр.
окальный
параметр.
Фокальным
параметром
называется половина длины фокальной
хорды. Он вычисляется по формуле:
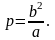
Коэффициент сжатия.
О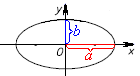 тношение
длин малой и большой полуосей
тношение
длин малой и большой полуосей
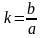 называется
коэффициентом
сжатия
эллипса или эллиптичностью. Коэффициент
сжатия и эксцентриситет эллипса связяны
между собой соотношением:
называется
коэффициентом
сжатия
эллипса или эллиптичностью. Коэффициент
сжатия и эксцентриситет эллипса связяны
между собой соотношением:
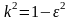 .
Для окружности коэффициент сжатия
равен единице, сжатие — нулю.
.
Для окружности коэффициент сжатия
равен единице, сжатие — нулю.
Сжатие.
Величина,
равная
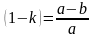 называется сжатием
эллипса.
называется сжатием
эллипса.
Радиус эллипса.
Радиус
эллипса в данной точке (расстояние от
его центра до данной точки) вычисляется
по формуле
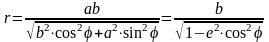 ,
где
,
где
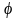 —
угол между радиус-вектором
данной точки и осью
абсцисс.
—
угол между радиус-вектором
данной точки и осью
абсцисс.
Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
Если для точки
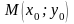 выполняется условие
выполняется условие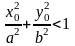 ,
то она находится вгутри эллипса. Если
выпонено
,
то она находится вгутри эллипса. Если
выпонено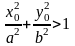 ,
то снаружи.
,
то снаружи.
Для эллипса оси координат являются осями симметрии, а начало координат – центром симметрии.
Пользуясь определением эллипса, его легко построить непрерывным движением карандаша. Для этого берём нерастяжимую нить длиной, равной большой оси эллипса, т.е. длиной 2а, и закрепляем концы этой нити в фокусах, положение которых предполагается известным. Натягиваем нить карандашом и остриём его описываем кривую, держа нить всё время в натянутом состоянии. Кривая, описываемая при этом – эллипс, так как сумма расстояний от любой точки этой кривой до фокусов равна длине нити, т.е. равна постоянной величине.
Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
Если
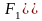 — фокусы эллипса, то для любой точки
— фокусы эллипса, то для любой точки
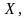 принадлежащей эллипсу, угол между
касательной в этой точке и прямой
принадлежащей эллипсу, угол между
касательной в этой точке и прямой
 равен углу между этой касательной и
прямой
равен углу между этой касательной и
прямой
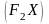 .
.
Оптические свойства:
Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
Свет от источника, находящегося вне любого фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
Данное свойство имеет достаточно простой физический смысл. Если из одного фокуса выходит в плоскости эллипса луч света, то отразившись от самого эллипса, он обязательно пройдет через другой фокус. Возьмем поверхность, образованную вращением эллипса вокруг большой оси, и будем считать, что внутри она зеркальная. В один из фокусов поместим источник света. Тогда все лучи, выходящие из источника, отражаясь от поверхности, пройдут через другой фокус, то есть освещенность в обоих фокусах будет одинаковой.
Эллипс
- фигура, состоящую из всех тех точек
плоскости, сумма расстояний от которых
до двух заданных точек
и
(называемых фокусами эллипса)
является постоянной величиной, обычно
обозначаемой через
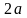 .
.
З
 ная
определение эллипса, можно сделать
простейший прибор, вычерчивающий
эллипс. Для этого надо связать две
булавки ниткой и воткнуть их в чертежную
доску (рис. 2), взять карандаш и двигать
его по бумаге так, чтобы грифель карандаша
все время натягивал нитку. Тогда кончик
грифеля будет рисовать на бумаге эллипс.
ная
определение эллипса, можно сделать
простейший прибор, вычерчивающий
эллипс. Для этого надо связать две
булавки ниткой и воткнуть их в чертежную
доску (рис. 2), взять карандаш и двигать
его по бумаге так, чтобы грифель карандаша
все время натягивал нитку. Тогда кончик
грифеля будет рисовать на бумаге эллипс.
Этот способ с успехом используют, садовники при изготовлении цветочных эллиптических клумб. Вместо кнопок в землю втыкают два кола, кольцо делается из толстой веревки, а эллипс вычерчивается на земле не карандашом, а палкой .
Оптическое свойство эллипса лежит в основе интересного акустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Лабораторная работа. Укажем способ получения эллипса из листа бумаги. Вырежем из бумаги большой круг и в любом его месте, отличном от центра, поставим точку F. Сложим круг так, чтобы эта точка совместилась с какой-нибудь точкой F’ окружности круга, и на бумаге образовалась линия сгиба a . Линия сгиба будет серединным перпендикуляром к отрезку FF’ и, следовательно, касательной к эллипсу. Разогнем круг и снова согнем его, совместив точку с другой точкой окружности круга. Сделаем так несколько раз, пока вся бумага не покроется линиями сгибов. Линии сгибов будут касательными к эллипсу. Граница участка внутри этих сгибов будет иметь форму эллипса.
Р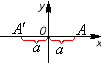 ассмотрим
случай, когда
ассмотрим
случай, когда
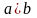 .
.
От начала координат вправо и влево по оси отложим величину, равную . Полученные точки обозначим буквами и .
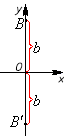
Вверх и вниз от начала координат вдоль оси отложим величину, равную . Полученные точки обозначим буквами и .
Через полученные точки проведем прямые, параллельные осям координат.
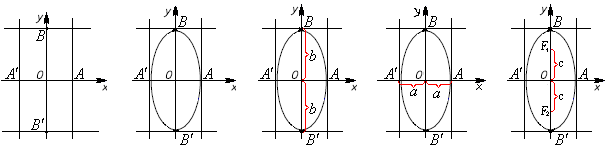
В полученный прямоугольник впишем эллипс. Точки - называются вершинами эллипса. Они имеют координаты: ; ; ; .
Большой осью эллипса называется отрезок , а малой осью - . Большой полуосью эллипса называется отрезок , а малой полносью - .
Фокусами
эллипса имеют координатами
и
,
где
:
.
Величины
связаны
равенством:
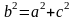
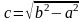 .
.
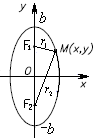
Характеристическое
свойство эллипса:
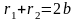 .
.
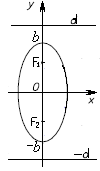
Эксцентриситет
эллипса равен отношению фокусного
расстояния к длине большой оси:
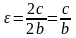 .
Так как у эллипса
.
Так как у эллипса
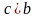 ,
то эксцентриситет эллипса меньше
единицы.
,
то эксцентриситет эллипса меньше
единицы.
Уравнения
директрис:
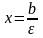
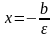 .
.
Пример
1:
Дан эллипс
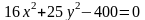
Написать каноническое уравнение эллипса, определить длину его осей, выписать координаты его вершин и фокусов, эксцентриситет, начертить эллипс, директрисы эллипса и написать их уравнения.
Решение:
Приведем
уравнение эллипса к каноническому
виду:

Перенесем свободный член в правую часть равенства
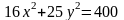 и
разделим на него левую и правую части
равенства
и
разделим на него левую и правую части
равенства
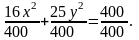
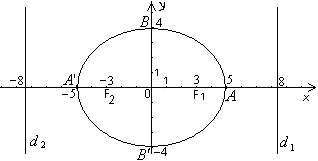 После
сокращения получим каноническое
уравнение эллипса:
После
сокращения получим каноническое
уравнение эллипса:
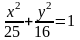 или
или
 .
.
Находим
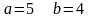 .
.
.
.
длина
большой оси:
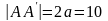 .
Длина
малой оси:
.
Длина
малой оси:
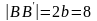 .
.
Координаты вершин:
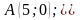 .
.
.
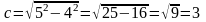 .
.
Координаты
фокусов:
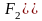
Эксцентриситет
вычислим по формуле:

Фокальный
параметр:
вычисляется по формуле:
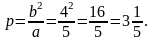
Коэффициент
сжатия:
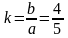
Уравнения
директрис:

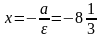 .
.
П ример
2:
Дан эллипс
ример
2:
Дан эллипс
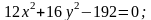
Написать каноническое уравнение эллипса,
определить длину его осей, выписать координаты его вершин и фокусов, эксцентриситет, фокальный параметр, начертить эллипс, директрисы эллипса и написать их уравнения.
Решение: