МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»

ЕН.Ф.01 МАТЕМАТИКА

Методические указания и задания к выполнению расчетно-графической работы № 2 для студентов всех специальностей

Уфа 2010

00УДК 51(07)

ББК 22.1я73,22.161.6

М 54

Рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства протокол № ________ от ________________ 2010 г.

Составитель: доцент Дик Е.Н.

Рецензент: доцент кафедры физики Юмагужин Р.Ю.

Ответственный за выпуск: зав. кафедрой математики доцент

Лукманов Р.Л.

Введение

Методические указания представили классическую форму самостоятельной деятельности в виде вариантов расчетно-графической работы, позволяющих осуществить индивидуальную проверку знаний студентов, а также способствующих приобретению ими устойчивых навыков в решении задач по указанной теме. Рассмотрены разделы векторной алгебры и аналитической геометрии на плоскости и в пространстве. В частности, выбраны задания по темам: скалярное, векторное и смешанное произведение векторов; определение уравнений линий первого и второго порядка; взаимное расположение прямой и плоскости; нахождение элементов пространственной фигуры. В настоящем сборнике представлены тридцать индивидуальных вариантов, каждый из которых содержит шесть заданий и примеры решения типовых задач. Варианты заданий выдаются преподавателем. Приводится библиографический список, рекомендуемый для дополнительного изучения, имеющийся в наличии в библиотеке БГАУ.

Представляем решение некоторых типовых заданий.

Задача 1. Найти косинус угла между векторами и .

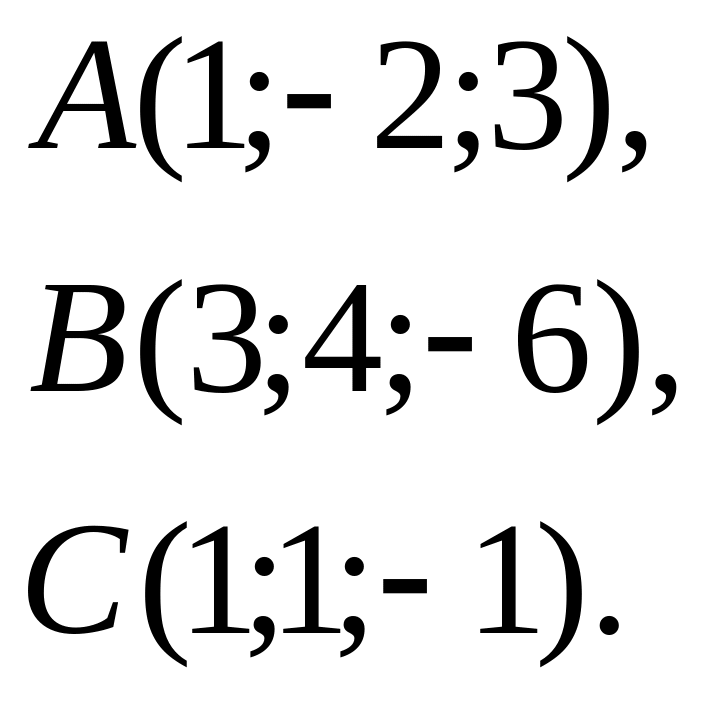
Решение.

Задача 2. Показать, что x² + y² + 4x - 6y - 3 = 0 есть уравнение окружности. Найти ее центр и радиус.

Решение.

Заданное уравнение преобразуем к виду (x - a)² + (y - b)² = r².   (1)

Выпишем члены, содержащие только x, и члены, содержащие только y. Выделим полные квадраты каждой переменной:

x² + 4x = (x + 2)² - 4,

y² - 6y = (y - 3)² - 9.

Левая часть уравнения запишется теперь так:

или отсюда

(x + 2)² + (y - 3)² = 16.   (2)

Сравнивая уравнение (2) с (1), заключаем, что уравнение определяет окружность, центр которой имеет координаты О(-2, 3), r² = 16, а r = 4.

Задача 3. Дана равносторонняя гипербола x² - y² = 8. Найти уравнение эллипса, фокусы которого находятся в фокусах гиперболы, если известно, что эллипс проходит через точку A(4, 6).

Решение.

Уравнение гиперболы преобразуем к каноническому виду и получим , . Из соотношения получаем, что c = 4. Значит, координаты фокусов гиперболы F₂(-4, 0) и F₁(4, 0). В этих точках находятся фокусы эллипса. Обозначим большую и малую полуоси эллипса через a₁ и b₁. Расстояние между фокусами эллипса такое же, как и расстояние между фокусами гиперболы. Поэтому половину этого расстояния по-прежнему обозначим через c. Но у эллипса

т. е. и (1)

Для определения a₁ и b₁ нужно найти еще одно соотношение, связывающее их. Искомое уравнение эллипса запишется так:

    (2)

Поскольку точка A(4, 6) лежит на эллипсе, ее координаты должны удовлетворять уравнению эллипса. Подставляя в последнее уравнение x = 4, y = 6, получаем, что . Присоединяя уравнение (1) к этому уравнению, получаем для определения и систему уравнений:

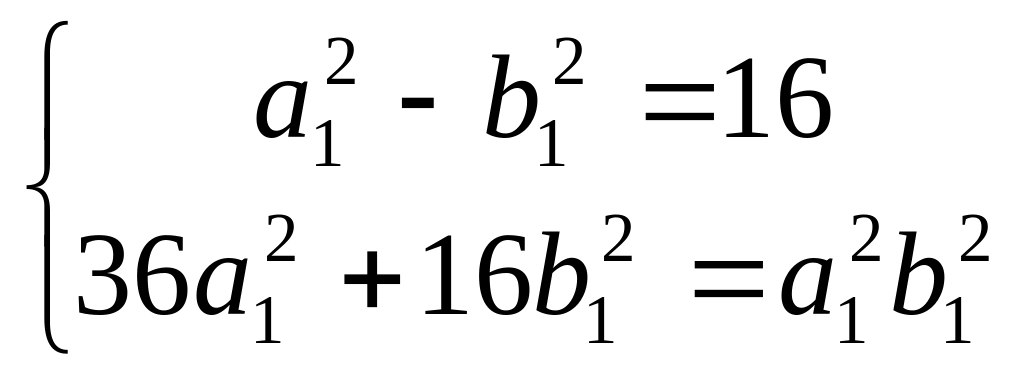
Откуда ; . Подставляя эти значения в (2), находим искомое уравнение .

Задача 4. Вычислить площадь параллелограмма, построенного на векторах и .

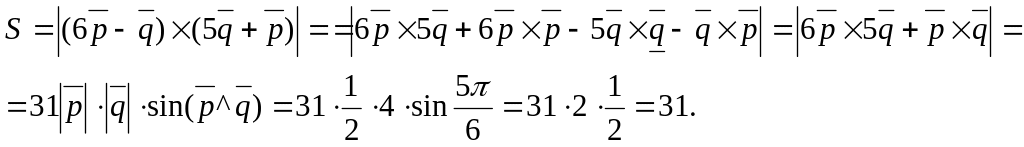
Задача 5. Вычислить объем тетраэдра с вершинами в точках и его высоту, опущенную из вершины на грань .

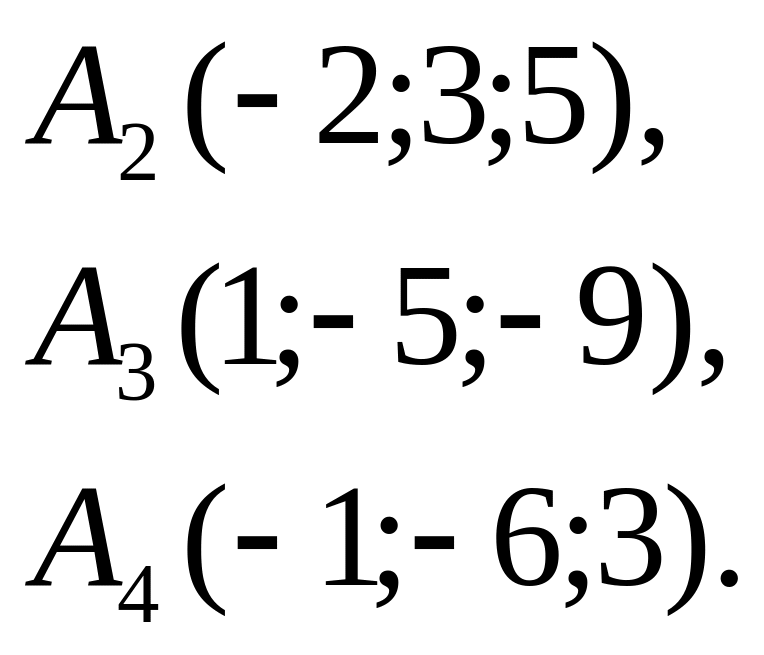
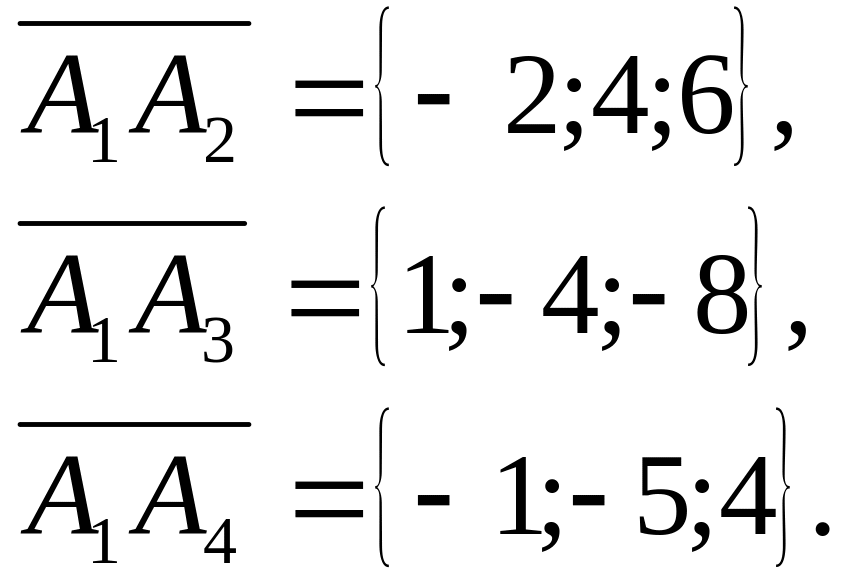
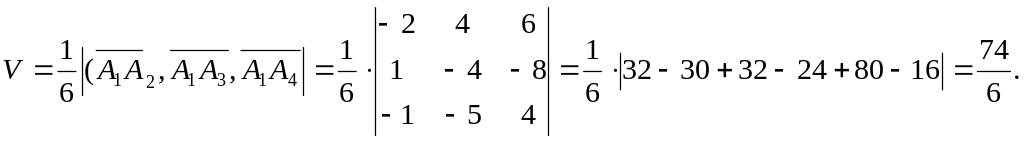
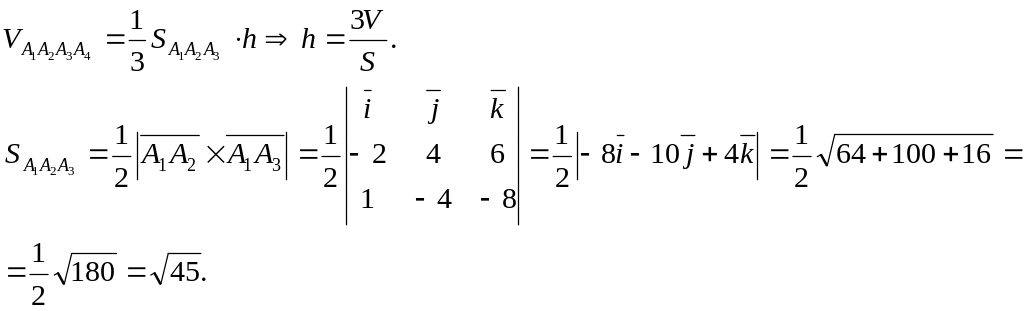
Задача 6. Найти расстояние от точки до плоскости, проходящей через точки .

Уравнение плоскости, проходящей через 3 точки имеет вид:

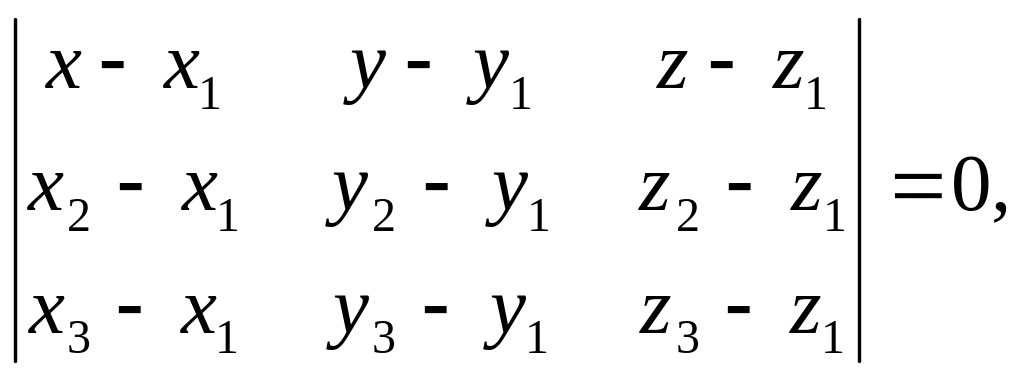
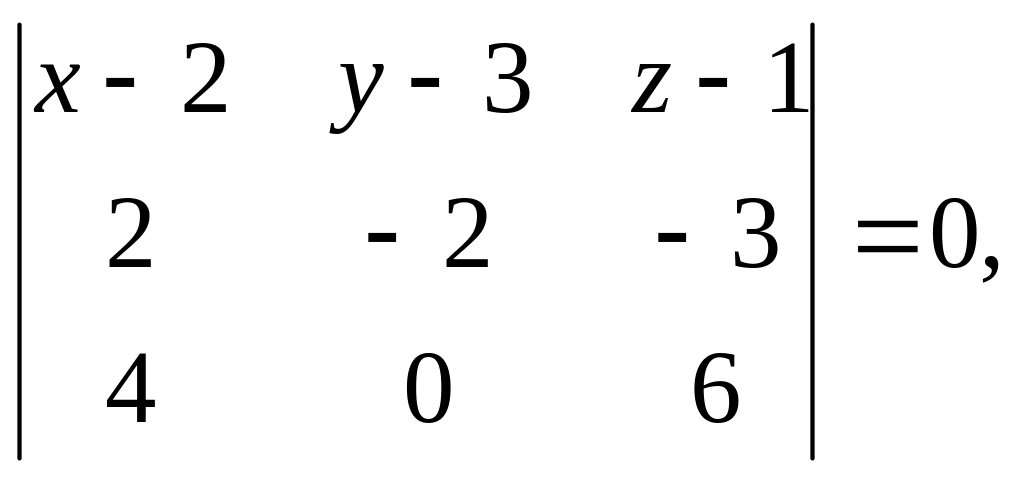
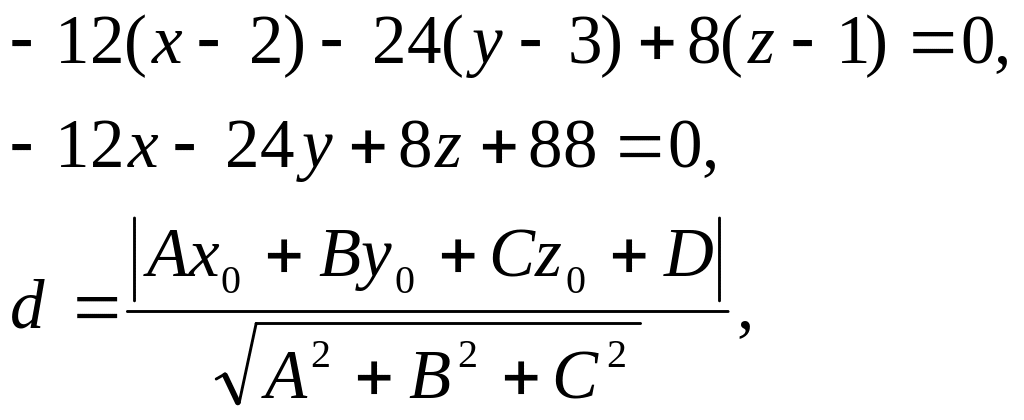
Задача 7. Найти точку , симметричную точке относительно прямой L, заданной уравнением

Поместим прямую в некоторую плоскость α и составим ее уравнение откуда . Найдем точку пересечения прямой L и плоскости α.

- координаты точки пересечения.

Отсюда,

Следовательно, - искомая точка.