18. Решение краевой задачи для уравнения колебания струны методом Фурье.

Решение уравнения будем искать в виде при граничных условиях: . Тогда X(0) = X(l) = 0.

Подставим решение в исходное уравнение:

Можно показать, что функции Х и Т имеют вид:

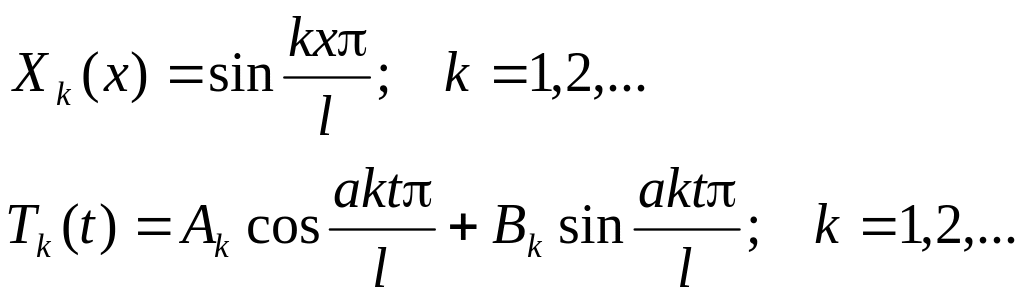
Все решения исходного дифференциального уравнения, удовлетворяющие граничным условиям, можно записать в виде:

Окончательно решение уравнения колебаний струны можно записать в виде:

где

19. Колебания бесконечной струны. Формула Даламбера.

В случае если длина струны очень велика, то на колебания, возникающие в середине струны, концы струны влияния практически не оказывают. Поэтому, рассматривая колебания бесконечной струны, уравнение , решается только при начальных условиях:

Для нахождения решения введем новые переменные: Тогда исходное уравнение принимает вид: Решением этого уравнения будет функция , где  и  - некоторые функции, которые будем считать дважды дифференцируемыми.

Получаем:

Если продифференцировать полученный ответ, получим:

Т.е. .

Далее с использованием начальных условий находим функции  и .

Проинтегрировав последнее равенство на отрезке [0, x], получаем:

Тогда:

Решение задачи Коши получаем в виде:

Эта формула называется формулой Даламбера.

20. Вывод уравнения теплопроводности в конечном стержне. Постановка первой краевой задачи.

Рассмотрим однородный цилиндрический стержень, боковая поверхность которого изолирована от внешнего пространства.

Направим Ох вдоль оси стержня и обозначим через и(х, t) температуру в сечении стержня с абсциссой х в момент t. Пусть АВ - элемент стержня, заключенный между сечениями х и (см. черт.).

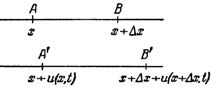
Будем считать промежуток времени столь малым, чтобы температуру в сечениях х и можно было принять неизменной (во времени). Опытом установлено, что количество тепла q, протекающее через какой-нибудь стержень, концы которого поддерживаются при постоянных температурах, пропорционально разности этих температур, площади сечения стержня, промежутку времени и обратно пропорционально длине стержня. Поэтому для элемента АВ можем написать:

(1)

где К—коэффициент пропорциональности, называемый коэффициентом внутренней теплопроводности, s — площадь поперечного сечения. В пределе при мы получим количество тепла Q, протекающее через сечение х, за время :

Рассмотрим опять элемент АВ. Количество тепла , которое получит этот элемент за время , выразится так:

(2)

(следует иметь в виду, что тепло течет в направлении, обратном тому, в котором возрастает температура). Величину можно подсчитать и другим способом.

Будем считать элемент АВ столь малым, что в каждый данный момент температуру всех его сечений можно считать одной и той же. Тогда

где с — теплоемкость вещества стержня, плотность (на единицу длины) и, следовательно, - масса элемента АВ. Сопоставление (1) и (2) дает:

и если перейти к пределу при и , то

(3)

где положено . Мы получили уравнение распространения тепла в стержне (или уравнение теплопроводности в линейном случае).

В зависимости от условий, в которых находятся концы стержня, можно поставить несколько задач.

Поставим задачу: найти функцию непрерывную для , имеющую непрерывные частные и для удовлетворяющую дифференциальному уравнению (3) для , и следующим условиям:

1) начальному условию , (4) где f(x) - заданная на отрезке непрерывная функция;

2) граничным условиям (5)

Таким образом, предполагается, что в начальный момент времени температура в стержне выражается функцией f(x), а на протяжении всего времени опыта на концах стержня искусственно поддерживается температура нуль.