5.6. Комбинаторный взрыв

Не так много алгоритмов имеют оценку сложности выше полиномиальной. Оценки сложности у большинства комбинаторных алгоритмов относятся ко второму классу.

Для них время решения Т как функция от размерности задачи T=f(n) имеет характер, показанный на рисунке. До какого-то критического значения n_кр время счета нарастает медленно, а затем следует резкий скачок.

Т

0 n_кр n

Такое явление называют комбинаторным взрывом. От него не спасает самый быстродействующий компьютер. Для каждой отдельной задачи значение n_кр может сдвигаться в ту или другую сторону.

Оно зависит от всех факторов, перечисленных в начале § 5.5. Но рано или поздно при увеличении размерности задачи время решения резко возрастет, и наступит явление комбинаторного взрыва.

Возможность комбинаторного взрыва – это основная опасность, которую следует учитывать при выборе метода решения комбинаторной задачи.

6. Полиномиальные алгоритмы

Полиномиальность алгоритма чаще всего связана с тем, что на дереве перебора выделено поддерево, для которого доказано, что оно содержит оптимальное решение. Доказательства полиномиальности алгоритмов в настоящем пособии не приводится. Их можно посмотреть в рекомендуемой литературе.

К одной из немногочисленных комбинаторных задач, имеющих полиномиальный алгоритм решения, относится задача построения минимального остовного дерева.

6.1. Построение минимального остовного дерева.

Дан взвешенный граф G(X, U, W), |X|=n, |U|=m, |W|=m.

Рассмотрим два алгоритма построения минимального остовного дерева.

6.1.1. Жадный алгоритм

1. Положить k=1.

2. Выбрать ребро с минимальным весом и включить его в дерево Т.

3. Если k<n-1, то перейти к п.4, иначе – к п.6.

4. Из оставшихся ребер выбрать ребро с минимальным весом и включить его в дерево Т, если оно не образует цикла с построенной частью.

5. Положить k=k+1. Перейти к п.3.

6. Конец алгоритма.

Пример. Рассмотрим на рис. 6.2а связный взвешенный граф G(X, U, W), |X|=n=6, |U|=m=9, |W|=m=9.

Процесс построения минимального остовного дерева при помощи жадного алгоритма изображен на рис. 6.2.

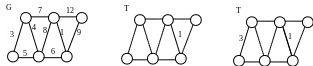
а) взвешенный граф б) выбор 1-го ребра в) выбор 2-го ребра

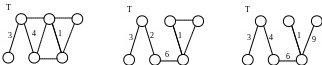
г) выбор 3-го ребра д) выбор 4-го ребра е) выбор 5-го ребра

Рис. 6.2. Построение минимального остовного

дерева жадным алгоритмом

Пунктиром обозначены ребра, среди которых на следующем шаге алгоритма ищется ребро с минимальным весом. Построенное дерево Т имеет суммарный вес ребер, равный 23.

При внимательном рассмотрении жадный алгоритм оставляет двойственное впечатление. С одной стороны он прост, но запрограммировать его – далеко не тривиальная задача. Дело в том, что в п.4 алгоритма содержится скрытый под алгоритм, заключающийся в определении возможного цикла в построенном дереве Т. Реализация же данного пол-алгоритма может сделать неэффективным сам жадный алгоритм.

Рассмотренный ниже алгоритм Прима свободен от этого недостатка. Он настолько прост, что трудно поверить в его корректность.