
- •Тема 8. Економетричні моделі динаміки
- •Практичне заняття № 2 (2 год.)
- •( Модуль 2 )
- •Приклади типових завдань.
- •1) Перевірити загальну якість даної моделі.
- •2) Перевірити значущість параметрів моделі .
- •3) Побудувати довірчі інтервали для параметрів моделі..
- •Нелінійні економетричні моделі
- •Тема: Фіктивні змінні в регресійних моделях
- •Тема: Мультиколінеарність факторів моделі
Тема 8. Економетричні моделі динаміки
Практичне заняття № 2 (2 год.)
( Модуль 2 )
Приклади типових завдань.
1. Розрахувати економетричну модель парної регресії між факторами Х і Y:
Ŷ = ǎ0 + ǎ1·х. Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0 , ǎ1.
Розрахувати за нею прогнозоване значення залежного фактора Y пр
Побудувати графік моделі парної регресії в кореляційному полі – “хмарі розсіювання”.
Розрахувати коефіцієнт детермінації R2 і коефіцієнт кореляції R. Який зміст цих коефіцієнтів ?
Оцінити якість отриманої моделі за F-, Т – критеріями із рівнем значущості α = 0,05.
.
у |
60 |
61 |
59 |
58 |
62 |
63 |
65 |
60 |
68 |
70 |
х |
30 |
35 |
33 |
34 |
36 |
38 |
40 |
41 |
45 |
45 |
Х – витрати на маркетинг, (тис. грн..), Y – прибуток , (млн. грн.).
2.
В результаті дослідження чинників
економічного зростання побудовано таку
модель (обсяг вибірки – 73 країни):
Y = 1,4 – 0,52X![]() + 0,17 X
+ 0,17 X![]() + 11,16 X
+ 11,16 X![]() – 0,38 X4
– 4,75 X
– 0,38 X4
– 4,75 X![]() + u,
+ u,
Т-кр.: (5,9) (4,34) (3,91) (0,79) (2,7) . R2 = 0,78.
де Y – темп росту середнього значення ВВП на душу населення у % до базового періоду;
X – реальні середні значення ВВП на душу населення, %; X – бюджетний дефіцит у % до ВВП;
X – обсяг інвестицій, % до ВВП; X4– зовнішній борг, % до ВВП; X – рівень інфляції, %.
1) Перевірити загальну якість даної моделі.
2) Перевірити значущість параметрів моделі .
3) Побудувати довірчі інтервали для параметрів моделі..
3. Побудовано модель залежності середньомісячної ринкової ціни акцій підприємства (Y, грн./акція) від обсягу сплачених дивідендів на акцію (Х1, грн./місяць) та обсягу коштів, спрямованих підприємством на розширення виробництва (Х2, сотні тис. грн. /міс.): yi = 2,4 + 1,6 хi1 + 0,9 хi2 + ui.
Відомо
також, що
![]() =
10,5,
=
10,5,
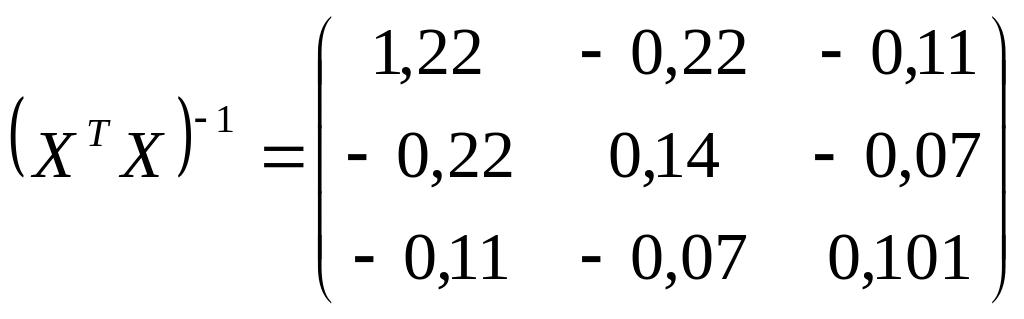 ,
n
= 20.
,
n
= 20.
Побудувати точковий та інтервальний прогнози для залежної змінної, якщо хпр.1 = 10, хпр.2 = 2.
-0,56043 |
1,905966 |
0,10066 |
0,178718 |
0,815776 |
0,297171 |
30,99719 |
7 |
2,737381 |
0,618174 |
5. Розрахована регресійна модель залежності прибутку (Y) від інвестицій (Х1), основного фонду виробництва (Х2), фонду робочого часу (Х3) за 20 спостереженнями:
0,140967 |
-0,41125 |
0,882323 |
-21,1336 |
0,076457 |
0,289052 |
0,215299 |
9,011057 |
0,973764 |
1,188204 |
# н/д |
# н/д |
148,4617 |
12 |
# н/д |
# н/д |
628,808 |
16,94196 |
# н/д |
# н/д |
