Внешняя задача Дирихле для шара.

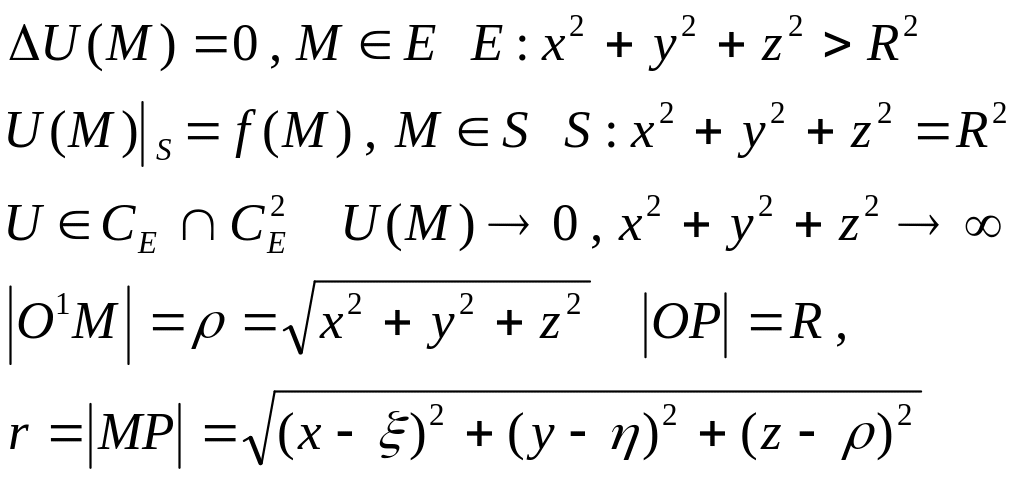
f(M) непрерывна на S ,

Решение внешней задачи Дирихле для

шара дается формулой 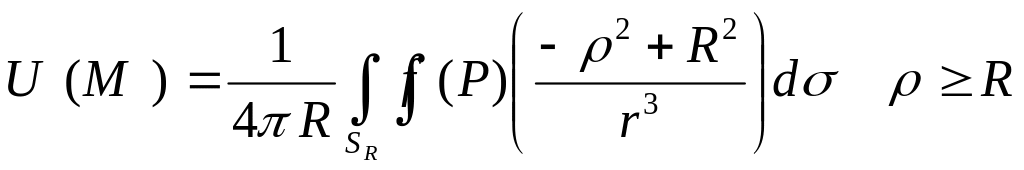(14)

Покажем что это так:

Покажем чтоU(M) из (14) гармоническая в E. Рассмотрим поведение U(M) на бесконечности. Пусть М настолько удалена от начала координат, что 2R

r-R  r/2. Тогда

покажем непрерывность примыкания к граничным условиям.

Для этого запишем (14) в сферических координатах

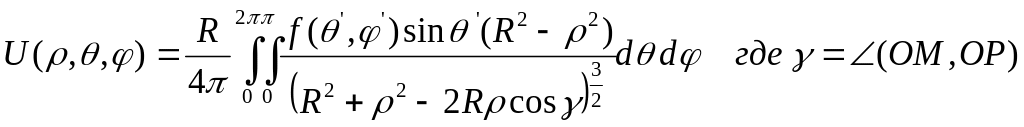
Выберем произвольно NS, покажем, что когда MN, U(M)f(N). Подвергнем точку М инверсии относительно поверхности сферы, т.е. найдем M₁(x₁,y₁,z₁) :

При М ,

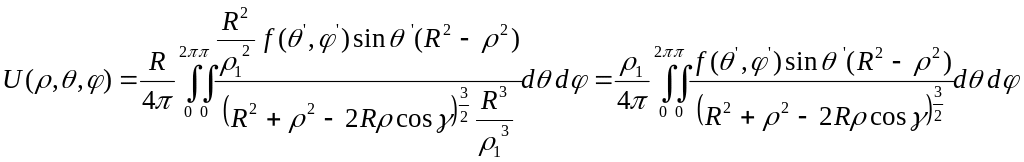
В силу R, как было показано ранее это выражение стремится к f(N). Т.о. (14) определяет решение внешней задачи Дирихле для шара.

Поведение производных функций, гармоничных на бесконечности. Пусть D- конечная область, D=S ,Е – внешняя по отношению к D бесконечная область.

Выберем в качестве начала координат некоторую внутреннюю точку области D и проведем из нее шар радиуса R так, что вся D лежала внутри шара.

Как было показано ранее U(M)<c/,

Подставим эту оценку

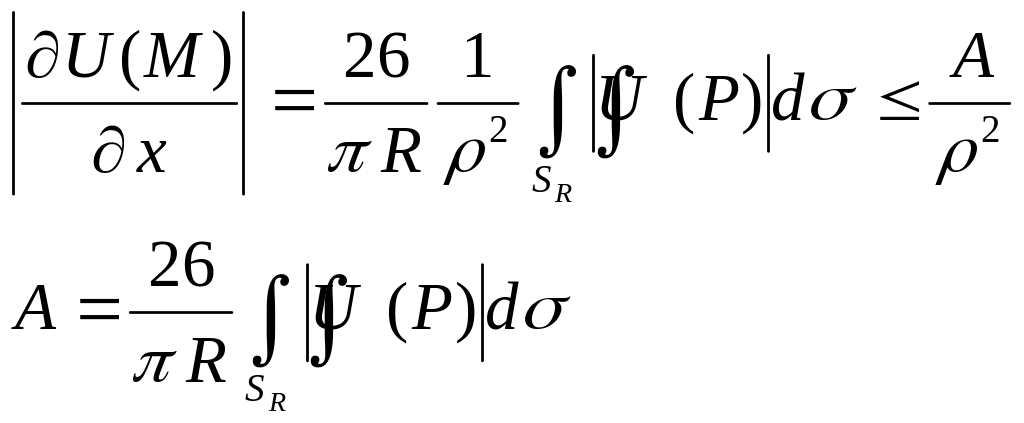
Аналогично т.к. А>C, то UA/ , 

Т.о. показали, что функции, ограниченные в областях, удовлетворяет заданному условию.

Решение задачи Неймана для шара.

Лемма. Если функция U(M) гармоничная в D, то и функция гармоническая в D.

Доказательство:

(*)

Соотношение (*) можно переписать в виде:

(1 )

Известно значение нормальной производной.

Теорема. Пусть V решение внутренней задачи Дирихле для шара, тогда (2’) является для шара внутренней задачей Неймана. Если V- решение внешней задачи Дирихле для шара, то (3’) решение внешней задачи Неймана.

Покажем, что U(M) в (2’) гармоническая.

=U()

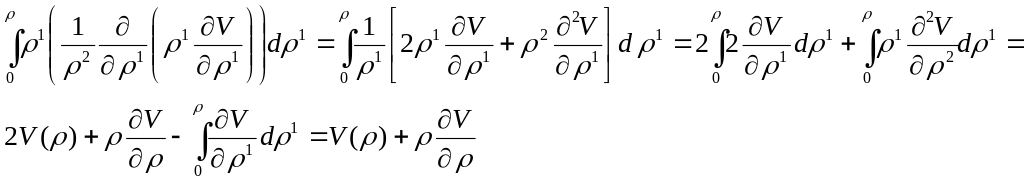
Аналогично можно показать что U(M) – гармоническая в(3’)

тогда из (1’) тогда для функции V по формуле Пуассона

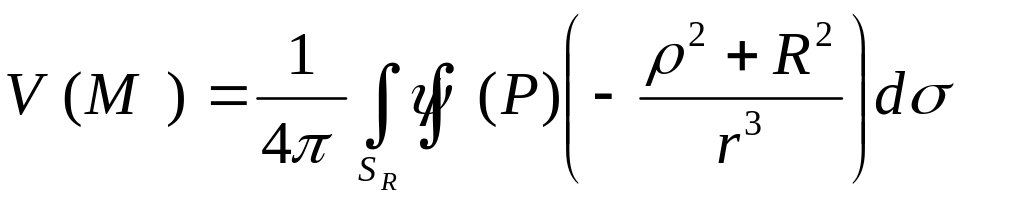
Для разрешимости задачи Неймана должно выполняться

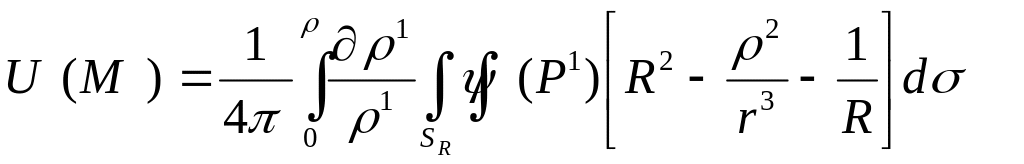
Меняя порядок интегрирования и проделывая преобразования можно получить (самостоятельно)

Аналогично для внешней задачи (самостоятельно)

Решение краевых задач для простейших областей методом Фурье.

Рассмотрим задачу Дирихле для круга

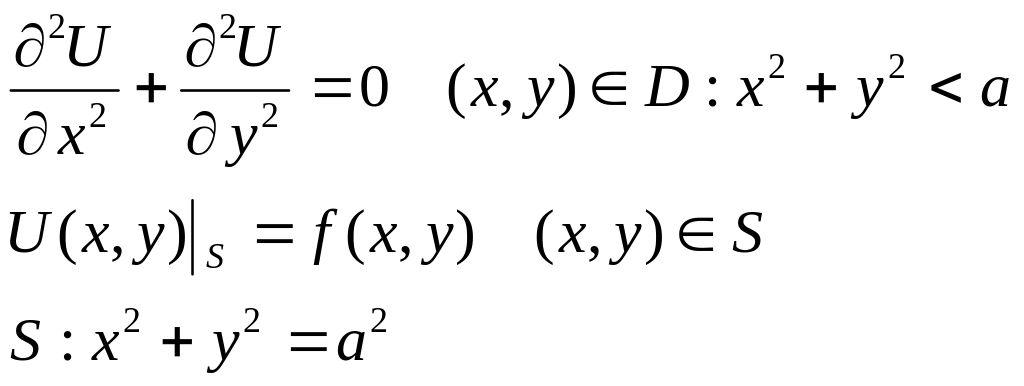
Перейдем к полярным координатам

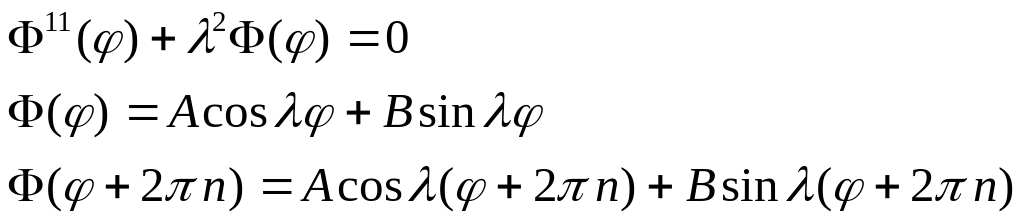
Очевидно периодичности по  можем добиться при  =k , k=0,1,2,…

введем t=ln

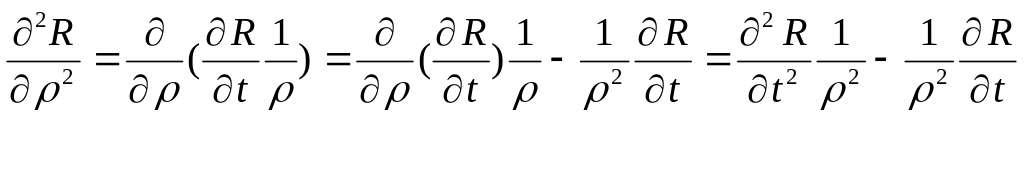
при к=0

при к=1,2,…

Из соображений ограниченности решений в О выберем

Найдем неизвестные константы из граничных условий

решение внутренней задачи Дирихле для круга. Аналогично можно показать, что для внешней задачи Дирихле для круга.

Теорема о среднем значении (Гаусса).

Значение гармонической функции в шаре равно среднему значению этой функции на поверхности.

Доказательство:

Пусть есть конечная D, U-гармоническая в D. Возьмем с центром в точке О шар радиуса R. U гармоническую в шаре описать до границы . Тогда для этой функции справедлива формула Грина (8). Рассматривая в качестве внутренней точки центр шара О
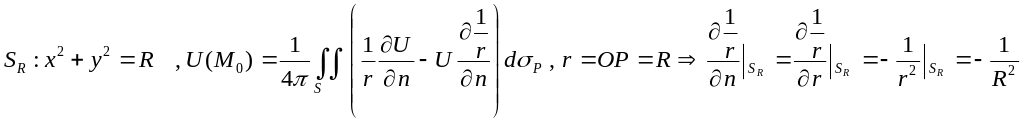