
- •Распространение тепла в пространстве.
- •Уравнения эллиптического типа.
- •Основные задачи для уравнения Лапласа и Пуассона.
- •Функция Грина задачи Дирихле.
- •Свойства функции Грина. Задачи Дирихле
- •Функция Грина задачи Неймана.
- •Построение функции Грина.
- •Следствие из формулы Пуассона.
- •Внешняя задача Дирихле для шара.
- •Решение задачи Неймана для шара.
- •Решение краевых задач для простейших областей методом Фурье.
- •Теорема о среднем значении (Гаусса).
- •Теория потенциалов. Несобственные интегралы зависящие от параметра.
- •Потенциал объема и его свойства.
Следствие из формулы Пуассона.
Рассмотрим конечную область D (достаточно гладкая поверхность S) и некоторое U(M): U(M)-0 , MD , U(M)>0.
Выберем произвольно
D.
Проведем через точку![]() ,
как через начало координат, шар радиуса
R,
чтобы он целиком лежал в D.Выберем
произвольно M
внутри шара.
,
как через начало координат, шар радиуса
R,
чтобы он целиком лежал в D.Выберем
произвольно M
внутри шара.
![]()
Справедлива формула Пуассона (11)
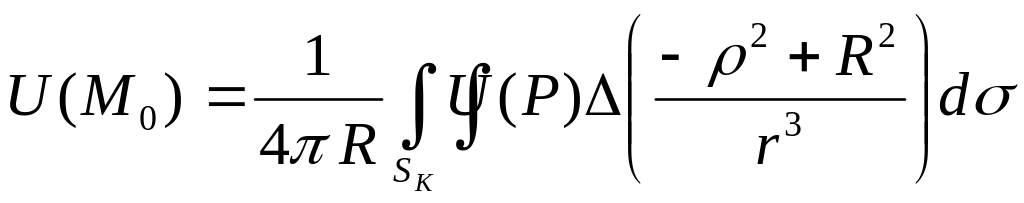
rR- , rR+ , тогда для ядра Пуассона справедлива оценка
![]()
![]()

![]()
Применяя с правой и левой части теорему о среднем, получим оценку :
Для гармонических положительных функций
![]() (12) -
оценка значений функции внутри шара
через значение в центре шара. Это
неравенство
Горнака.
(12) -
оценка значений функции внутри шара
через значение в центре шара. Это
неравенство
Горнака.
Теорема. Функция, гармоническая во всем промежутке равна 0.
Доказательство. Пусть U(M) - гармоническая функция во всем пространстве.
![]()
Опишем из начала координат сферу радиуса R. Если U – гармоническая функция внутри сферы, то по формуле (11) :
![]()
Выберем радиус
сферы настолько большим, чтобы
![]() , тогда
, тогда
![]()
В силу произвольности U(M)=0, а в силу произвольности выбора точки М
U(M) 0.
Теорема Лиувилля. Функция, гармоническая в любой конечной области и ограниченная при этом сверху или снизу, является постоянной.
Доказательство.
![]() .
То есть нам все равно, рассматривать
сверху или снизу. Будем считать
.
То есть нам все равно, рассматривать
сверху или снизу. Будем считать
![]() .
Не нарушая общности
.
Не нарушая общности
будем считать, что
![]() .
.
Проведем из центра координат сферу радиуса R. U(M) будет гармонической внутри шара, причем она внутри этого шара неотрицательная. Тогда можно оценить значение этого шара, воспользовавшись неравенством Гарнака:
![]()
Взяв достаточно
большое R,
получаем
![]()
Так как М – произвольная точка, то U const.
Теоремы о последовательностях гармонической функции.
Теорема 1.
Если последовательность
![]() непрерывных в замкнутой конечной области
и гармонических
непрерывных в замкнутой конечной области
и гармонических
![]() ,сходящихся равномерно на границе
области D
(D=S),
то она сходится равномерно во всех
внутренних точках области, причем
представляемая функция является
гармоничной внутри D.
,сходящихся равномерно на границе
области D
(D=S),
то она сходится равномерно во всех
внутренних точках области, причем
представляемая функция является
гармоничной внутри D.
Доказательство:
В силу равномерной сходимости на S справедливо, что
![]()
![]() гармонические и
непрерывные внутри области вплоть до
границы, тогда
гармонические и
непрерывные внутри области вплоть до
границы, тогда
![]()
Воспользовавшись
принципом Коши, получим, что
равномерно
сходится во всех внутренних точках.
![]() Предыдущая функция также будет непрерывна
вплоть до границы
Предыдущая функция также будет непрерывна
вплоть до границы
![]() Выберем внутри D
произвольно М и проведем из м шар радиуса
R,
чтобы он целиком лежал в D,
тогда
Выберем внутри D
произвольно М и проведем из м шар радиуса
R,
чтобы он целиком лежал в D,
тогда
![]()
![]()
При


Применив определение Лапласа к этому выражению получаем, что U(M)=0 U(M) - гармоническая в D, т.к. М произвольная.
Теорема. Если возрастающая последовательность гармонических внутри D функций сходящихся в некоторой внутренней точке области D равномерно
![]() , то она сходится
равномерно в любой замкнутой
, то она сходится
равномерно в любой замкнутой
![]() ,целиком
лежащей в
,целиком
лежащей в
![]() ,
т.е. сходится в любой точке из D.
,
т.е. сходится в любой точке из D.
Доказательство:
![]()
Опишем из сферу радиуса R.
Тогда
![]() по (12)
по (12)
Проведем из другую сферу S’ радиусом R-a, a>0
Будем считать, что
![]() ,тогда внутри этой сферы R_a,
тогда
,тогда внутри этой сферы R_a,
тогда![]() ,
отсюда
,
отсюда
![]()
Выберем
![]() ,
проведем из нее
шар, чтобы он целиком лежал в D
и повторим предыдущее рассуждение. Т.о.
получим сходимость
,
проведем из нее
шар, чтобы он целиком лежал в D
и повторим предыдущее рассуждение. Т.о.
получим сходимость
![]() .
.
По лемме Бореля всякую замкнутую конечную область можно покрыть конечным числом шаров, т.о. это дает равномерную сходимость последовательность в любой замкнутой области, целиком лежащей в D.
Гармоничность предполагаемой функции доказывается аналогично, как в Теореме1.
