3. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Индуктивность длинного соленоида. Энергия магнитного поля. Взаимоиндукция. Трансформация токов и напряжений.

В замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление называют электромагнитной индукцией, а возникающий ток – индукционным. Явление электромагнитной индукции свидетельствует о том, что при изменениях магнитного потока в контуре возникает электродвижущая сила индукции ε_i. Величина ε_i не зависит от способа, которым осуществляется изменение магнитного потока Ф, и определяется лишь скоростью изменения Ф, т.е. dФ/dt.

Закон Фарадея: при изменении потока Ф магнитной индукции через поверхность S, ограниченную замкнутым проводником, в проводнике возникает э.д.с., равная взятой с обратным знаком скорости изменения потока. ε = -dФ/dt.

Правило Ленца. Ленц установил правило, позволяющее найти направление индукционного тока: индукционный тока всегда направлен так, чтобы противодействовать причине, его вызывающей.

Э.д.с. индукции навидится и в незамкнутом проводнике, движущемся в магнитном поле. Сторонние силы вызывают индукционные заряды, электрическое поле которых при равномерном движении проводника в однородном магнитном поле компенсирует сторонние силы: Е = -Е_ст. Индукционные токи наводятся не только в тонких проводниках, но и в массивных сплошных проводниках – токи Фуко.

Электрический ток, текущий в любом контуре, создает пронизывающий этот контур магнитный поток Ψ. При изменениях I изменяется также и Ψ, вследствие чего в контуре индуцируется э.д.с. Если сила тока в проводнике изментяется, то изменяется и поток Ψ, так что в проводнике возникнет э.д.с. согласно закону электромагнитной индукции (ε = -dФ/dt). Возникновение э.д.с. в проводнике вследствие изменения силы тока в самом проводнике называется самоиндукцией.

ε_сам = -L∙dI/dt.

В соответствии с законом Био-Савара магнитная индукция В пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток I в контуре и создаваемый им полный магнитный поток Ψ через контур пропорциональны друг другу: Ψ = LI. Коэффициент пропорциональности L между силой тока и полным магнитным потоком называется индуктивностью контура.

Индуктивность длинного соленоида. Возьмем соленоид такой длины, чтобы его можно было считать практически бесконечным. При протекании по нему тока I внутри соленоида возбуждается однородное поле, индукция которого равна В = μ₀μnI. Поток через каждый из витков равен Ф = ВS, а полный магнитный поток, сцепленный с соленоидом, Ψ = NФ = nlBS = μ₀μn²lSI.

L = μ₀μn²lS = μ₀μn²V.

Для двух контуров, по которым текут токи I₁ и I₂, можно показать, что коэффициент пропорциональности (Ф = LI) зависит от геометрических свойств контуров и их взаимного расположения. Это коэффициент взаимной индукции, а о контурах при не равном 0 коэффициенте взаимной индукции говорят как об индуктивно связанных друг с другом. При изменении силы тока в одном из индуктивно связанных контуров в другом возникает э.д.с. – явление взаимной индукции.

Энергия магнитного поля. Рассмотрим цепь, состоящую из источника постоянного тока, сопротивления и катушки индуктивностью L, в которой течет ток силой I. Предположим, что в некоторый момент времени действие сторонних сил источника прекращается. Вследствие явления самоиндукции ток в цепи исчезнет не сразу, поскольку э.д.с. самоиндукции будет по правилу Ленца препятствовать убыванию силы тока, т.е. поддерживать убывающий ток. В процессе убывания тока сторонние силы, ответственные за э.д.с. самоиндукции, совершают работу над носителями тока. За малый промежуток времени dt сторонние силы совершают работу dA = ε_самdq, где dq = Idt.

Т.о. dA = -LIdI. Полная работа получается суммированием малых работ, совершаемых в течение всего процесса исчезновения тока. По закону сохранения энергии эта работа определяет энергию W, которой обладает катушка с током: W = LI²/2. Эту энергию следует приписать магнитному полю соленоида. Считая соленоид достаточно длинным, можно полагать, что поле целиком сосредоточено внутри соленоида и однородно. W = VB²/2μ₀μ.

4. Переменный электрический ток. Закон Ома для цепей переменного тока. Мощность переменного тока.

Под переменным током будем понимать синусоидальный ток: I = I₀sin(ωt+φ).

Закон Ома для участка цепи с сопротивлением R. Пусть на участке цепи с сопротивлением R и пренебрежимо малыми емкостью и индуктивностью течет переменный синусоидальный ток силой I = I₀sinωt. Для мгновенных значений силы тока и напряжения верен закон Ома:

U_R(t) = RI(t) = RI₀sinωt. Следовательно напряжение U_R совершает гармоническое колебание с теми же частотой и фазой, что и сила тока, а амплитудные значения силы тока и напряжения связаны соотношением: U_R0 = RI₀.

Закон Ома для участка цепи с емкостью. Рассмотрим участок цепи, емкость которого С, а сопротивление и индуктивность пренебрежимо малы, по которому течет ток силой I = I₀sinωt.

q = ∫Idt = ∫I₀sinωtdt = -I₀ cosωt/ω = I₀ sin(ωt-π/2)/ω.

Тогда U_C(t) = I₀ cosωt/ωC. Т.е. напряжение совершает гармонические колебания с той же круговой частотой ω, но отстает по фазе от силы тока на π/2, причем амплитудные значения связаны соотношением: U_C0 = I₀ /ωС. Сравнивая этот закон с обычным законом Ома заметим, что R_C = 1/ωС – емкостное сопротивление.

Закон Ома для участка цепи с индуктивностью. Рассмотрим участок цепи с индуктивностью L и пренебрежимо малыми сопротивлением и емкостью, по которому течет ток силой I = I₀sinωt. Тогда U_L = LdU/dt = Ld(I₀sinωt)dt = ωLI₀cosωt = ωLI₀ sin(ωt+π/2). Т.о. напряжение на индуктивности также совершает гармонические колебания с круговой частотой ω, но опережает по фазе силу тока на π/2, причес амплитудные значения силы тока и напряжения связаны соотношением: U_L0 = ωLI₀, а величина R_L = ωL – индуктивное сопротивление.

Емкостное и индуктивное сопротивления – реактивные.

Закон Ома для всей цепи. Рассмотрим теперь участок цепи, состоящий из последовательно соединенных резистора с активным сопротивлением R, конденсатора емкостью С и катушки индуктивностью L с пренебрежимо малым сопротивлением проводов, по которому течет ток силой I = I₀sinωt. Тогда напряжение на участке складывается из напряжений: U = U_R + U_C + U_L. Суммарное напряжение будет гармоническим колебанием той же частоты.

Энергия и мощность в цепи переменного тока. ΔА^ст = ΔQ + ΔW_э + ΔW_м – работа сторонних сил на выделение теплоты ΔQ, а также на приращение энергии электрического поля конденсатора ΔW_э и магнитного поля катушки ΔW_м. Мощность источника тока – работа сторонних сил в единицу времени Р_ε = dА^ст/dt.

Р_ε = Р_R + Р_C + Р_L, где Р_ε = Iε, Р_R = IU_R, Р_C = IU_C, Р_L = IU_L.

Т.к. I = I₀sinωt, то Р_R = I₀U_R0sin²ωt , Р_C = I₀U_C0sin(2ωt-π)/2 , Р_L = I₀U_L0sin2ωt.

5. Электромагнитные колебания. Дифференциальное уравнение собственных электромагнитных колебаний в контуре. Затухающие колебания. Добротность контура. Вынужденные колебания. Резонанс напряжений и токов.

Свободные электрические колебания. Основное дифференциальное уравнение колебательного контура: L∙d²q/dt² + R∙dq/dt + q/C = 0.

Механические колебания	Электрические колебания
Уравнение
m∙d2x/dt2 + b∙dx/dt + kx = 0	L∙d2q/dt2 + R∙dq/dt + q/C = 0
Координата x(t)	Заряд q(t)
Масса m	Индуктивность L
Коэффициент трения b	Сопротивление R
Коэффициент жесткости k	Величина 1/С, обратная емкости
Решение
x(t) = Ae-βtcos(ωt+φ)	q(t) = Ae-βtcos(ωt+φ)
где коэффициент затухания
β = b/2m	β = R/2L
круговая частота
ω = √ω02–β2	ω = √ω02–β2
ω0 = k/m	ω0 = 1/√LC

При не слишком большом затухании заряд на конденсаторе изменяется со временем по закону затухающего колебания q(t) = Ae^-βtcos(ωt+φ). Сходным образом вдует себя и переменные электрические величины в контуре I(t), U_R(t),U_C(t),U_L(t). Такие электрические колебания называются свободными, т.к. они происходят при отсутствии внешних воздействий.

В идеальном контуре R=0 коэффициент затухания β обращается в нуль и колебания становятся гармоническими.

q(t) = q₀cosωt, I(t) = dq/dt = q₀ω₀cos(ω₀t + π/2), U_C(t) = q/C = q₀cos(ω₀t)/C,

U_L(t) = L∙dI/dt = q₀Lω₀²cos(ω₀t + π).

Поскольку источник отсутствует, то -ΔQ = Δ(W_э + W_м). Энергия в процессе колебаний лишь перераспределяется со временем между конденсатором и катушкой, сохраняя свое полное значение.

Вынужденные электрические колебания. На контур оказывается внешнее воздействие, например, посредством включения последовательно с элементами контура источника напряжения с э.д.с., изменяющейся по закону гармонического колебания ε = ε₀sinωt.

Механические колебания	Электрические колебания
Уравнение
m∙d2x/dt2 + b∙dx/dt + kx = f0sinωt	L∙d2q/dt2 + R∙dq/dt + q/C = ε0sinωt
Решение
x(t) = Asin(ωt+φ)	q(t) = q0sin(ωt+φ)

I = dq/dt = q₀ωcos(ωt + φ + π/2), U_R = RI = q₀ωRsin(ωt + φ + π/2), U_C = q/C = q₀sin(ωt + φ)/C,

U_L = L∙dI/dt = q₀Lω²sin(ωt + φ + π).

Для вынужденных колебаний характерно явление резонанса, которое заключается в возрастании амплитуды вынужденных колебаний при приближении частоты внешнего воздействия к резонансной частоте, зависящей от параметров колебательной системы (R, C, L).

Добротность. Q = √(L/C)/R – добротность контура. Добротность пропорциональна логарифмическому декременту затухания λ: Q = π/λ. Добротность обратно пропорциональна относительной убыли энергии Δ_TW/W контура за период свободных колебаний: Q = 2πW/Δ_TW.

Добротность показывает, во сколько раз амплитуда напряжения на конденсаторе при резонансе больше амплитуды ε₀ э.д.с. источника напряжения: Q = U_С0^рез/ε₀. Добротность равна ширине резонансной кривой: Q = ω₀/Δω. Шириной резонансной кривой или полосой пропускания нахывают интервал частот Δω, ограниченный частотами, на которых амплитуда в √2 раз меньше, чем при резонансе.

6. Электромагнитное поле. Вихревые электрические и потенциальные магнитные поля. Ток смещения. Уравнения Максвелла в интегральной форме. Электромагнитные волны и их свойства. Шкала электромагнитных волн.

Электромагнитное поле - 1) это совокупность электрических и магнитных полей, которые могут переходить друг в друга. Математически этот процесс описывается в электродинамике посредством системы уравнений Максвелла.

- 2) это область пространства, в которой наблюдаются электромагнитные взаимодействия (например пробного заряда в конкретной точке пространства с этим полем).

Вихревое электрическое поле – поле, у которого все линии напряженности электрического поля замкнуты (вихревым также является постоянное магнитное поле).

Потенциальное поле - консервативное поле, векторное поле, циркуляция которого вдоль любой замкнутой траектории равна нулю.

Ток смещения – такой ток, который порождает то же магнитное поле, которое порождается переменным электрическим полем. Ток проводимости – поток заряженных частиц. j_полн=j+j_см, где j_полн – плотность полного тока в каждой точке пространства.

▼j=-δp/δt, где р – плотность заряда, t – время.

Уравнения Максвелла – система 4 (дополненных 3-мя убогими нижними формулами, последняя из которых – закон Ома) уравнений, описывающая все классические (неквантовые) электромагнитные явления:

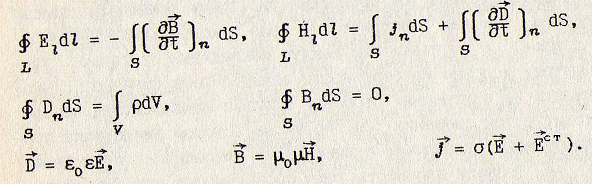
Верхние формулы – обобщённые теоремы о циркуляциях (1 – всякое, изменяющееся во времени магнитное поле порождает в пространстве электрическое поле, 2 – переменное электрическое поле порождает магнитное), средние – теоремы о потоках, остающиеся справедливыми в общем случае переменных полей, 1 – теорема Гаусса для диэлектрика: поток электрического смещения через любую замкнутую поверхность равен сумме сторонних зарядов, заключённых внутри поверхности, 2 – теорема о потоке: поток магнитной индукции через любую замкнутую поверхность S равен 0.

Электромагнитные волны — это плоско поляризованные поперечные волны (волны сдвига), в которых вектора напряжённостей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны, существенно отличаются от волн на воде и от звука тем, что их можно передать от источника к приемнику в том, числе через вакуум.

Э.М.В. испускаются только ускоренно движущимися зарядами или, что то же самое, переменными токами. Интенсивность излучения зависит не только от ускорения зарядов, но и конфигурации системы.

Формула монохроматической волны в однородной нейтральной диэлектрической среде:

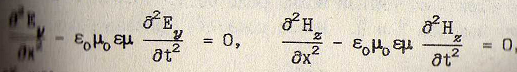
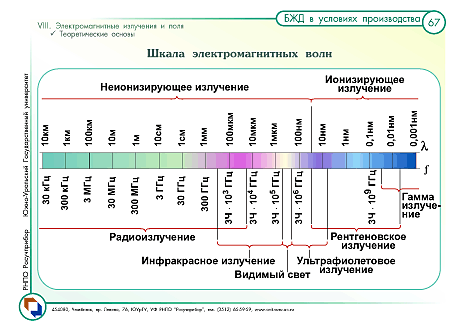
Шкала электромагнитных волн.

Частота (гц)	Длина волны (м)	Название диапазона	Основные методы генерации	Область применения
До 10	Более 3 10	Низкочастотные Колебания	Генераторы переменного тока (искусственные вибраторы)	электротехника
10	3 10	Радиоволны	Генераторы радиочастот Генераторы СВЧ	Радиотехника, радиосвязь, телевидение, радиолокация
10	3 10	Инфракрасное излучение	Излучение молекул и атомов при тепловых и электрических воздействиях	Тепловые и фотографические теплицы, глаз, фотография, фотоэлектрическая жизнь на Земле
3,8 10	8 10	Световые волны (видимый свет)	То же	То же
7,5 10	4 10	Ультрафиолетовое излучение	Излучение атомов при воздействии ускоренных электронов	Фотография, фотоэлектрическая медицина
3 10	10	Рентгеновское излучение	То же	То же
3 10	10	Рентгеновское и Альфа-излучение	Атомные процессы  при воздействии Ускоренных заряженных частиц (возникает в результате изменения состояний электронов на внутренних оболочках атома или в результате резкого торможения электронов и др. заряженных частиц)	Фотография, ионизационные медицина и металлургия
10	3 10	Альфа- излучения	Возбуждение ядра атомов и элементарные  частицы в результате различных взаимодействий: радиоактивный распад, ядерные процессы, космические процессы	Ионизационный метод меченых атомов

13