Розділ 5 оптимальне планування і координація управління виробництвом в нечітких умовах

5.1 Методи вирішення задач планування в нечітких умовах

Серед питань, що вирішуються при розробці автоматизованих систем управління, проблема побудови адекватної моделі планування і вибору прийнятних алгоритмів рішення є одна з найважливіших і найскладніших. Важливість цього питання походить з того факту, що від правильної побудови моделі і вибору ефективного алгоритму рішення задачі планування залежить нормальне функціонування виробництва.

Планування виробничої програми промислового підприємства здійснюється, як правило, в умовах неточності початкової інформації, коли деякі системні параметри визначаються недостатньо точно, що породжує невизначеність умов планування. Часто цю невизначеність не можна розглядати як стохастичне явище, оскільки відсутні стохастичні параметри і вона може характеризуватися швидше нечіткими категоріями, залежними від кількості і якості сировини, термінів його постачання; функціонування технологічних установок (зокрема, пов’язаною з можливими змінами коефіцієнтів залучення і відбору); термінів початку і кінця ремонтних робіт; втрат продуктів, неточності датчиків і так далі.

У зв’язку з вищезгаданим виникає інтерес до теорії нечітких множин для вирішення завдань планування. В даний час накопичений певний досвід [29 – 43], в якому можна виділити два напрями:

застосування нечіткої логіки [5, 10, 29, 30, 32, 34, 43];

застосування нечіткого лінійного програмування [9, 18, 31 – 33, 35-42].

Застосування нечіткої логіки засноване на наступному. Множина входів А і виходів В системи розбиваються на підмножини і що описуються лінгвістичними термами малий, середній, великий і так далі. Між ними встановлюються бінарні нечіткі відносини , які визначаються як:

(5.1)

На основі правила композиційного виводу можна, знаючи вхід системи, визначити значення на виході:

. (5.2)

У [29] розглядається завдання планування виробництва з безперервною технологією, в якій елементи вектора обмежень на виробничі ресурси є нечіткими і задані у вигляді інтервалів . На універсальній множині будують нечіткі підмножини, що описуються первинними лінгвістичними термами малий, середній, великий і так далі з відповідними функціями приналежності. Потім, використовуючи положення нечіткої логіки вигляду IFATHENB і правила композиційного виводу, шукають рішення поставленої задачі. Це рішення представляється ЛПР, і той приймає його або змінює пріоритет окремих обмежень і вирішує задачу наново.

У [32] розглянуто багатокритеріальне завдання планування роботи гідротермальної енергетичної станції з обмеженнями на ввідні ресурси і трьома цільовими функціями: мінімізація витрат, повне використання виробленої енергії, стабілізація рівня в резервуарах. На підставі лінгвістичної інформації, отриманої від ЛПР, безліч значень контрольованих параметрів розбиваються на підмножини, що описуються лінгвістично, і на основі нечіткої логіки визначають «чинники зміни ваг», а потім вирішують задачу скалярної оптимізації. В ході діалогу з ЛПР послідовно змінюються ці ваги і задачу вирішують наново до тих пір, поки цільові функції не приймуть задовільні значення ЛПР.

У [43] вирішується завдання управління запасами. На підставі наявної інформації будують функції приналежності нечітких цілей і обмежень і ведуть пошук такого рішення, яке максимізувало функцію приналежності перетину множини цілей і множини обмежень.

Застосування даного підходу вельми зручне і перспективне, проте збільшення розмірності системи веде до ускладнення і трудності реалізації даного алгоритму.

Зупинимося на деяких підходах до вирішення завдань планування на основі нечіткого лінійного програмування (НЛП).

Нечітка модель завдання планування може бути записана у вигляді:

(5.3)

де F – цільова функція; C – вектор цін; – вектор iнтен-сивностi технологічних способів виробництва; А – матриця технологічних коефіцієнтів; В – вектор-стовпець виробничих ресурсів; ~ – означає нечіткість.

У [35 – 36] розглядається модель:

(5.4)

де – деяке бажане для ЛПР значення цільової функції.

Далі будують лінійні функції приналежності що відображають ступінь виконання і-го обмеження у вигляді:

(5.5)

і вирішують задачу знаходження:

(5.6)

що еквівалентно вирішенню наступної задачі:

(5.7)

Тут – величина на яку може бути порушене обмеження.

У [36] пропонується модифікувати запропонований вище метод, використавши замість лінійних функцій приналежності – гіперболічні:

, (5.8)

де – значення j-ї цільової функції в оптимальній для неї точці , а

. (5.9)

Використовуючи формулу гіперболічного тангенса, і підставляючи

(5.10)

приходимо до вигляду:

(5.11)

Трохи інакше розглядається завдання НЛП в [37].

Обмеження

ціль (5.12)

Нечіткими пропонуються параметри А, В, С, K, і вони визначаються своїм центром а і шириною с, тобто функція приналежності нечіткого числа записується як:

(5.13)

Нечітка функція має вигляд F

(5.14)

де – є множина всіх нечітких підмножин в Y.

Тоді, не роблячи відмінностей між цілями і обмеженнями, можна записати:

(5.15)

(5.16)

(5.17)

і завдання зводиться до вигляду

(5.18)

де – бажане значення відповідного обмеження; h – параметр.

Для вирішення цього завдання нелінійного програмування розроблений спеціальний алгоритм.

У [18, 32, 38] для вирішення завдань НЛП використовується поняття -рівнів. Тут необхідно вирішити N завдань лінійного програмування, де N – число -рівнів.

У [11] розглядаються різні типи нечітких обмежень, на основі RL – представлення нечітких чисел: нечітке число може бути представлене трійкою параметрів , де m – середнє значення, і – відповідно ліве (нижнє) і праве (верхнє) відхилення.

Функція приналежності

(5.19)

де L і R – симетричні колоподібні функції, такі, що ; називають числом RL-типу (рис. 5.1).

1. Система толерантних обмежень. Завдання нечіткого лінійного програмування (ЗНЛП) має вигляд:

(5.20)

Це завдання еквівалентне наступним чітким:

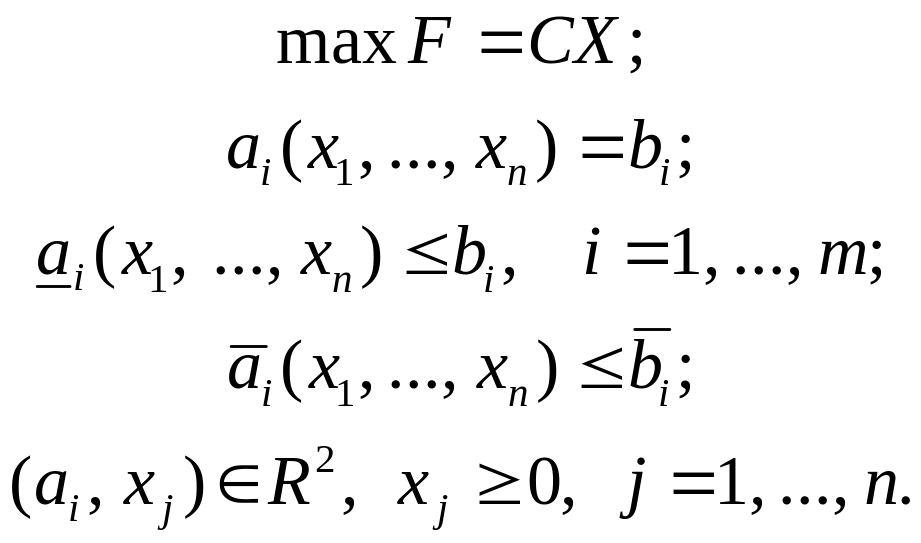(5.21)

2. Система толерантних обмежень, що включають нечіткі змінні. Ставиться завдання:

(5.22)

Необхідно знайти максимально допустиму розмитість при даних таких, що могло бути досягнуте за допомогою і . Передбачається, що всі нечіткі числа позитивні, RL-типу. Ця система еквівалентна:

(5.23)

3. Система наближеної рівності. Розглядається завдання

(5.24)

Чітка модель має вигляд

(5.25)

По даному класу завдань планування необхідно зробити наступне зауваження. Якщо в первинному завданні є т обмежень, то у випадках 1 і 2 число обмежень буде 3m, а у разі 3 – 2т. Включення у випадки 1 і 2 обов’язкова рівність по середніх значеннях зменшує гнучкість моделі.

Завдання планування виробництва в деревообробній промисловості вирішене в [41]. Тут мова йде про багатокритерійному завданні наступного вигляду:

(5.26)

Функція приналежності

(5.27)

тоді завдання

(5.28)

може бути вирішена стандартними прийомами.

У [42] описано завдання мінімізації числа потрібних для виробництва продукції машин. Пропонується наступна модель:

(5.29)

Доводиться, що існує вектор такий, що рішення задачі

(5.30)

є в той же час рішення поставленої задачі. Тут – міцність множини X.

Приводиться також модель наближеного розподілу ресурсів і багатокритерійна неопукла модель виробничої програми. Для вирішення останньою запропоновано використовувати алгоритм Falk – Soland, який при використанні методу гілок і меж дозволяє отримати послідовність допустимих крапок, що є вирішенням ряду підзадач.

Розглянемо підхід рішенню задачі планування в нечіткому середовищі, заснований на LR-представленні нечітких множин, але що відрізняється від описаних в літературі.

Введемо наступні визначення.

Визначення 5.1. Нечітке число менше нечіткого числа (рис. 5.2), якщо

(5.31)

Визначення 5.2. Нечітке число більше нечіткого числа , якщо

. (5.32)

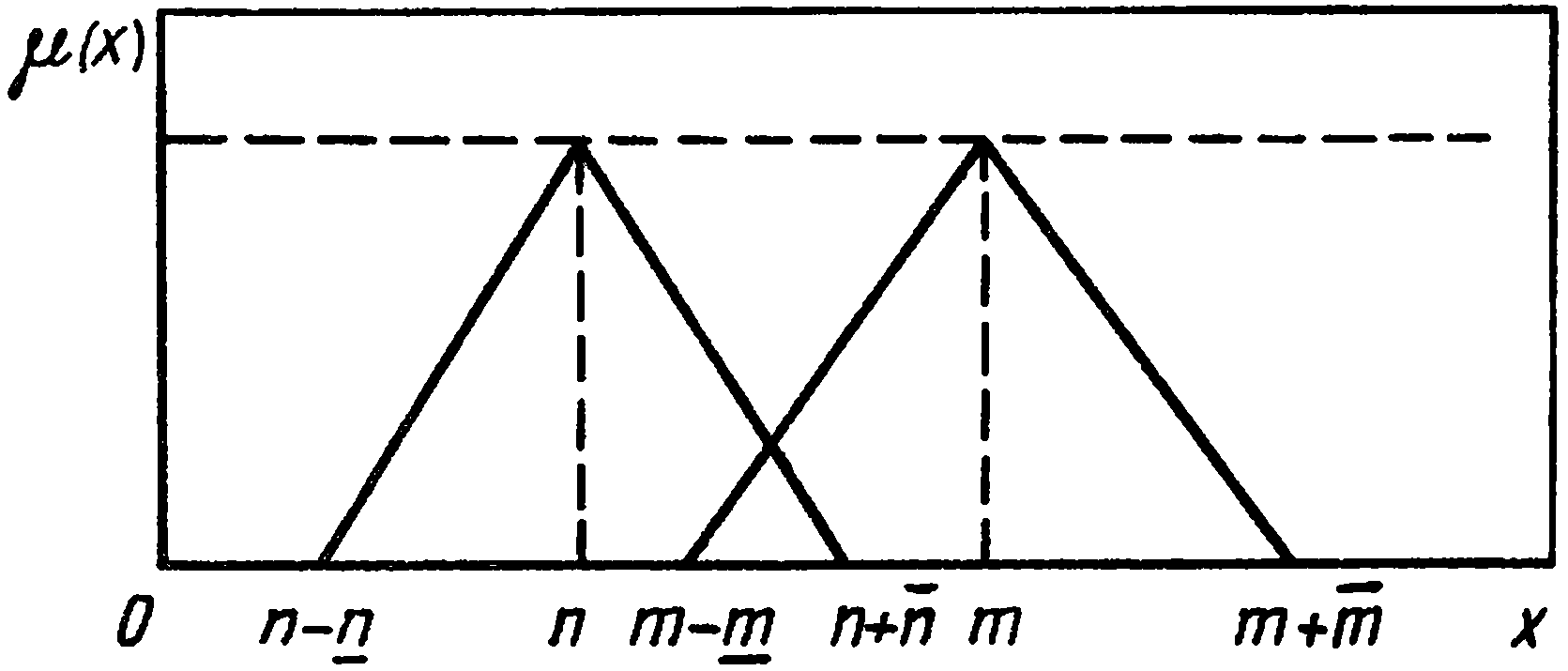
Рисунок 5.2 – Функція приналежності нечіткого числа

Визначення 5.3. Нечітке число рівне нечіткому, числу , якщо

. (5.33)

На підставі визначень (5.31) – (5.33) перейдемо до чіткого аналога системи (5.3):

(5.34)

Агрегуючи змінні

(5.35)

декомпозуємо (5.34) на наступні системи:

(5.36)

(5.37)

. (5.38)

У системи (5.37) і (5.38) введені додаткові обмеження, що відображають той факт, що повинне виконуватися нерівність:

(5.39)

де х* – оптимальне вирішення системи (5.36).

Вирішивши системи (5.36) – (5.38), визначимо значення х*, х’*, х"*.

Тоді нечітке рішення задачі (5.3) в RL-зображенні (рис. 5.3) запишемо як

. (5.40)

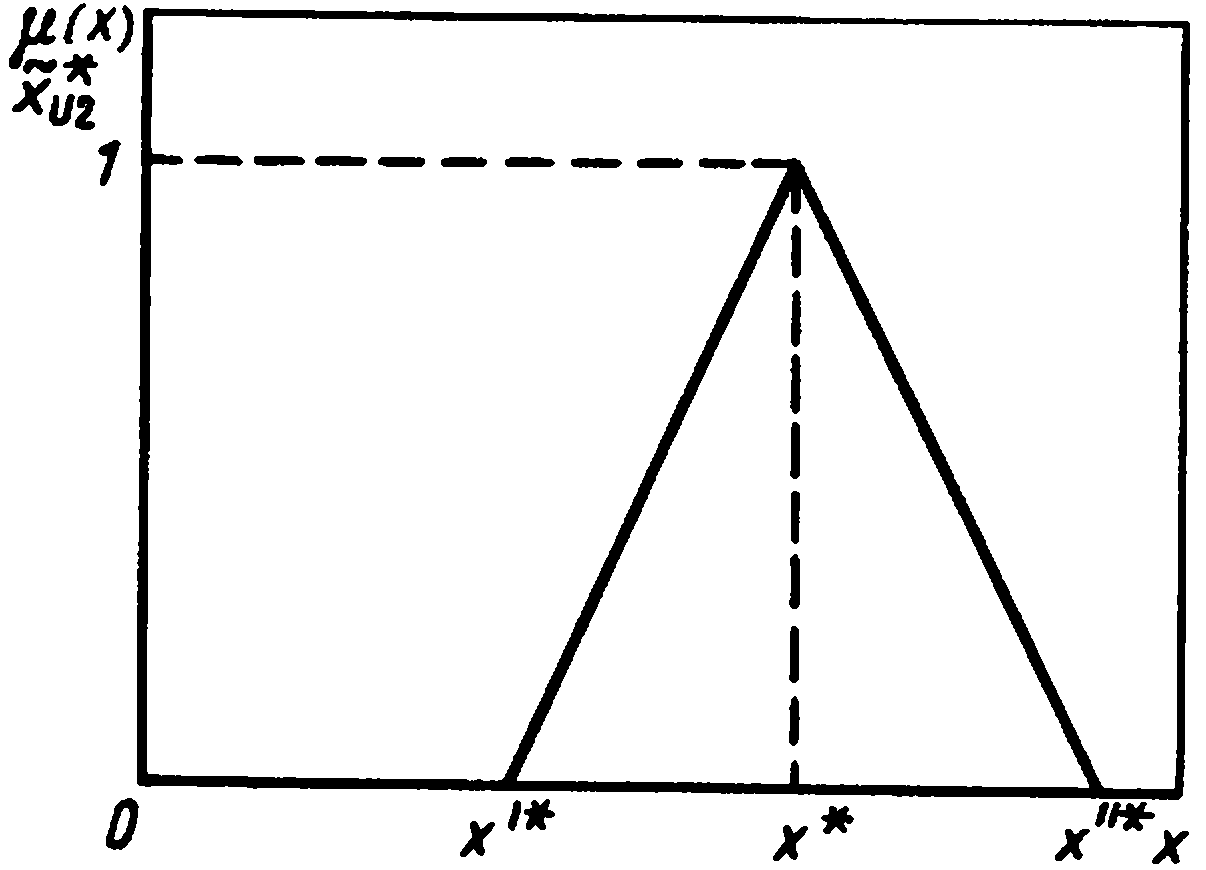
Рисунок 5.3 – Нечітке рішення задачі оптимізації при RL-представленні

Якщо нижнє і верхнє відхилення вектора пропорційні середньому значенню, то справедлива наступна теорема.

Теорема 5.1. Якщо для нечіткого числа виконується умова:

(5.41)

і система (5.36) має рішення х*, то (5.37) і (5.38) мають рішення:

. (5.42)

Доведення. Нехай (5.36) має рішення х*. Розіб’ємо матрицю А на дві підматриці (за умови ): Б – квадратну і N – розмірністю :

. (5.43)

Розіб’ємо змінні і вектор цін відповідно:

(5.44)

Тоді запишемо:

. (5.45)

звідки

. (5.46)

Значення функціонала

. (5.47)

Як відомо, умова допустимості має вигляд

. (5.48)

Враховуючи, що в оптимальному рішенні небазисні змінні рівні нулю, умова (5.48) буде мати вигляд

. (5.49)

Умову оптимальності запишемо як

. (5.50)

Як видно з (5.49), (5.50), зміна правої частини приведе до зміни лише умови допустимості (5.48).

Запишемо в аналогічному вигляді рішення задачі (5.36):

(5.51)

але Так як – допустиме рішення (5.36) і то Звідси випливає, що

Думаючи аналогічно, отримаємо:

(5.52)

що і потрібно було доказати.

В цьому випадку для отримання нечіткого розв’язку системи (5.3) достатньо получити розв’язок системи (5.36), а розв’язок систем (5.37) і (5.38) можна розраховувати по (5.40).