
- •Глава 3. Кодирование символьной информации
- •3.1. Постановка задачи кодирования. Первая теорема Шеннона
- •3.2. Способы построения двоичных кодов 3.2.1. Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды
- •3.2.2. Равномерное алфавитное двоичное кодирование. Байтовый код
- •3.2.3. Алфавитное кодирование с неравной длительностью элементарных сигналов. Код Морзе
- •3.2.4. Блочное двоичное кодирование
- •Глава 6. Кодирование
- •6.1 Алфавитное кодирование
- •6.1.1. Префикс и постфикс слова
- •6.1.2. Таблица кодов
- •6.1.3. Разделимые схемы
- •6.1.4. Префиксные схемы
- •6.1.5. Неравенства Макмиллана
- •6.2. Кодирование с минимальной избыточностью
- •6.2.1. Минимизация длины кода сообщения
- •6.2.2. Цена кодирвания
- •6.2.3. Алгоритм Фано
- •6.2.4. Оптимальное кодирование
- •6.2.5. Алгоритм Хаффмана
- •6.3. Помехоустойчивое кодирование
- •6.3.1. Кодирование с исправлением ошибок
- •6.3.2. Классификация ошибок
- •6.3.3. Возможность исправления всех ошибок
- •6.3.4. Кодовое расстояние
6.2.3. Алгоритм Фано
Следующий рекурсивный алгоритм строит разделимую префиксную схему алфавитного кодирования, близкого к оптимальному.
Алгоритм 6.1. Построение кодирования, близкого к оптимальному
Вход: P : array
[1..n] of real
– массив вероятностей появления УКВ в
сообщении, упорядоченный по невозрастанию;
![]() .
.
Выход: C : array [1..n, 1..L] of 0..1 – массив элементархых кодов.
Fano (1, n, 0) { вызов рекурсивной процедуры Fano }
Основная работа по построению элементарных кодов выполняется следующей рекурсивной процедурой Fano.
Вход: b – индекс начала обрабатываемой части массива P, е – индекс конца обрабатываемой части массива P, к – длина уже построенных кодов в обрабатываемой части массива С.
Выход: заполненный массив С.
if e > b then
k:=k+1 { место для очередного разряда в коде }
m:=Med (b, e) { деление массива на две части }
for I from b to e do
C [i,k] := I > m { в первой части добавляем 0, во второй - 1 }
end for
Fano (b, m, k) { обработка первой части }
Fano (m+1, e, k) { обработка второй части }
end if
Функция Med находит медиану
указанной части массива P
[b..e], то есть
определяет такой индекс m
(![]() ),
что сумма элементов P
[b..m] наиболее
близка к сумме элементов P
[m+1..e].
),
что сумма элементов P
[b..m] наиболее
близка к сумме элементов P
[m+1..e].
Вход: b – индекс начала обрабатываемой части массива P, e – индекс концап обрабатываемой части массива P.
Выход: m – индекс медианы,
то есть
![]()
Sb:= {сумма элементов первой части }
for i from b to e-1 do
Sb:=Sb+P[i] { вначале все, кроме последнего }
end for
Se:=P[e] { сумма элементво второй части }
M := e { начинаем искать медиану с конца }
repeat
d:=Sb-Se { разность сумм первой и второй части }
m:=m-1 { сдвигаем границу медианы вниз }
Sb:=Sb-P[m];
Se:=Se+P[m]
until |Sb-Se| d
return m
Обоснование
При каждом удлинении кодов в одной части коды удлиняются нулями, а в другой – единицами. Таким образом, коды одной части не могут быть префиксами другой. Удлинение кода заканчивается тогда и только тогда, когда длина части равна 1, то есть остается единственный код. Таким образом, схема по построению префиксная, а потому разделимая.
Пример
Коды, построенные алгоритмом Фано для заданного распределения (n=7).
pi |
C[i] |
li |
0.20 |
00 |
2 |
0.20 |
010 |
3 |
0.19 |
011 |
3 |
0.12 |
100 |
3 |
0.11 |
101 |
3 |
0.09 |
110 |
3 |
0.09 |
111 |
3 |
|
|
2.80 |
6.2.4. Оптимальное кодирование
Оптимальное кодирование обладает определенными свойствами, которые можно использовать для его построения.
ЛЕММА Пусть
- схема оптимального кодирования для
распределения вероятностей
![]() .
Тогда если pi>pj,
то
.
Тогда если pi>pj,
то
![]() .
.
Доказательство
От противного. Пусть i<j, pi>pj и li>lj. Тогда рассмотрим
![]()
Имеем:
![]()
что противоречит тому, что оптимально.
Таким образом, не ограничивая общности,
можно считать, что
![]() .
.
ЛЕММА
Если - схема оптимального префиксного кодирования для распределения вероятностей , то среди элементарных кодов, имеющих максимальную длину, имеются два, которые различаются только во последнем разряде.
Доказательство
От противного
Пусть кодовое слово максимальной длины одно и имеет вид
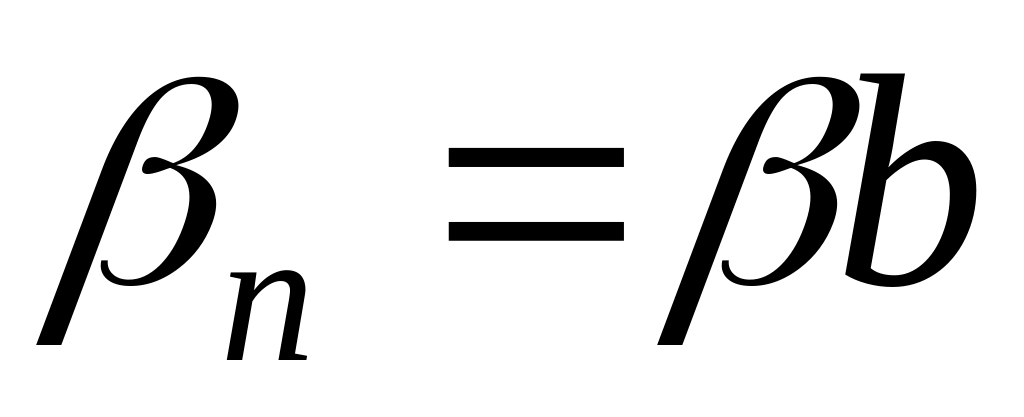 ,
где b=0 V
b=1. Имеем:
,
где b=0 V
b=1. Имеем:
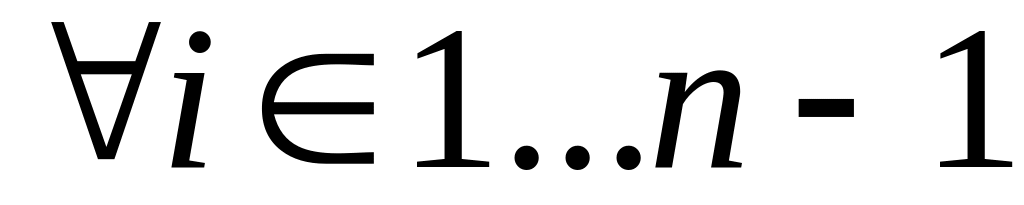
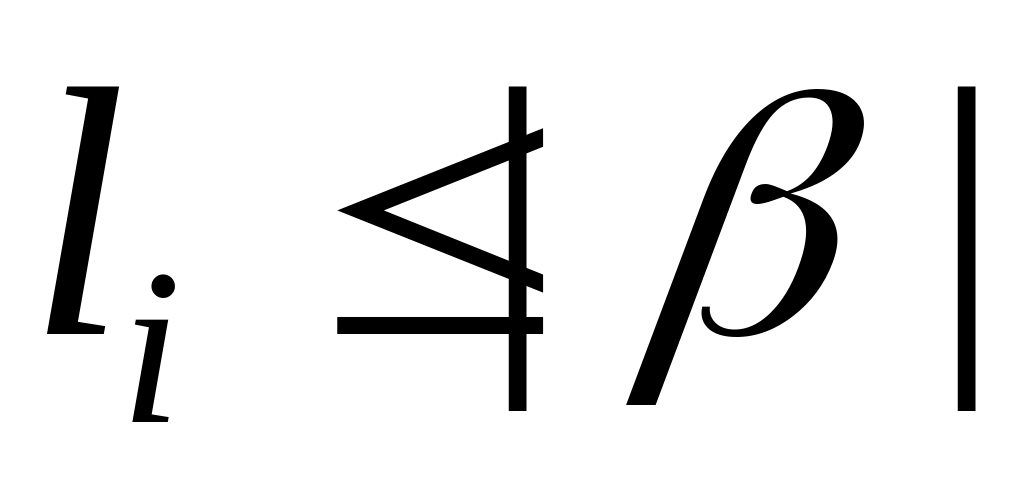 .
Так как схема префиксная, то слова
.
Так как схема префиксная, то слова
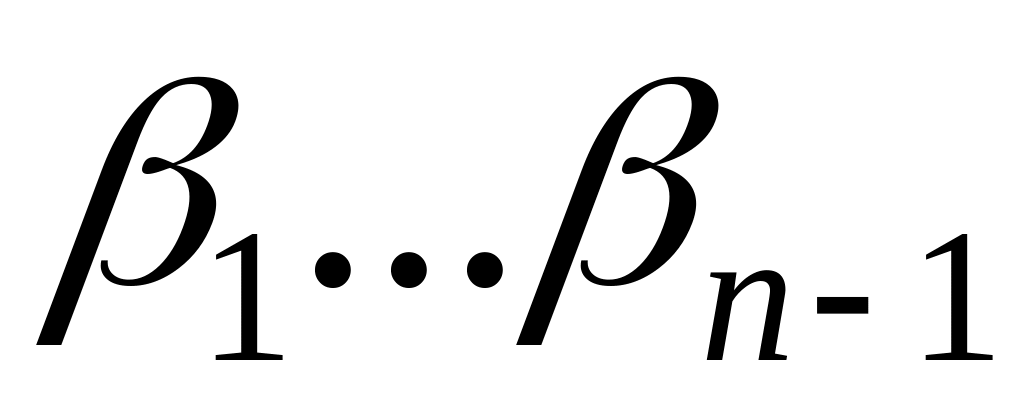 не являются префиксами
не являются префиксами
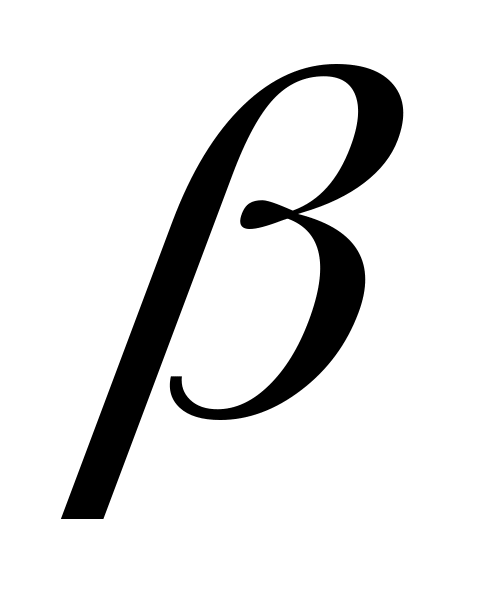 .
С другой стороны,
не является префиксом слов
,
иначе было бы
.
С другой стороны,
не является префиксом слов
,
иначе было бы
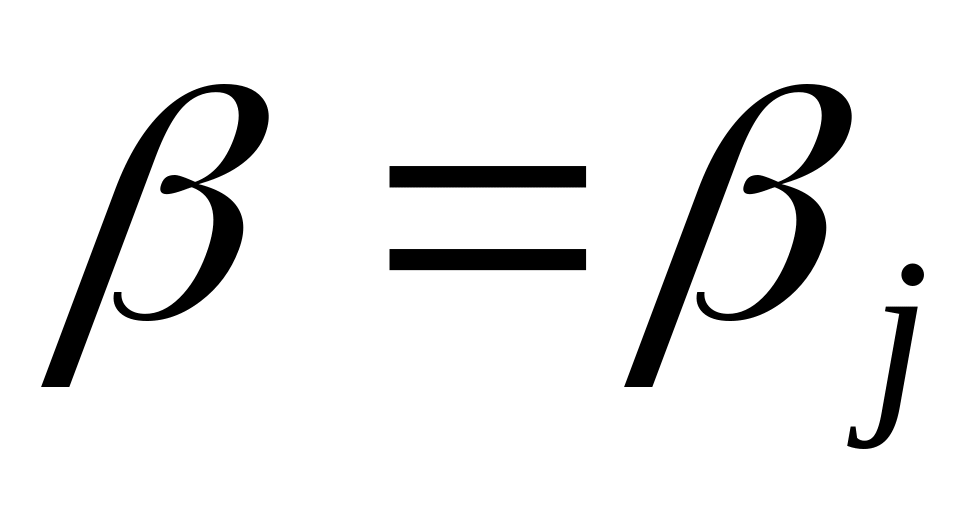 ,
а значит,
,
а значит,
 было бы префиксом
было бы префиксом
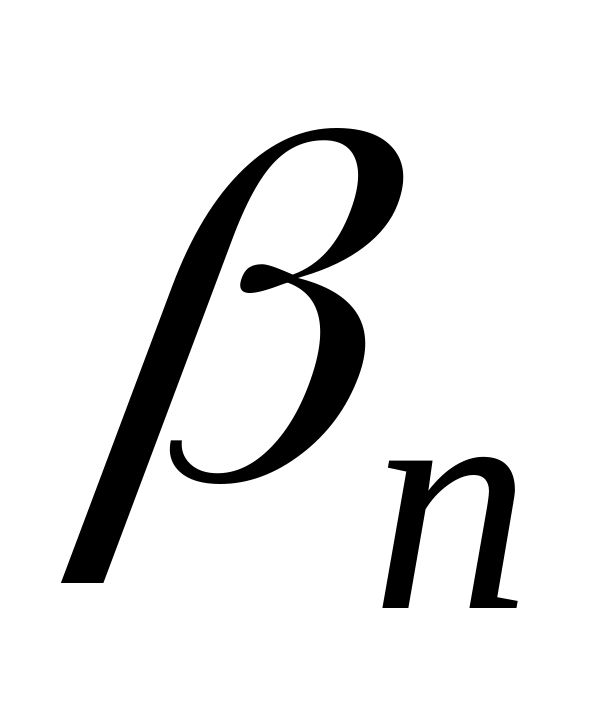 .
Тогда схема
.
Тогда схема
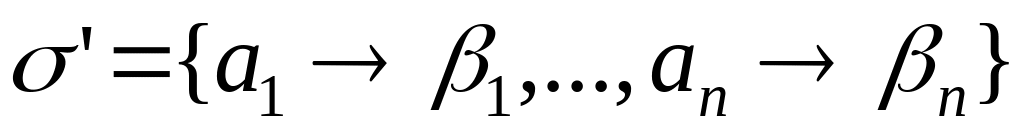 тоже префиксная, причем
тоже префиксная, причем
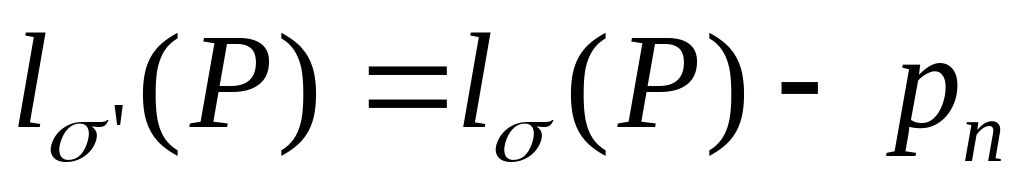 ,
что противоречит оптимальности
.
,
что противоречит оптимальности
.Пусть теперь два кодовых слова
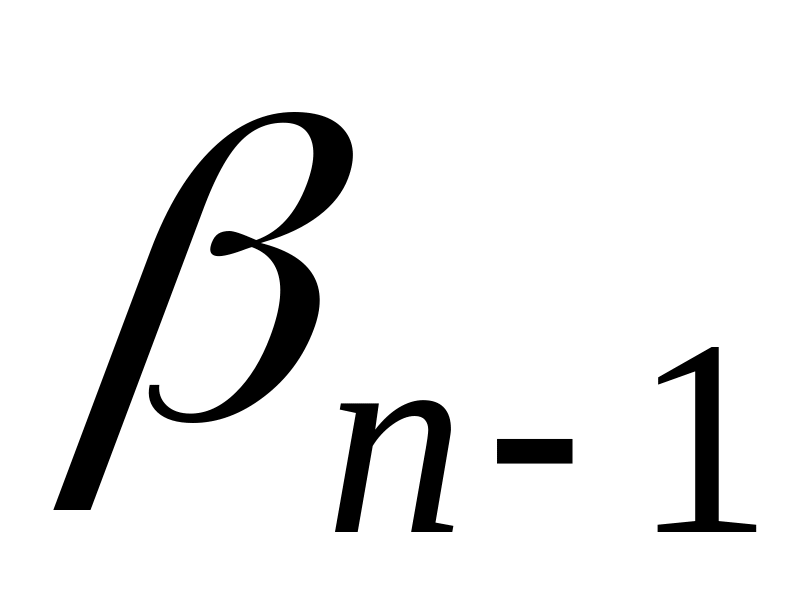 и
и
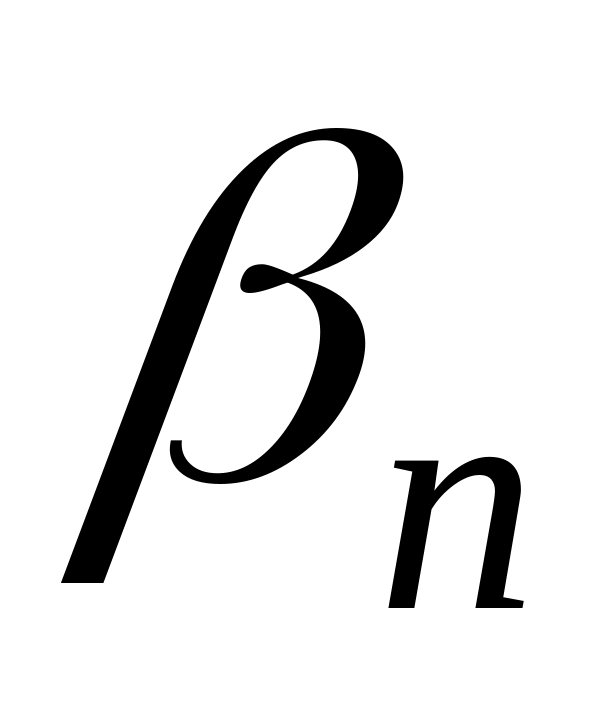 максимальной длины отличаются не в
последнем разряде, то есть
максимальной длины отличаются не в
последнем разряде, то есть
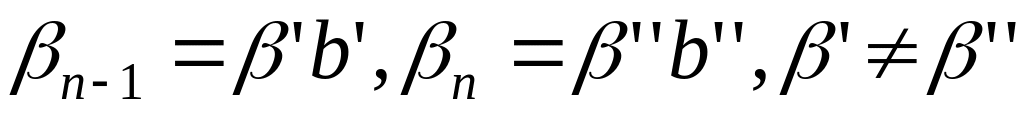 ,
причем
,
причем
 не являются префиксами для
не являются префиксами для
 и наоборот. Тогда схема
и наоборот. Тогда схема
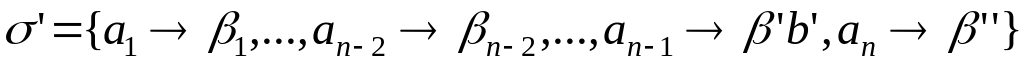 также является префиксной, причем
,
что противоречит оптимальности
.
также является префиксной, причем
,
что противоречит оптимальности
.
ТЕОРЕМА Если
![]() - схема оптимального префиксного
кодирования для распределения вероятностей
- схема оптимального префиксного
кодирования для распределения вероятностей
![]() и
и
![]() ,
причем
,
причем
![]() ,
,
то кодирование со схемой
![]()
является оптимальным префиксным кодированием для распределения вероятностей Pn=p1,…,pj-1,pj+1,…,pn-1,q’,q’’.
Доказательство
Если
 было префиксным, то
было префиксным, то
 тоже будет префиксным по построению.
тоже будет префиксным по построению.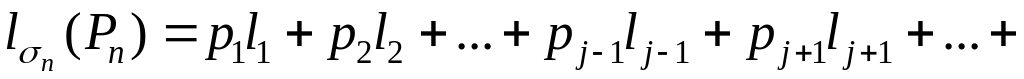
![]()
![]()
![]()
Пусть схема
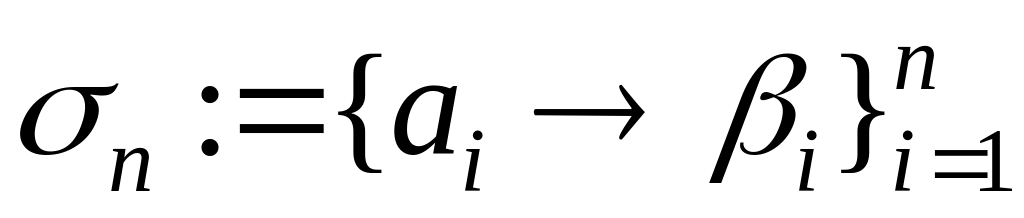 оптимальна для Pn.
Тогда по предшествуюещй лемме
оптимальна для Pn.
Тогда по предшествуюещй лемме
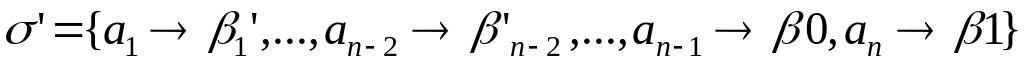 .
Положим
.
Положим
 и рассмотрим схему
и рассмотрим схему
 ,
где j определено так,
чтобы
,
где j определено так,
чтобы
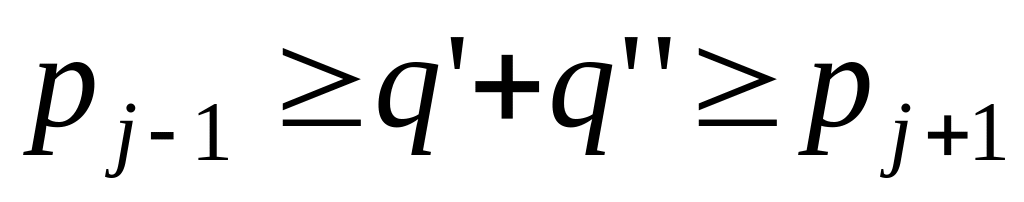 .
.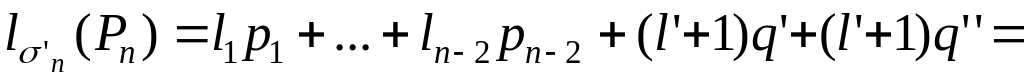
![]()
![]()
5.
![]() - префиксное, значит
- префиксное, значит
![]() тоже префиксное.
тоже префиксное.
6.
![]() - оптимально, значит,
- оптимально, значит,
![]() .
.
7.
![]() ,
но
- оптимально, значит
оптимально.
,
но
- оптимально, значит
оптимально.
