6.3. Помехоустойчивое кодирование

Надежность электронных устройств по мере их совершенствования все время возрастает, но, тем не менее, в их работе возможны ошибки, как систематические, так и случайные. Сигнал в канале связи может быть искажен помехой, поверхность магнитного носителя может быть повреждена, в разъеме может быть потерян контакт. Ошибки аппаратуры ведут к искажению или потере передаваемых или хранимых данных. При определенных условиях, некоторые из которых рассматриваются в этом разделе, можно применять методы кодирования, позволяющие правильно декодировать исходное сообщение, несмотря на ошибки в данных кода. В качестве исследуемой модели достаточно рассмотреть канал связи с помехами, потому что к этому случаю легко сводятся остальные. Например, запись на диск можно рассматривать как передачу данных в канал, а чтение с диска – как прием данных из канала.

6.3.1. Кодирование с исправлением ошибок

Пусть имеется канал связи С, содержащий источник помех:

,

где S – множество переданных, а S’ – соответствующее множество принятых по каналу сообщений. Кодирование F, обладающее таким свойством, что

Называется помехоустойчивым, или самокорректирующимся, или кодированием с исправлением ошибок.

Без ограничения общности можно считать, что A=B={0,1}, и что содержательное кодирование выполняется на устройстве, свободном от помех.

6.3.2. Классификация ошибок

Ошибка в канале могут быть следующих типов:

• - ошибка Тима замещения разряда;

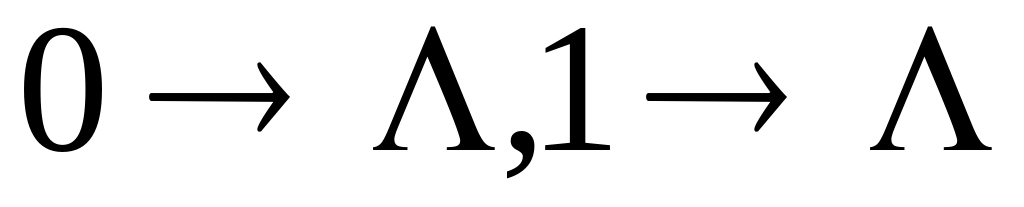• - ошибка типа выпадения разряда;

• - ошибка типа вставки разряда.

Канал характеризуется верхними оценками количества ошибок каждого типа, которые возможны при передаче через канал сообщения определенной длины. Общая характеристика ошибок канала (то есть их количество и типы) обозначается

Пример

Допустим, что имеется канал с характеристикой , то есть в канале возможна одна ошибка типа замещения разряда при передаче сообщения длины n. Рассмотрим следующее кодирование: F(a):=aaa (то есть каждый разряд в сообщении утраивается) и декодирование F^-1(abc):=a+b+c>1 (то есть разряд восстанавливается методом «голосования»). Это кодирование кажется помехоустойчивым для данного канала, однако на самом деле это не так. Дело в том, что при передаче сообщения длины 3n возможно не более 3 ошибок типа замещения разряда, но места этих ошибок совершенно не обязательно распределены равномерно по всему сообщению. Ошибки замещения могут произойти в соседних разрядах, и метод голосования восстановит разряд неверно.

6.3.3. Возможность исправления всех ошибок

Пусть - множество слов, которые могут быть получены из слова s в результате всех возможных комбинаций допустимых в канале ошибок , то есть . Если , то та конкретная последовательность ошибок, которая позволяет получить из слова s слово s’, обозначается . Если тип возможных ошибок в канале подразумевается, то индекс не указывается.

ТЕОРЕМА чтобы существовало помехоустойчивое кодирование с исправлением всех ошибок, необходимо и достаточно, чтобы , то есть неошходимо и достаточно, чтобы существовало разбиение множества B^* на множества B_s ( ), такое что .

Доказательство

Если кодирование помехоустойчивое, то очевидно, что . Обратно: по разбиению , строится функция .

Пример

Рассмотрим канал, в котором в любом передаваемом разряде происходит ошибка типа замещения с вероятностью P (0<p<1/2), причем замещения различных разрядов статистически независимы. Такой канал называется двоичным симметричным. В этом случае любое слово может быть преобразовано в любое другое слово замещениями разрядов. Таким образом, , и исправить все ошибки в двоичном симметричном канале невозможно.