
- •Назовите основные способы реализации искусственных интеллектуальных систем.
- •Приведите структуру доказательств на основе резолюции
- •Назовите основные сферы приложения искусственного интеллекта и охарактеризуйте их.Извлечение информации из баз данных
- •Комбинаторные задачи и составление расписаний
- •Доказательство теорем
- •Автоматическое программирование
- •Роботика
- •Экспертные консультирующие системы
- •Обработка естественного языка
- •2. Дайте определение понятию общеинтеллектуальная процедура (метапроцедура). Опишите процедуру целенаправленного поиска в лабиринте возможностей.
- •1. Дайте определения понятиям "знание" и "данные" и укажите их различие. Назовите основные признаки знаний и дайте им определения.
- •Приведите основные этапы процесса извлечения ответа.
- •Опишите синтаксис и семантику языка предикатов.
- •Опишите процедуру поиска методом редукции.
- •1. Дайте определение понятию "искусственный интеллект". Охарактеризуйте основные теоретические проблемы искусственного интеллекта.
- •2.Охарактеризуйте понятие резолюции в общем виде.
- •Другими словами, помня, что
- •Дайте определения понятиям "знание" и "данные" и укажите их различие.Назовите основные признаки знаний и дайте им определения.
- •Опишите структуру продукционного правила.
- •Перечислите основные виды знаний и охарактеризуйте их.
- •2. Что такое логический вывод? в чем заключается метод решения задач, использующий аппарат логики предикатов
- •1. Что такое предикатная функция?
- •2. Опишите процедуру поиска в глубину. Опишите процедуру поиска в ширину.
- •1. Дайте определение семантической сети.
- •Что такое унификация?
- •1. Перечислите семантические отношения и дайте им определения.
- •2. В чем заключается задача представления некоторой системы в виде системы продукций?
- •1. Перечислите основные типы объектов в семантической сети и дайте им определения.Приведите пример семантической сети.
- •2. Как вычисляются коэффициенты определенности посылок и заключений?
- •Если (а1 а2), то в.
- •В нашем случае
- •Перемножив все компоненты этой формулы, мы увидим, что
- •Дайте определение фрейму
- •Опишите стратегию управления на основе принципа “классной доски”.
- •1. Дайте определение продукционному правилу.
- •2. Как представляется система доказательств в системе опровержения на основе резолюции?
- •1. Назовите группы и типы фреймов. Приведите пример фрейма.
- •2. Опишите стратегию “подъема на гору”.
- •1.Опишите структуру ядра продукционного правила.
- •2.Опишите правило исключения кванторов существования и дайте определение функции Сколема.
- •Опишите основные компоненты системы продукций и связь между ними.
- •2. Опишите процедуру поиска в факторизованном пространстве.
- •1. Что такое интерпретация формулы, область интерпретации?Приведите примеры правильно построенных формул.
- •Приведите последовательность основных этапов тождественных преобразований исходной формулы во множество клауз.
- •1. Что такое продукции?
- •2. Что представляет собой дерево опровержения?
- •1. Что такое стратегия управления в системе продукций?
- •2. Назовите основные стратегии поиска на дереве опровержения.
- •1. Назовите основные признаки и функциональные возможности в соответствии с которыми систему можно отнести к интеллектуальной
- •2. Как применяются методы доказательства теорем к решению задач.
- •1. Опишите процедуру поиска метода генерация – проверка.
- •2. В чем сущность процесса извлечения ответа?
- •1. Опишите методику выработки заключения на основе вероятностных характеристик.
- •2. Опишите используемые в системах продукций стратегии управления.
- •Опишите структуру вывода заключения на основе байесовского подхода.
- •2. Опишите процедуру поиска с использованием нескольких моделей
- •1. Опишите основные принципы дедукции на основе байесовского подхода.
- •2. В чем, на современном этапе исследований, отличие искусственного интеллекта от естественного?Чем отличаются формализованные знания от неформализованных?
- •1. Нечеткие и приближенные высказывания? Что такое коэффициент определенности?
- •Если (а1 а2), то в.
- •2. Приведите структуру доказательств на основе резолюции.
- •Другими словами, помня, что
- •1 Учет нескольких признаков при расчете вероятности гипотезы? Для чего и как рассчитывается цена свидетельств? Как учитывается неопределенность в ответе пользователя?
- •2. Интерпретация формулы, область интерпретации, примеры правильно построенных формул.
2. Как представляется система доказательств в системе опровержения на основе резолюции?
В типичной задаче на доказательство теорем имеем множество Фо формул, исходя из которого нам нужно доказать некоторую формулу F. Системы, основанные на резолюции, предназначены для создания доказательства путем построения противоречия или опровержения. При таком опровержении сначала берется отрицание целевой формулы F и добавляется к множеству Фо. Это расширенное множество затем преобразуется в множество предложений, после чего резолюция используется при попытке вывести противоречие, представляемое пустым предложением NIL.
Предположим, что
некоторая F
логически следует из Фо.
Тогда по определению каждая интерпретация,
удовлетворяющая Фо,
также удовлетворяет и F.
Никакая
интерпретация, удовлетворяющая Фо,
не может удовлетворять
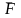 и, следовательно, никакая интерпретация
не может удовлетворять объединению Фо
и
.
Множество формул, которое не может
удовлетворяться ни при какой интерпретации,
называется неудовлетворимым. Таким
образом, если F
следует из Фо,
то множество
и, следовательно, никакая интерпретация
не может удовлетворять объединению Фо
и
.
Множество формул, которое не может
удовлетворяться ни при какой интерпретации,
называется неудовлетворимым. Таким
образом, если F
следует из Фо,
то множество
 является неудовлетворимым.
является неудовлетворимым.
Если резолюция многократно применяется к некоторому неудовлетворимому множеству предложений, то в конце концов будет построено пустое предложение NILL.
Рассмотрим простой пример такого процесса. Пусть предметная область – это множество прямых на плоскости. Предположим, высказаны следующие утверждения:
Прямая А пересекает прямую В
 .
.Прямая В параллельна прямой С
 .
.Если прямые параллельны, то они не пересекаются
 .
.
Если прямые не пересекаются, то они параллельны
 .
.
Если прямая х параллельна прямой у, то прямая у параллельна прямой х
 .
.
Если прямая х параллельна прямой у, а прямая у параллельная прямой z, то прямая х параллельна прямой z
 .
.
Из них необходимо доказать следующее утверждение.
Прямые А и С пересекаются
 .
.
Множество предложений, соответствующих утверждениям с первого по шестое, объединенным с отрицанием седьмого утверждения, имеют вид:
.
.
 .
. .
. .
. .
. .
.
Чтобы доказать нашу теорему опровержением с помощью резолюции, необходимо построить резольвенты для множества предложений 1 – 7, добавить эти резольвенты к множеству и продолжать таким образом, пока не будет получено пустое предложение. Одно из возможных доказательств (их имеется более одного) создает следующую последовательность резольвент:
 резольвента 7 и 4
с использованием подстановки
резольвента 7 и 4
с использованием подстановки
 .
.
 резольвента 2 и 5
с использованием подстановки
резольвента 2 и 5
с использованием подстановки
 .
.
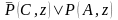 резольвента 6 и 8
с использованием подстановки
резольвента 6 и 8
с использованием подстановки
 .
.
11.
 резольвента 9 и 10 с использованием
подстановки
резольвента 9 и 10 с использованием
подстановки
 .
.
12.
 резольвента 3 и 11 с использованием
подстановки
.
резольвента 3 и 11 с использованием
подстановки
.
13. NILL ( резольвента 1 и 12.
Систему опровержения на основе резолюции можно представить как систему продукций. Глобальной базой данных является множество предложений, а продукционные правила – резолюции. Правила продукции применяются к парам предложений из базы данных при создании некоторой резольвенты выведенного предложения. Тогда новой базой данных становится прежнее множество предложений плюс выведенная резольвента. Условием конца работы для этой системы продукций является результат проверки – содержит ли база данных пустое предложение.
Доказательство с помощью резолюции наглядно можно проиллюстрировать, используя граф, называемый графом опровержения. Вообще, опровержением называется доказательство невыполнимости произвольного множества предложений.
При построении графа опровержения, представляющего собой дерево, предложения из Ф записываются на концевых вершинах графа. Если два предложения, находящихся на каких-либо вершинах, разрешаются, т. е. они имеют резольвенту, то их резольвента записывается на вершине, идущей непосредственно за этими вершинами, которая соединяется с ними ребрами. Корнем дерева опровержения служит пустое предложение, обозначаемое английским словом NILL (NIL – ничего, нуль). Дерево опровержения в отличие от ранее рассмотренных деревьев строится, начиная с концевых вершин, а не с корня.
Стратегия управления направляет поиск опровержения, наращивая граф вывода до тех пор, пока не будет создано дерево, корневая вершина которого помечена пустым предложением NIL.
Билет №14
