Билет 1

1. Назовите основные способы реализации искусственных интеллектуальных систем.

В настоящее время системы ИИ подразделяются на следующие:

• интеллектуальные информационно-поисковые системы (вопросо-ответные системы), обеспечивающие в процессе диалога взаимодействия конечных пользователей – непрограммистов с базами данных и знаний на профессиональных языках пользователей, близких к естественному;

• расчётно-логические системы, позволяющие конечным пользователям, не являющимся программистами в области прикладной математики, решать в диалоговом режиме свои задачи на ЭВМ с использованием сложных математических методов и соответствующих прикладных программ;

• экспертные системы, дающие возможность осуществить эффективную компьютеризацию  областей, в которых знания могут быть представлены в экспертной описательной форме.

Все упомянутые системы ИИ ориентированы на знания, поэтому дальнейший прогресс систем ИИ и новой информационной технологии предопределяет развитие трёх основных теоретических проблем:

• представление знаний – центральная проблема ИИ

• компьютерной лингвистики, решение которой обеспечивает процесс естественно-языкового общения с ЭВМ и прогресс автоматического перевода с иностранных языков;

• компьютерной логики, имеющей особо важное значение для развития экспертных систем, поскольку её цель – моделирование человеческих рассуждений и преобразование программирования из искусства в науку.

2. Приведите структуру доказательств на основе резолюции

Рассмотрим последовательно тождественные преобразования, которые необходимо выполнить в процессе преобразования формулы в предложения.

1. Исключение знаков импликации. Знак импликации можно исключить, используя равенство (А  В) = ( ).

Например:

;

.

2. Уменьшение области действия знаков отрицания. Уменьшить область действия знаков отрицания, т. е. сделать так, чтобы символ отрицания применялся не более, чем к одному литералу, можно используя равенства

.

Используя эти равенства, например, получаем

.

3. Стандартизация переменных. В области действия кванторов связанную с ними переменную можно заменить произвольной переменной, не совпадающей с какой-либо другой переменной, входящей в область действия этих кванторов. Например,

.

4. Исключение кванторов существования. В формуле , которую можно интерпретировать, например, как «для всех x существует такой y, что x не больше y», квантор находится внутри области действия квантора 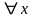. Поэтому y который «существует», зависит от x. Положим, что эта зависимость в явном виде определяется с помощью функции g(x), отображающей каждое значение x в y. Такая функция называется функцией Сколема. Используя ее, можно исключить квантор существования. Для обозначения функции Сколема не должны использоваться функциональные буквы, которые уже имеются в формуле. Если квантор существования находится в области двух или более кванторов общности, то функция Сколема будет зависеть соответственно от двух аргументов и более.

Если исключаемый квантор существования не принадлежит области действия ни одного квантора общности, то функция Сколема не содержит аргумента, т. е. является константой. Так, формула при исключении квантора существования преобразуется в формулу F(A), где A – константа, про которую известно, что она «существует».

Пример: Выражение после введения функции Сколема и удаления квантора существования имеют вид:

.

5. Так как с каждым квантором связана своя переменная (пункт 3), то порядок расположения кванторов общности не имеет значения, поэтому эти кванторы можно явно не указывать, т. е. исключить, условившись, что все переменные в формулах относятся к кванторам общности.

6. Представление формулы к конъюнктивно-нормальной форме. Любую формулу, полученную после проведения преобразований 1 – 5, можно привести к конъюнктивно-нормальной форме многократным применением дистрибутивных правил, а именно: заменой выражений вида на . При этом формула будет представлена как конъюнкция конечного множества дизъюнкций литералов. Говорят, что такая формула находится в нормальной конъюнктивной форме.

7. Исключение символов . Так как какая-либо интерпретация удовлетворяет формуле вида в том и только в том случае, когда она удовлетворяет формулам k₁, k₂, … , k_n одновременно, то исходную формулу в Ф₁ можно заменить множеством конъюнктивных членов (предложений).

Рассмотрим пример преобразования формулы в предложения. Пусть задана формула

.

Исключим знаки импликации:

.

Уменьшим области действия знаков отрицания до одного предиката:

.

Произведем стандартизацию переменных:

.

Исключим все кванторы:

.

Здесь g(x) – функция Сколема.

Квантор существования z находится в области действия только одного квантора общности x, и поэтому функция Сколема зависит только от x. Используя свойство (закон) дистрибутивности дизъюнкции относительно конъюнкции, последняя формула легко приводится к КНФ, откуда получаются следующие предложения:

.

Билет №2