§5. Принцип относительности Галилея.

Допустим, что нами выбрана некоторая ИСО. После того как этот выбор сделан, можно указать бесконечное множество твердых тел, движущихся относительно выбранной ИСО равномерно и поступательно. Принимая указанные тела за тела отсчета, мы получим тем самым бесконечное множество других ИСО.

Если теперь рассмотреть механическое движение некоторой замкнутой системы с точки зрения всех ИСО, то легко убедится, что: 1) механическое движение относительно (т.е. положения, скорости и вид траекторий материальных точек зависят от выбора той или иной ИСО); 2) в то же время законы механики (законы Ньютона) одинаковы во всех ИСО. Относительность механического движения и одинаковость законов механики в разных ИСО и составляют содержание принципа относительности Галилея (ПОГ): все ИСО в механике равноправны (физически равноценны) в том смысле, что законы механики во всех таких ИСО имеют одинаковую форму.

Математически ПОГ выражает инвариантность уравнений (законов) механики по отношению к преобразованию координат и времени при переходе от одной ИСО к другой (преобразования Галилея).

При получении преобразований Галилея существенно используются однородность и изотропность пространства и однородность и абсолютность времени (см. § 2).

Р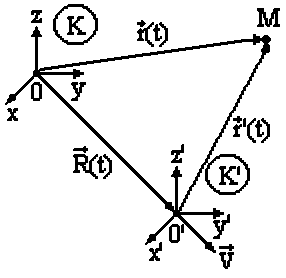 ассмотрим материальную точку М в двух произвольных ИСО и , движущихся друг относительно друга с постоянной скоростью 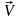(см. рисунок). Если начало координат 0 и 0' в начальный момент t=0 совпадают, то 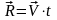. Из рисунка видно, что

,

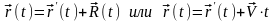поэтому с учетом абсолютности времени получаем преобразования Галилея:

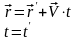(5.1)

Преобразованию Галилея соответствует следующий закон сложения скоростей:

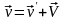. (5.2)

Дифференцируя (5.2), получаем связь между ускорениями материальной точки в обеих ИСО:

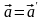(5.3)

Инвариантность (неизменность) ускорение (5.3) с учетом инвариантности силы и массы приводит к инвариантности законов Ньютона при преобразованиях (5.1), что и является математическим выражением ПОГ.

Замечание. То обстоятельство, что преобразования Галилея (5.1) невозможно получить без учета однородности и изотропности пространства и однородности времени, физически означает, что ПОГ автоматически содержит (выражает) также и инвариантность законов механики к трем типам преобразований: 1) переносу в пространстве; 2) обращению в пространстве; 3) сдвигу во времени. Эти последние инвариантности (симметрии) законов механики связанный с законами сохранения энергии, импульса и момента импульса (см. главу 2).

§ 6. Основная задача динамики и роль начальных условий. Принцип причинности классической механики.

Рассмотрим движение относительно ИСО некоторой механической системы, состоящей из n материальных точек с постоянными массами m₁, m₂, … , m_n. Если обозначить через 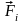равнодействующую (результирующую) всех сил, действующую на i-ю точку, то применение к этой системе второго закона Ньютона (4.3) позволяет записать ее уравнения движения в виде

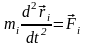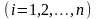, . (6.1)

Если рассмотренная система не замкнута, то каждую можно записать в виде

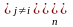, (6.2)

где 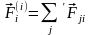- равнодействующая всех внутренних сил 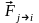со стороны других (j ≠ і) точек системы; - равнодействующая всех

внешних сил, которые действуют на i-ю точку системы со стороны тел, не входящих в эту систему. Таким образом, дифференциальные уравнения движения механической системы можно окончательно записать в виде

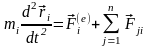(6.1’)

В (6.1’) предполагается, что внутренние силы 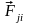удовлетворяют третьему закону Ньютона (4.5). Относительно внешних сил будем предполагать, что они в общем случае могут явно зависеть от времени t, а так же от положения и скоростей соответствующих точек системы относительно внешних тел.

Основная задача динамики состоит в отыскании радиусов-векторов материальных точек как функций времени 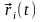и их скоростей 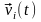по заданным внутренним и внешним силам и известным массам частиц m_i. В математическом отношении эта задача сводится к нахождению общего решения системы обыкновенных дифференциальных уравнений второго порядка (6.1’).

Замечание. Для дальнейшего существенно, что далеко не всегда внешние силы могут быть заданы (известны) до решения основной динамической задачи. Дело в том, что в большинстве задач механики приходится изучать движение так называемых несвободных систем, т.е. систем, перемещения которых ограниченны связями. Эффект действия связей в уравнениях (6.1’) учитывается с помощью таких внешних сил, которые называются реакциями связей и величины, которых заранее неизвестны, что существенно усложняет решение уравнений движения. Поэтому сам характер постановки основной задачи динамики здесь (заданность всех ) исключает пока рассмотрение несвободных механических систем, т.е. дальнейшие выводы справедливые фактически только для так называемых свободных систем. Будем называть механическую систему свободной, если под действием приложенных сил материальные точки могут занимать любые положения в пространстве – для таких систем в любой момент времени t можно произвольным образом задать значения 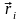и 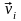всех ее точек.

Общий ход решения основной задачи динамики сводится к следующему. Находим общее решение системы уравнений (6.1’), которое (если оно вообще существует) можно представить в виде

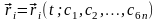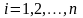, . (6.3)

Дифференцируя (6.3) по t можно получить скорости 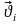материальных точек как функции времени

, . (6.4)

Общие решения (6.3) и (6.4) содержат 6n произвольных постоянных с₁, с₂,…,с_6n (так как (6.1’) в любой системе координат есть система 3n дифференциальных уравнений 2^го порядка), поэтому дальнейшая конкретизация этих решений связанна с определением этих постоянных как некоторых физических характеристик системы. Покажем, что c₁, c₂,…,c_6nможно выразить через так названные начальные координаты 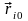и скорости 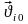точек системы в момент времени t=0, воспользовавшись начальными условиями следующего вида:

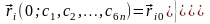, . (6.5)

Действительно, (6.5) есть система 6n алгебраических уравнений относительно 6n постоянных c₁, c₂, …, c_6n , поэтому единственное решение (6.5) можно записать в виде

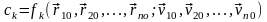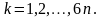, . (6.6)

Наконец, подстановка (6.6) в (6.3) и (6.4) позволяет получить окончательное решение основной динамической задачи:

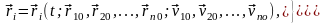, . (6.7)

Из обсуждения общего хода решения основной задачи динамики можно сделать следующие важные выводы:

1. Состояние (свободной) механической системы в любой момент времени t полностью определяется заданием и всех материальных точек системы в тот же момент времени t.

Это означает, что в этот же момент времени t однозначно определяются и ускорения 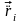материальных точек, знание которых необходимо для предсказания поведения системы в последующие моменты времени. Однако, в отличие от и ускорение нельзя задавать произвольно, так как они определяются уравнениями движения (6.1’).

Отметим, что возможность определения состояния механической системы с помощью ее координат и скоростей (или импульсов) базируется на допущении классической механикой возможности одновременного измерения положение 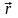и скорости 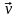материальной точки и, следовательно, любых механических характеристик системы (которые являются функциями координат и скоростей). Это означает, что взаимодействием измерительного прибора с механической системой всегда можно пренебречь в силу его малости. Поэтому считается, что процесс измерения любой физической величины не изменяет состояния движения системы и, следовательно, не изменяет самой измеряемой величины (например, измерение положения материальной точки не сказывается на ее координатах). Хотя указанное допущение с большой точностью выполняется для макроскопических систем, однако для микрообъектов оно несправедливо (например, у микрочастиц нельзя одновременно точно измерить координату x и импульс p_х). Поэтому для микросистем указанный выше способ определения состояния обнаруживается полностью непригодным.

2. Заданием начального состояния механической системы однозначно определяется ее поведение и во все последующие моменты времени.

Это означает, что если заданы условия движения системы, т.е. заданы силы , то по начальному состоянию системы в момент времени t=0 можно однозначно предсказать ее состояния и во все последующие моменты времени t>0.

Сформулированное утверждение представляет собой принцип причинности классической механики, так ли называемый принцип Лапласовского детерминизма. Это есть частная формулировка (справедливая только в рамках МКМ) общего принципа причинности – одного из важнейших методологических принципов физики.