
- •Введение.
- •Логическая структура современной физики.
- •Границы применимости физической теории.
- •Глава 1. Основные понятия и законы классической механики.
- •§2. Классические представления о пространстве и времени и их арифметизация.
- •§3. Кинематические и динамические характеристики механического движения.
- •§4. Законы динамики Ньютона.
- •§5. Принцип относительности Галилея.
- •§ 6. Основная задача динамики и роль начальных условий. Принцип причинности классической механики.
- •§ 7. Потенциальная энергия и классификация свободных механических систем.
- •Глава. 2. Законы сохранения и принцип симметрии.
- •§ 8. Первые интегралы уравнений движения и законы сохранения.
- •§ 9. Закон сохранения энергии и его связь с однородностью времени.
- •§ 10. Закон сохранения импульса и его связь с однородностью пространства.
- •§ 11. Закон сохранения момента импульса и его связь с изотропностью пространства.
- •Глава 3. Основы аналитической механики.
- •§ 12. Постановка задачи о движении несвободной механической системы. Классификация связей.
- •13. Уравнения Лагранжа. Функция Лагранжа.
- •С учетом (13.12) перепишем уравнения (13.11) в окончательном виде
- •§ 14. Функция Лагранжа и законы сохранения.
- •§ 15. Основная задача вариационного исчисления. Уравнения Эйлера.
- •Простейшим функционалом является криволинейный интеграл
- •Интегрируя второй интеграл в правой части (15.6) по частям с учетом предельных условий (15.4) получаем:
- •Обобщим полученные результаты для функционала
- •§ 16. Принципы наименьшего действия Гамильтона-Остроградського.
- •§ 17. Канонические уравнения движения.
- •Подставляя (17.8) в (17.7), получаем
- •§ 18. Скобоки Пуассона.
- •§ 19. Уравнение Гамильтона-Якоби.
§ 16. Принципы наименьшего действия Гамильтона-Остроградського.
Математические методы, развитые в § 15, позволяют получить новую формулировку классической механики, когда в качестве основной ее аксиомы принимается некоторый интегральный вариационный принцип – принцип наименьшего действия. Этот принцип связан с изучением экстремальных свойств некоторой интегральной характеристики движения механической системы, являющейся в математическом плане функционалом типа (15.10).
На
справедливость сделанного утверждения
нас наталкивают следующие формальные
соображения. Если в уравнениях Эйлера
(15.20) произвести формальные замены:
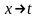 ,
,
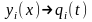 ,
и
,
и
 ,
то уравнения (15.20) совпадут с уравнениями
Лагранжа в форме (13.18). Это означает, что
уравнения Лагранжа (13.18), которые являются
дифференциальными уравнениями движения
голономных
механических систем с идеальными связями
и потенциальными
(или обобщенно-потенциальными)
активными силами, можно рассматривать
как уравнения Эйлера по отношению к
основной вариационной задаче для
некоторого функционала S типа (15.10),
имеющего с учетом указанных формальных
замен вид
,
то уравнения (15.20) совпадут с уравнениями
Лагранжа в форме (13.18). Это означает, что
уравнения Лагранжа (13.18), которые являются
дифференциальными уравнениями движения
голономных
механических систем с идеальными связями
и потенциальными
(или обобщенно-потенциальными)
активными силами, можно рассматривать
как уравнения Эйлера по отношению к
основной вариационной задаче для
некоторого функционала S типа (15.10),
имеющего с учетом указанных формальных
замен вид
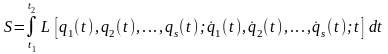 .
(16.1)
.
(16.1)
Т.о.,
результаты § 15 позволяют утверждать:
уравнения
Лагранжа (13, 18) равносильны требованию
обращения в нуль вариации
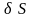 функционала
(16, 1):
функционала
(16, 1):
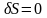 .
(16.2)
.
(16.2)
Для
того, чтобы раскрыть физическое
содержание вариационного уравнения
(16,2), т.е. возвести его в статус физического
принципа,
необходимо осмыслить физическую
постановку задачи, приводящую к
необходимости
и достаточности
требования (16,2), а также придать физический
смысл функционалу
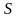 .
С этой целью удобно воспользоваться
понятием расширенного
конфигурационного пространства
механической системы, которым называется
абстрактное пространство обобщенных
координат
.
С этой целью удобно воспользоваться
понятием расширенного
конфигурационного пространства
механической системы, которым называется
абстрактное пространство обобщенных
координат
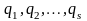 и времени
размерности
и времени
размерности
 ,
где
- число степеней свободы системы (просто
конфигурационным
пространством называется пространство
измерений
,
где
- число степеней свободы системы (просто
конфигурационным
пространством называется пространство
измерений
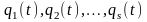 – см. напр., Голдстейна).
– см. напр., Голдстейна).
Так
как каждый набор координат
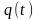 задает пространственное положение
системы в момент времени
задает пространственное положение
системы в момент времени
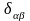 (т.е. конфигурацию
системы), то каждой точке рассмотренного
конфигурационного пространства с
координатами
(т.е. конфигурацию
системы), то каждой точке рассмотренного
конфигурационного пространства с
координатами
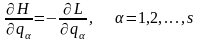 однозначно
соответствует определенная конфигурация
системы в момент
однозначно
соответствует определенная конфигурация
системы в момент
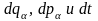 .
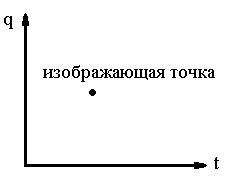
Для наглядности условимся использовать
следующее геометрическое изображение
рассмотренного конфигурационного
пространства на плоскости: по оси абсцисс
будем откладывать время
,
а по оси ординат – совокупность значений
всех
обобщенных координат
;
тогда имеем соответствие: точки на
плоскости
соответствует определенная конфигурация
системы в момент
.
.
Для наглядности условимся использовать
следующее геометрическое изображение
рассмотренного конфигурационного
пространства на плоскости: по оси абсцисс
будем откладывать время
,
а по оси ординат – совокупность значений
всех
обобщенных координат
;
тогда имеем соответствие: точки на
плоскости
соответствует определенная конфигурация
системы в момент
.
Теперь поставим следующую физическую задачу.
П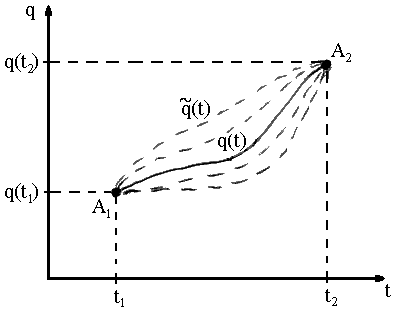 усть
за небольшой
(но конечный) промежуток времени
усть
за небольшой
(но конечный) промежуток времени
 связанная система переходит в результате
своего движения из некоторой заданной
конфигурации
связанная система переходит в результате
своего движения из некоторой заданной
конфигурации
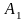 в новую заданную конфигурацию
в новую заданную конфигурацию
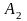 (см. рис. (16.1)).
(см. рис. (16.1)).
Рисунок 16.1
Наложенные
на систему связки
допускают множество различных
кинематически
возможных движений
за одно и то
же время
системы (см. тему (5) § 12, особенно рис.
(12.3)), которые на рис. (16.1) изображены
пунктирными конфигурационными
траекториями
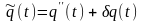 ;
при этом одно из этих движений является
действительным
(сплошная траектория
на рис. (16,1)). Возникает
задача: как
из всех кинематически за одно и то же
время
движений выделить действительное
движение системы, т.е., другими словами,
как найти закон
движения
механической системы, если
;
при этом одно из этих движений является
действительным
(сплошная траектория
на рис. (16,1)). Возникает
задача: как
из всех кинематически за одно и то же
время
движений выделить действительное
движение системы, т.е., другими словами,
как найти закон
движения
механической системы, если
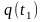 и
и
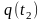 заданы
заданы
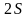 граничными условиями
граничными условиями
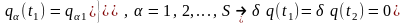 (16.3)
(16.3)
Требование (16.2) и является достаточным условием решения поставленной физической задачи, т.е. из (16.2) автоматически вытекает закон движения системы.
Действительно, для изучаемой системы, как мы показали в начале этого параграфа, из (16.2) автоматически с необходимостью вытекают (в качестве уравнений Эйлера) уравнения Лагранжа (13.18), решения которых и дают закон движения системы.
Докажем теперь необходимость требования (16.2) для действительного движения голономной системы с идеальными связями и обобщенно-потенциальными активными силами, т.е. докажем, что из уравнений Лагранжа (13.18) с необходимостью вытекает условие (16.2). Для этого каждое из уравнений (13.18)
,
с
номером
умножим на
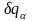 и сложим полученные результаты, что
приводит к уравнению
и сложим полученные результаты, что
приводит к уравнению
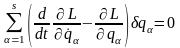 .
(16.4)
.
(16.4)
С помощью очевидного тождества
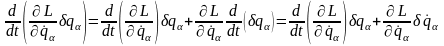
перепишем (16.4) в виде
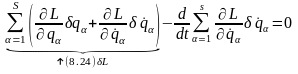
или
с учетом определения вариации функции
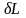 (см. § 15) и
(см. § 15) и
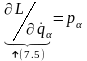 ,
в виде
,
в виде
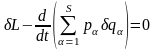 .
(16.4’)
.
(16.4’)
Умножая
(16.4’) на
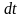 и интегрируя в пределах от
и интегрируя в пределах от
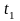 до
до
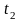 ,
получаем
,
получаем
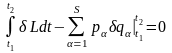 ,
,
откуда,
учитывая, что согласно (16.3)
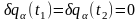 ,
и принимая во внимание перестановочность
операций интегрирования и варьирования
(15.28), мы и приходим к необходимости
условия (16.2).
,
и принимая во внимание перестановочность
операций интегрирования и варьирования
(15.28), мы и приходим к необходимости
условия (16.2).
Изложенное
приводит нас к выводу, что функционал
,
определенный формулой (16.1), является
важнейшей скалярной характеристикой
движения
механической системы, которая называется
функцией
действия
или просто действием
по Гамильтону.
Действие
,
имеющее размерность произведения
энергии на время (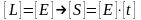 ), обладает следующими общими свойствами:
1)
есть функционал, областью определения
которого является класс кинематически
возможных движений
системы за одно
и то же время;
2)
принимает экстремальное
(минимальное
при достаточно малом времени рассмотрения
движения) значение для действительного
(фактически происходящего) движения
системы.
), обладает следующими общими свойствами:
1)
есть функционал, областью определения
которого является класс кинематически
возможных движений
системы за одно
и то же время;
2)
принимает экстремальное
(минимальное
при достаточно малом времени рассмотрения
движения) значение для действительного
(фактически происходящего) движения
системы.
Теперь
мы можем сформулировать один из важнейших
вариационных принципов классической
механики – принцип
наименьшего действия (ПНД)
Гамильтона-Остроградского
(первая половина ХІХ ст.): среди всех
кинематически возможных движений
механической системы из одной конфигурации
в другую (близкую к первой), совершаемых
за один и тот же промежуток времени,
действительным является то движение,
для которого действие по Гамильтону
будет наименьшим; математическое
выражение ПНД имеет вид
(16.2), где
 - символ неполной (изохронной) вариации
(т.е. в отличие от полной вариации в ней
время не варьируется).
- символ неполной (изохронной) вариации
(т.е. в отличие от полной вариации в ней
время не варьируется).
Хотя выше мы привели доказательство справедливости ПНД в форме Гамильтона-Остроградского только для голономных механических систем с идеальными связями и потенциальными (или обобщенно-потенциальными) активными силами, однако его можно обобщить и на голономные системы с неконсервативными активными силами и даже распространить на неголономные механические системы (см. Ольховский, Жирнов, Голдстейн).
Это фактически означает, что кроме индуктивного метода построения классической механики (когда за основу построения принимаются дифференциальные уравнения Ньютона) существует и дедуктивный метод, когда в качестве основной и единственной аксиомы принимается ПНД Гамильтона-Остроградского, при этом уравнения движения (13.13) выступают как уравнения Эйлера некоторой вариационной задачи.
Замечание
1. Кроме
ПНД в форме Гамильтона-Остроградского
известен также ПНД в
форме Мопертюи-Лагранжа,
в котором используется действие
по Лагранжу
и понятие полной
вариации (когда варьируются не только
и
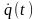 ,
но и время
движения системы из одной конфигурации
в другую). Этот принцип является менее
общим, так как применим только для
консервативных
и при том голономных
систем (см. Ольховский, Голдстейн).
,
но и время
движения системы из одной конфигурации
в другую). Этот принцип является менее
общим, так как применим только для
консервативных
и при том голономных
систем (см. Ольховский, Голдстейн).
Замечание 2. Преимущество вариационной концепции классической механики (по сравнению с индуктивным способом ее построения) заключается прежде всего в следующем. Во-первых, ПНД (16.2) инвариантен относительно любого точечного преобразования обобщенных координат (13.14), в том числе и относительно точечного преобразования, связанного с переходом от инерциальной системы отсчета к любой неинерциальной системе отсчета, т.е. вариационная концепция не зависит от выбора системы отсчета. Во-вторых, ПНД (16.2) нетрудно распространить на системы, имеющие бесконечно большое число степеней свободы, т.е. на системы, не являющиеся механическими (например, на электромагнитные поля и поля элементарных частиц); другими словами, во всех известных ФКМ при построении физических теорий можно сформулировать вариационные принципы, аналогичные принципу (16.2) и позволяющие получать соответствующие им «уравнения движения» (например, уравнения Максвелла в классической электродинамике, уравнение Шредингера в квантовой механике и т.д.). Возможность формулировки ПНД в различных областях физики свидетельствует о единстве физической реальности и общности форм проявления различных физических процессов.
Замечание 3. Из ПДН (16.2) вытекает важное следствие: функция Лагранжа механической системы определена лишь с точностью до полной производной по временем от произвольной функции обобщенных координат (но не скоростей!) и времени, т.е. (16.2) и, следовательно, уравнения Лагранжа (13.18) инварианты относительно преобразования
 .
(16.5)
.
(16.5)
Действительно,
действия
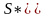 и
,
определяемы функциями Лагранжа
и
,
определяемы функциями Лагранжа
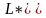 и
по формуле (16.1), связанны соотношением
и
по формуле (16.1), связанны соотношением
 ,
,
откуда
видно, что условие
совпадает с условием
 ,
что и требовалось доказать. Правилом
(16.5) часто пользуются для выбора самой
простой и удобной
.
,
что и требовалось доказать. Правилом
(16.5) часто пользуются для выбора самой
простой и удобной
.
Замечание
4. Т.к. для
уравнений движения существенна не самая
вариация
 ,
а только факт его равенства нулю,
,
то умножение
на произвольную константу также не
изменит уравнений движения. Поэтому,
казалось бы, что можно считать, что
определяется
также и с точностью до мультипликативной
постоянной.
Этому, однако, препятствует одно
физическое
соображение, которое можно назвать
условием асимптотической
аддитивности:
если некоторая механическая система
(І+ІІ) разделяется на две подсистемы І
и ІІ так, что минимум расстояния между
материальными точками разных подсистем
,
а только факт его равенства нулю,
,
то умножение
на произвольную константу также не
изменит уравнений движения. Поэтому,
казалось бы, что можно считать, что
определяется
также и с точностью до мультипликативной
постоянной.
Этому, однако, препятствует одно
физическое
соображение, которое можно назвать
условием асимптотической
аддитивности:
если некоторая механическая система
(І+ІІ) разделяется на две подсистемы І
и ІІ так, что минимум расстояния между
материальными точками разных подсистем
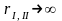 ,
то физически
очевидно, что
,
то физически
очевидно, что
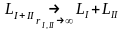 .
(16.6)
.
(16.6)
Поэтому
при умножении
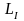 и
и
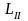 на разные
(произвольные) множители равенство
(16.6) разрушилось бы, что недопустимо.
Т.о., остается только возможность умножать
одновременно
все
функции
на одну и ту же константу – но такая
операция по существу сводится к изменению
системы единиц. Поэтому свободы умножения
на произвольную
константу нет.
на разные
(произвольные) множители равенство
(16.6) разрушилось бы, что недопустимо.
Т.о., остается только возможность умножать
одновременно
все
функции
на одну и ту же константу – но такая
операция по существу сводится к изменению
системы единиц. Поэтому свободы умножения
на произвольную
константу нет.
Замечание
5. Ядро
,
т.е.
содержит только от обобщенных скоростей
(а не
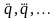 ),
вследствие чего уравнения движения
(Лагранжа-Эйлера) есть уравнения 2го
порядка, т.е. их решения (частные)
однозначно определяются заданием
состояния системы
),
вследствие чего уравнения движения
(Лагранжа-Эйлера) есть уравнения 2го
порядка, т.е. их решения (частные)
однозначно определяются заданием
состояния системы
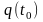 и
и
 в момент
в момент
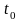 .
.
На
самом деле аргументация развивается в
противоположном
направлении: мы поэтому и допустим в
только
(но не
)
чтобы состояние системы определялось
и
.
Можно развивать теории
с высшими производными
, для которых в
входят и
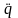 ,
и
,
и
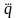 и т.д. (Рассмотрение этих теорий полезно
в некоторых специальных разделах физики
(например, в некоторых направлениях
развития теории физических полей).
и т.д. (Рассмотрение этих теорий полезно
в некоторых специальных разделах физики
(например, в некоторых направлениях
развития теории физических полей).
Замечание
6. Если
характерные для физической задачи
величины размерности
действия
сравнимы по величине с квантом
действия
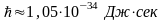 (постоянной
Планка), то
рассмотрение движения физической
системы следует вести на основе более
общей механики – квантовой
механики
(см. часть IV).
(постоянной
Планка), то
рассмотрение движения физической
системы следует вести на основе более
общей механики – квантовой
механики
(см. часть IV).
