Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»
Институт информационных систем управления
Кафедра прикладной математики
РАБОТА №2
По дисциплине
«Математическая статистика»
Тема работы :
«Дисперсионный анализ»
Выполнил: студент группы ПМиИ2-1 Вельможина И.Р.
Проверил: Калинина В.Н.
Москва – 2012
РАБОТА 2. Дисперсионный анализ.
i) Однофакторный дисперсионный анализ (выполняется с применением программы «Однофакторный дисперсионный анализ» надстройки «Анализ данных» пакета Microsoft Excel).
Задача. Сведения
о количестве голосов Y,
отданных за кандидата в
трех однотипных
случайно выбранных избирательных
округах, в которых
использовались
разные виды агитации ( — личные встречи кандидата с
избирателями,
— личные встречи кандидата с
избирателями,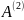 — раздача листовок с программой
кандидата,
— раздача листовок с программой
кандидата,
 —
выступление кандидата по телевидению),
приведены для каждого
варианта в прил.
2, а.
Требуется:
—
выступление кандидата по телевидению),
приведены для каждого
варианта в прил.
2, а.
Требуется:
1. Записать детерминированную модель дисперсионного анализа количества голосов, поданных за кандидата в избирательном округе, и предъявляемые к ней требования. На 5%-ном уровне значимости проверить
гипотезу о равенстве групповых генеральных дисперсий количества голосов, используя критерий Бартлетта.
2. Построить дисперсионную таблицу; на 5%-ном уровне значимости проверить гипотезу об отсутствии влияния видов агитации на количество голосов, поданных за кандидата.
3. В случае, если эта гипотеза отвергается:
а) оценить влияние видов агитации на количество голосов, используя коэффициент детерминации;
б) на 5%-ном уровне значимости провести попарное сравнение влияния видов агитации.
4. Оценить параметры модели.
ii) Двухфакторный дисперсионный анализ (выполняется с применением
программы «Двухфакторный дисперсионный анализ с повторениями» надстройки «Анализ данных» пакета Microsoft Excel).
Задача. При
исследовании зависимости средней оценки
Y по
математической статистике в группе от
метода обучения (
— традиционный классический,
—
компьютерный,
—
комбинированный), будущей специальности
( — «Менеджмент
организации»,
— «Менеджмент
организации»,
 —
«Социология»)
и их взаимодействия
было выделено случайным образом 18 групп,
которые приписывались в равных количествах
шести комбинациям методов и специальностей.
Знания оценивались тестом, состоящим
из 120 вопросов. Сведения о
среднем числе
правильных ответов в группах приведены
для каждого варианта в прил. 2, б.
Требуется:
—
«Социология»)
и их взаимодействия
было выделено случайным образом 18 групп,
которые приписывались в равных количествах
шести комбинациям методов и специальностей.
Знания оценивались тестом, состоящим
из 120 вопросов. Сведения о
среднем числе
правильных ответов в группах приведены
для каждого варианта в прил. 2, б.
Требуется:
1. Записать детерминированную модель двухфакторного дисперсионного анализа (с повторениями) средней оценки по математической статистике в группе и предъявляемые к модели требования; проверить гипотезу о равенстве групповых генеральных дисперсий.
2. Построить дисперсионную таблицу; на 5%-ном уровне значимости проверить гипотезы об отсутствии влияния на среднюю оценку: метода обучения; будущей специальности; взаимодействия метода обучения и будущей специальности.
3. При отклонении каких-либо из перечисленных гипотез рассчитать соответствующий коэффициент детерминации.
4. Оценить параметры модели.
Однофакторный дисперсионный анализ .
Сведения о количестве
голосов Y,
отданных за кандидата в трех однотипных
случайно выбранных избирательных
округах, в которых использовались разные
виды агитации ( —
личные встречи кандидата с избирателями,
—
личные встречи кандидата с избирателями,
 —
раздача листовок с программой кандидата,
—
раздача листовок с программой кандидата,
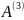 —
выступление кандидата по телевидению),
приведены в табл. 1.
—
выступление кандидата по телевидению),
приведены в табл. 1.
Исходные данные для однофакторного дисперсионного анализа
Вариант №4
-
Номер избирательного участка
1
63
65
79
2
63
68
79
3
64
69
80
4
72
79
88
5
73
87
6
87
Таблица 1
Пункт 1 . Детерминированная модель однофакторного дисперсионного анализа количества голосов ,поданных за кандидата в избирательном округе имеет следующий вид :

К этой модели предъявляются следующе требования :
Все случайные величины


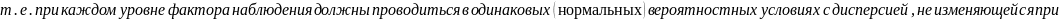
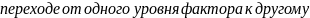 ;
;
В однофакторном дисперсионном
анализе проверяют гипотезу
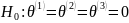 ,
,
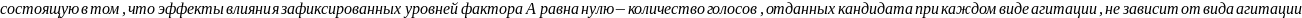 .
.
Рис. 1 Числовые данные для программы « Однофакторный дисперсионный анализ»
|
|
|
63 |
65 |
79 |
63 |
68 |
79 |
64 |
69 |
80 |
72 |
79 |
88 |
73 |
|
87 |
|
|
87 |
Рис.2. Результаты работы программы «Однофакторный дисперсионный анализ»
Однофакторный дисперсионный анализ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ИТОГИ |
|
|
|
|
|
|
Группы |
Счет |
Сумма |
Среднее |
Дисперсия |
|
|
|
5 |
335 |
67 |
25,5 |
|
|
|
4 |
281 |
70,25 |
36,91666667 |
|
|
|
6 |
500 |
83,33333333 |
19,46666667 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
|
|
|
Источник вариации |
SS |
df |
MS |
F |
P-Значение |
F критическое |
Между группами |
821,5166667 |
2 |
410,7583333 |
15,89604945 |
0,000423363 |
3,885293835 |
Внутри групп |
310,0833333 |
12 |
25,84027778 |
|
|
|
|
|
|
|
|
|
|
Итого |
1131,6 |
14 |
|
|
|
|
Проверим на 5%-ном уровне
значимости гипотезу о равенстве групповых
генеральных дисперсий количества
голосов ,предположив нормальность
распределения случайных величин
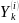 и их независимость . Для этого применим
критерий Барлетта
.
и их независимость . Для этого применим
критерий Барлетта
.
Рассчитано программой :
«Счет» - число наблюдений на каждом уровне
 .
.
«Сумма» - сумма значений для каждого уровня (
 )
.
)
.«Среднее» - несмещенные оценки групповых средних
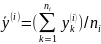 .
.«Дисперсия» -групповые дисперсии для каждого уровня
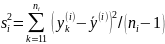 (
(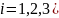 .
.
Для расчета числового значения статистики Барлетта
 ,
где
,
где
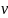 =3
– число уровней фактора ,
=3
– число уровней фактора ,

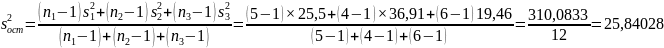
Где числовое значение
статистики Барлетта
 будет равно
будет равно

Статистика Барлета
в предположении справедливости гипотезы
о равенстве групповых генеральных
дисперсий имеет распределение , близкое
к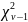 . При
. При
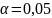 критическая точка
критическая точка
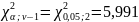 . Поскольку
. Поскольку
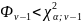 , то есть
, то есть
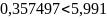 , нет оснований отвергнуть проверяемую
гипотезу .
, нет оснований отвергнуть проверяемую
гипотезу .
Пункт 2 . Таблица
«Дисперсионный анализ» , полученная в
результате работы программы , представляет
собой дисперсионную
таблицу . Расшифруем
ее отдельные ячейки в Табл.2. В этой
таблице
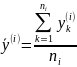 ,
,
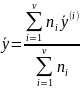 .
.
Источник вариации результативного признака Y |
Показатель вариации
|
Число степеней свободы
( |
Оценка дисперсии
|
|
|
|
Фактор А |
|
|
|
15,89 |
0,000423363 |
3,885293835 |
Остаточные факторы |
|
|
|
|
||
Общая вариация |
|
|
|
|
|
|
Проверка гипотезы
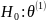 =
= производится на основе анализа статистики
производится на основе анализа статистики
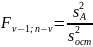 ,
имеющей ( в предположении справедливости
,
имеющей ( в предположении справедливости
 ) распределение Фишера-Снедекора с
и
степенями свободы . Мы отвергаем гипотезу
так как
) распределение Фишера-Снедекора с
и
степенями свободы . Мы отвергаем гипотезу
так как
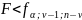 , то есть
, то есть
 , то есть
, то есть
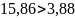 . Гипотезу
можно проверить и так : если Р-значение
не меньше принятого уровня значимости
,гипотезу
принимают , а если Р-значение оказывается
меньше , то
отвергают .В нашем случае
. Гипотезу
можно проверить и так : если Р-значение
не меньше принятого уровня значимости
,гипотезу
принимают , а если Р-значение оказывается
меньше , то
отвергают .В нашем случае
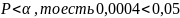 , значит гипотезу
мы отвергаем .
, значит гипотезу
мы отвергаем .
Пункт 3 . а) Таким образом , вид агитации существенно влияет на количество голосов ,отданных за кандидата . Оценим силу этого влияния с помощью коэффициента детерминации
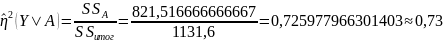 – такова (73%) доля общей
вариации наблюдаемого числа голосов ,
отданных за кандидата , обусловленная
изменчивостью фактора
– такова (73%) доля общей
вариации наблюдаемого числа голосов ,
отданных за кандидата , обусловленная
изменчивостью фактора
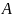 -
вида агитации . Влиянием не контролируемых
факторов обусловлено 27% вариации числа
голосов .
-
вида агитации . Влиянием не контролируемых
факторов обусловлено 27% вариации числа
голосов .
б) Попарное сравнение
видов агитации по влиянию на количество
поданных голосов проведем при помощи
проверки гипотез
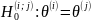 gпри
альтернативах
gпри
альтернативах
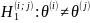
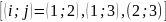 . Вычислим значения статистики
. Вычислим значения статистики
 ,
имеющей (в предположении справедливости
,
имеющей (в предположении справедливости
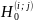 )
распределение Стьюдента с
степенями свободы ( здесь
)
распределение Стьюдента с
степенями свободы ( здесь
 .
.

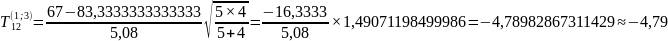

Критическая точка
распределения Стьюдента на 5%-ном уровне
значимости
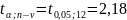 .
.
Гипотеза
 не отвергается , так как
не отвергается , так как
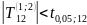 ,
то есть
,
то есть
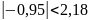 , то есть эффекты влияния первого и
второго уровней фактора на результативный
признак
, то есть эффекты влияния первого и
второго уровней фактора на результативный
признак
 одинаковы , а гипотезы
одинаковы , а гипотезы
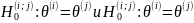 отвергаются
(так как
отвергаются
(так как
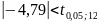 и
и
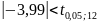 )
, то есть при переходе с первого и второго
уровня на третий эффект влияния не
изменялся .
)
, то есть при переходе с первого и второго
уровня на третий эффект влияния не
изменялся .
Пункт 4
. Оценим параметры детерминированной
модели однофакторного дисперсионного
анализа . Оценка
 параметра
параметра
 равна общему среднему
равна общему среднему
 . Оценка
. Оценка
 эффекта
эффекта
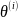 влияния
влияния
 -ого
уровня ыфактора
-ого
уровня ыфактора
 равна
равна
 , то есть
, то есть
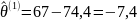 ;
;
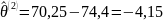 ;
;
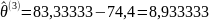 ;
;
Оценка параметра
 равна
равна
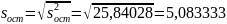 .
.

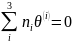
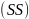
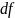 )
)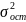 , (
, (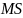 )
)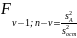
 -значение
-значение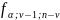
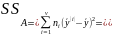 821,5166
821,5166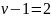
 =410,75
=410,75 310,083
310,083

 1131,6
1131,6