
Раздел 4 Построение маршрутных матриц
Ответы на ключевые вопросы:
Задача о нахождении кратчайшего по длине пути в связывающей сети относится к фундаментальным задачам комбинаторной оптимизации.
Путем называется последовательность вершин, соединяющих пару вершин графа. Путь из вершины в вершину, имеющий минимальную возможную длину, называется кратчайшим путем. Связывающей называется сеть, если в ней для каждой пары вершин имеется один соединительный путь.
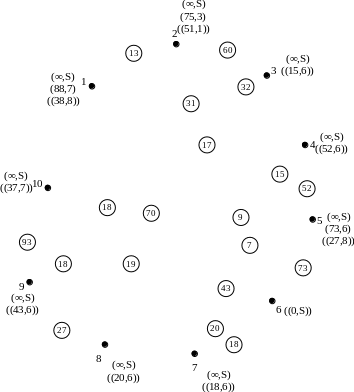
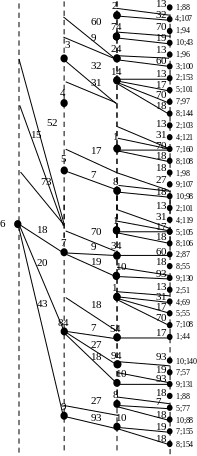
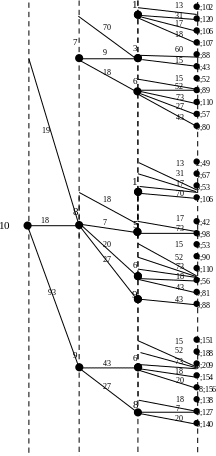
Алгоритм Дейкстрызаключается в том, что в нем одновременно строятся кратчайшие пути из заданной вершины во все остальные вершины сети.
В алгоритме Дейкстры используются временные и постоянные пометки. Временные могут изменяться, а постоянные не изменяются.
Под транзитными пунктами понимают узлы коммутации, встречающиеся в пути следования сообщения.
Ярусные деревья – пути от некоторых заданных вершин к остальным вершинам графа.



Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
– |
13 |
– |
31 |
17 |
– |
– |
18 |
– |
– |
Т=1 |
– |
63/4 |
73/2 |
45/1 |
25/8 |
38/8 |
– |
24/5 |
45/8 |
36/8 |
Т=2 |
– |
132/3,7 |
53/6,8 |
90/6,8 |
111/6,8 |
44/8,5 |
55/10,8 |
103/6,4 |
51/8,5 |
42/8,5 |



Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
13 |
– |
60 |
32 |
– |
– |
– |
– |
– |
– |
Т=1 |
63/4 |
– |
– |
44/1 |
30/1 |
75/3 |
69/3 |
31/1 |
– |
– |
Т=2 |
139/7,3 |
– |
92/7,1 |
127/6,3 |
38/8,1 |
51/8,1 |
93/6,3 |
37/5,1 |
58/8,1 |
88/7,3 |



4; 104
31
1
5; 90
17
7; 143
13
70
2
4
8; 91
32
18
1; 123
31
6; 144
52
13
31
1; 98
32
4
2; 99
17
1; 105
52
5
8; 95
73
7
70
3
6
1; 103
15
19
7
10; 52
18
8
1; 53
20
18
5; 42
43
7
9
9; 62
27
18
10; 53
27
8; 85
10; 151
93
9
2; 92
4; 110
13
31
1
5; 96
70
17
8; 97
4; 79
52
18
7
6
5; 100
18
15
8; 47
20
9; 70
19
43
18
10
8; 46
9; 121
93
Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
– |
60 |
– |
– |
– |
15 |
9 |
– |
– |
– |
Т=1 |
26/2 |
– |
– |
45/2 |
88/6 |
27/7 |
33/6 |
35/6 |
58/6 |
28/7 |
Т=2 |
53/8,6 |
92/1,7 |
– |
104/1,2 |
42/8,6 |
144/4,2 |
143/1,2 |
46/10,7 |
62/8,6 |
52/7,6 |


3; 104
60
2
73
5
6; 121
8; 55
13
7
1
7
3; 110
17
9
8
6; 119
70
18
188
10; 120
19
5; 56
7
20
31
6; 69
27
9; 76
18
17
10; 67
1
5; 62
70
7; 115
13
18
8; 63
6; 107
15
4
2
3
32
60
9
7; 101
60
2; 127
9
3
7; 76
17
52
1; 142
15
5
8; 132
7
70
6
1; 140
73
3; 79
9
7
10; 89
18
19
8
1; 90
20
18
5; 89
43
7
9
9; 99
27
18
10; 90
27
8; 122
10; 188
93
Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
31 |
32 |
– |
– |
– |
52 |
– |
– |
– |
– |
Т=1 |
45/2 |
44/1 |
67/6 |
– |
48/1 |
– |
70/6 |
49/1 |
95/6 |
– |
Т=2 |
140/7,6 |
127/3,6 |
79/7,6 |
– |
56/8,1 |
69/8,1 |
76/3,6 |
55/5,1 |
76/8,1 |
67/8,1 |

6; 55
20
2
4
7
8
3; 90
2; 80
6; 100
3; 96
6; 105
10; 106
9; 62
10; 53
13
31
70
18
60
32
52
9
18
19
27
18
4; 62
32
1
17
6
3
4
7
8
9
2; 148
7; 97
1; 156
2; 157
1; 161
10; 110
1; 111
9; 120
10; 111
8; 143
10; 209
9
52
18
20
43
60
9
31
32
70
19
18
27
18
27
93
3; 100
9
5
73
7
2; 38
13
1
18
4; 56
31
6
9
10
3; 42
4; 79
7; 45
9; 70
6; 77
10; 127
7; 44
9; 118
52
43
18
93
43
19
15
7; 95
70
8
20
27
18
93
Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
17 |
– |
– |
– |
– |
– |
– |
7 |
– |
– |
Т=1 |
25/8 |
30/1 |
82/6 |
48/1 |
– |
27/8 |
87/1 |
35/1 |
34/8 |
25/8 |
Т=2 |
111/8,6 |
38/1,8 |
42/6,8 |
56/1,8 |
– |
55/8,1 |
44/10,8 |
143/9,6 |
62/8,1 |
53/8,1 |
Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
– |
– |
15 |
52 |
– |
– |
18 |
20 |
43 |
– |
Т=1 |
83/4 |
75/3 |
27/7 |
– |
27/8 |
– |
24/3 |
70/9 |
47/8 |
37/7 |
Т=2 |
44/5,8 |
51/1,8 |
100/2,4 |
69/1,8 |
55/1,8 |
– |
57/10,8 |
55/10,7 |
107/8,5 |
43/7,3 |

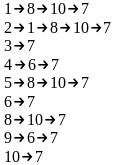

Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
– |
– |
9 |
– |
– |
18 |
– |
– |
– |
19 |
Т=1 |
– |
69/3 |
33/6 |
70/6 |
87/1 |
24/3 |
– |
37/10 |
61/6 |
– |
Т=2 |
55/8,10 |
93/3,6 |
143/2,1 |
76/6,3 |
44/8,10 |
57/8,10 |
– |
44/6,3 |
64/8,10 |
56/8,6 |

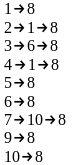
Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
18 |
– |
– |
– |
4 |
20 |
– |
– |
27 |
18 |
Т=1 |
24/5 |
31/1 |
35/6 |
49/1 |
35/1 |
70/9 |
37/10 |
– |
63/6 |
120/9 |
Т=2 |
103/4,6 |
37/1,5 |
46/7,10 |
55/1,5 |
140/6,9 |
55/7,10 |
44/3,6 |
– |
123/6,5 |
107/7,1 |

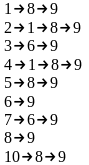
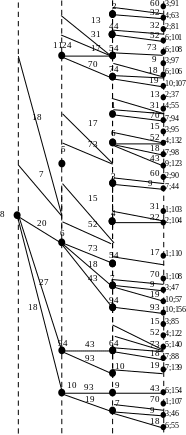
3
2;118

60
7;67



4

1;126
2;127
8;123
3;70
10;80
1;81
2;58
5;62
1;51
6;107
5;120
7;65
7;64
1;182
3;121
5;118
6;131
5
6

1;133
27
93
17


7
1;131



8

5;70

10;81
43
15
52
73
18
20
9
31
32
7
70
9
19
18
7
18
13
31
17
70
17
73
15
52
73
18
18
7
20
18
19
18
19
1
4;76

7;115
9
5

8


3;62
6


4;99



10
7
10
8

70
9
18
18
7
20
6;130


1;129


Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
– |
– |
– |
– |
– |
43 |
– |
27 |
– |
– |
Т=1 |
45/8 |
– |
58/6 |
95/6 |
34/8 |
47/8 |
61/6 |
63/6 |
– |
45/8 |
Т=2 |
51/5,8 |
58/1,8 |
62/6,8 |
76/1,8 |
62/1,8 |
107/5,8 |
64/10,8 |
123/5,6 |
– |
80/7,6 |


Т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Т=0 |
– |
– |
– |
– |
– |
– |
19 |
18 |
– |
– |
Т=1 |
36/8 |
– |
28/7 |
– |
25/8 |
37/7 |
– |
120/9 |
45/8 |
– |
Т=2 |
42/5,8 |
49/1,8 |
52/6,7 |
67/1,8 |
53/1,8 |
43/3,7 |
53/6,8 |
57/6,7 |
80/6,7 |
– |
