
- •Var Имя_массива : array [нач_индекс .. Кон_ивдекс] of Тип_данных;
- •1. Вычисление суммы (суммирование) элементов вектора
- •2. Вычисление произведения элементов вектора
- •Пример 3
- •3. Вычисление произведения двух векторов
- •10. Алгоритм поиска максимального (или минимального) элемента вектора
- •11. Алгоритм сортировки (упорядочивания) элементов вектора
- •12. Вычисление полинома по схеме горнера
11. Алгоритм сортировки (упорядочивания) элементов вектора
Сортировка означает перестановку элементов вектора в определенном порядке (по возрастанию или по убыванию) в соответствии с их значениями.
Рассмотрим алгоритм сортировки (упорядочивания) элементов вектора, когда значение каждого последующего элемента вектора больше предыдущего. Например, пусть исходный вектор X={ }6=(3, 4, 2, -1, 6, 0), тогда в результате сортировки получим вектор X=(-1, 0, 2, 3, 4, 6).
Существуют различные способы решения данной задачи. Рассмотрим один из них.
Процедура сортировки элементов вектора X по возрастанию их значений следующая.
Первый шаг
Среди N-1
элементов вектора X
(за исключением
![]() )
произведем поиск минимального элемента
вектора
)
произведем поиск минимального элемента
вектора
![]() и поменяем его
местами с первым элементом, если значение
<
.
В результате выполнения первого шага
сортировки получим следующий вектор
X=(-1,
4, 2, 3, 6, 0).
и поменяем его
местами с первым элементом, если значение
<
.
В результате выполнения первого шага
сортировки получим следующий вектор
X=(-1,
4, 2, 3, 6, 0).
Второй шаг
Среди N-2 элементов
вектора X (за
исключением
,
![]() )
произведем поиск минимального элемента
вектора
и поменяем его
местами со вторым элементом, если
значение
)
произведем поиск минимального элемента
вектора
и поменяем его
местами со вторым элементом, если
значение
![]() <
.
В результате выполнения второго шага
сортировки получим вектор X=(-1,
0, 2, 3, 6, 4).
<
.
В результате выполнения второго шага
сортировки получим вектор X=(-1,
0, 2, 3, 6, 4).
Очевидно, после выполнения N-1 шага (в нашем примере после 5 шагов) получим окончательный упорядоченный вектор X=(-1, 0, 2, 3, 4, 6).
Алгоритм упорядочивания по возрастанию элементов вектора показан на рис. 22. Данный алгоритм пригоден для упорядочивания элементов вектора по убыванию с очевидной заменой знака " > " на знак " < " в блоке проверки условия (рис. 22).
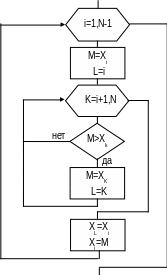
Рис.22
12. Вычисление полинома по схеме горнера
Дан полином PN(x) порядка N.
y
= PN(x)=![]() (
18 )
(
18 )
Порядок N, значение
аргумента
![]() и коэффициенты
и коэффициенты
![]() (
(![]() )
известны. Поставим задачу разработки
эффективной схемы вычисления полинома
y = PN(
).
)
известны. Поставим задачу разработки
эффективной схемы вычисления полинома
y = PN(
).
Представим уравнение (18) в следующем виде:
![]() (
19 )
(
19 )
Очевидно, уравнение Горнера (19) предполагает меньший объем арифметических операций, чем исходное уравнение (18).
Рассмотрим следующую процедуру вычисления полинома с использованием рекуррентной формулы (рис. 24):
![]() ,
,
![]() для
для
![]() . (
20 )
. (
20 )
Действительно,
для
![]()
![]()
для
![]()
![]() (
21 )
(
21 )
. . . . . . . . . . . . . . . . . . . . . .
для
![]()
![]() =PN(
)
=PN(
)
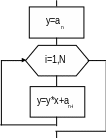
Рис.24. Алгоритм вычисления полинома по схеме Горнера.
