
- •Var Имя_массива : array [нач_индекс .. Кон_ивдекс] of Тип_данных;
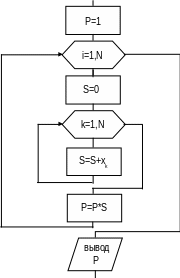
- •1. Вычисление суммы (суммирование) элементов вектора
- •2. Вычисление произведения элементов вектора
- •Пример 3
- •3. Вычисление произведения двух векторов
- •10. Алгоритм поиска максимального (или минимального) элемента вектора
- •11. Алгоритм сортировки (упорядочивания) элементов вектора
- •12. Вычисление полинома по схеме горнера
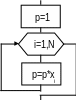
1. Вычисление суммы (суммирование) элементов вектора
Для вычисления
суммы
![]() элементов
вектора, предположим, X
= {
элементов
вектора, предположим, X
= {![]() },
i
= 1, 2, ..., N,
его значения и размерность N
должны быть
известны как
для данного случая, так и для последующих
задач.
},
i
= 1, 2, ..., N,
его значения и размерность N
должны быть
известны как
для данного случая, так и для последующих
задач.
Очевидно,
Алгоритм суммирования элементов вектора приведен на рис. 5.
Отметим, что
начальное значение суммы
Покажем, как можно использовать данный типовой алгоритм для реше-ния более сложной задачи.
|
Рис.5 |
Пример 2
Необходимо
вычислить средне- арифметическое
значение
Алгоритм примера 2 показан на рис. 6.
|
Рис.6 |
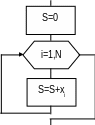
2. Вычисление произведения элементов вектора
Алгоритм для вычисления произведения элементов вектора приведен на рис. 7.
Отметим,
что начальное значение произведения
|
Рис.7 |
Пример 3
Н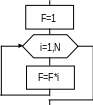 еобходимо
вычислить значение произведения
еобходимо
вычислить значение произведения
![]() (факториала)
натурального ряда целых чисел от 1 до
N.
(факториала)
натурального ряда целых чисел от 1 до
N.
Следовательно,
Схема алгоритма для вычисления факто-риала показана на рис. 8.
|
Рис.8 |
Пример 5
Дан вектор X = { }, i=1, 2, ..., N. Необходимо вычислить значение Р согласно следующему выражению:
P
=
![]()
![]() k.
( 6 )
k.
( 6 )
Например, если N = 4 тогда
P
=
![]()
Графическая схема алгоритма данной задачи представлена на рис. 11.


Вычисление
суммы
S=
![]()

Рис.11
3. Вычисление произведения двух векторов
i=1, 2, ..., N . Отметим, что размер обоих векторов равен N, а результатом произве-дения двух векторов будет число
C
= A
* B
=
Алгоритм вычисления произведения двух векторов приведен на рис. 12.
|
Рис. 12 |
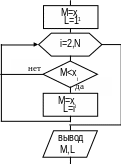
10. Алгоритм поиска максимального (или минимального) элемента вектора
Дан вектор X={ }N .
Необходимо найти
элемент вектора Х
, имеющий максимальное значение. Например,
пусть X
= (3, 4, 2, -1, 6,
0). Очевидно, что M(max)
=![]() =
6; L
(порядковый номер максимального
элемента)=5.
=
6; L
(порядковый номер максимального
элемента)=5.
Процедура поиска максимального элемента вектора следующая: предположим, что максимальным является первый элемент, т.e. M=a1, L=1.
Алгоритм поиска максимального элемента вектора показан на рис. 21. Данный алгоритм пригоден для поиска минимального элемента вектора при очевидной замене знака "<" на знак ">" в блоке проверки условия (рис. 21).
|
Рис. 21 |

 ( 2 )
( 2 )
 Очевидно,
Очевидно,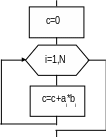 Даны
два вектора
A
= {ai}
и B
= {bi},
Даны
два вектора
A
= {ai}
и B
= {bi},
 Затем
каждый элемент
,
Затем
каждый элемент
,