§ 5. Площа в полярних координатах

_{Якщо неперервна крива задана в полярних координатах рівнянням ρ= ρ(φ), то площа сектора, обмеженого дугою кривої і двома полярними радіусами, які відповідають значенням , буде виражена інтегралом:}

Приклад. Знайти площу, яка знаходиться всередині лінії _{(ламініската Бернуллі).}

_{Зробимо малюнок:}

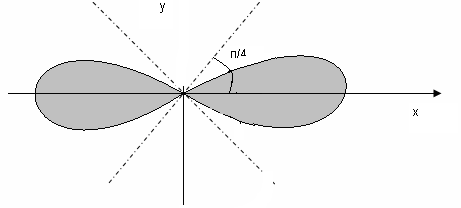
_{Враховуючи симетрію фігури, можна знайти площу четвертої частини фігури:}

_{Звідси: S = a}²_{(кв. од.)}

_{Обчислити площу фігури, обмеженої лініями:}

§ 6. Об’єми тіл обертання

_{Об’єми тіл, утворених обертанням криволінійної трапеції, обмеженої кривою у =f(x) віссю Ох і двома вертикалями x = a ; x = b навколо осей Ох і Оу виражаються формулами:}

_або

Приклад №1.

Обчислити об’єм тіла, утвореного обертанням навколо осі Оу фігури, обмеженої лініями: ху = 4, х = 0; у = 1; у = 6.

Розв’язання: Зробимо малюнок.

_{- гіпербола.}

_{хy = 4, тобто .}

_.

_{Виконати завдання:}

1. Знайти об’єм тіла, утвореного обертанням навколо осі Ох еліпса 4х²+9у²-36 = 0.

2. Обчислити об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої лініями: 3х-2у+6 = 0, х = 1, у = 0.

3. Обчислити об’єм фігури, утвореного обертанням навколо осі Оу фігури, обмеженої лініями: у = -х²+4, х = 0, у = 0, у = 3.

4. Обчислити об’єм тіла, утвореного обертанням навколо осі Оу фігури, обмеженої лініями: у = х², 2х –у = 0.

5. Обчислити об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої лініями: .

§7. Довжина дуги кривої

Довжина дуги гладкої кривої між двома точками з абсцисами і знаходиться за формулою:

Якщо гладка крива задана рівнянням в полярних координатах, то довжина дуги дорівнює:

,

де α і β – значення полярного кута в крайніх точках (α<β).

Приклад. Знайти довжину дуги кривої між точками x = 0 і .

Оскільки ,

, то

Знайти довжину дуги кривої:

1) y² = x³ від початку координат до точки В(4;8).

2) y = arcsin(e^-x) від х = 0 до х =1.

3) між точками перетину лінії з віссю Ох.

4) (всієї лінії).

5) (всієї лінії).

6) 9y² = x(x-3)² між точками перетину з віссю Ох.

§8. Площа поверхні обертання

Площа поверхні, утвореної обертанням навколо осі Ох дуги кривої знаходиться за формулою:

Знайти площу поверхні, утвореної обертанням навколо осі Ох кривої:

1) від х = 1 до х = 7.

2) y = tgx від x = 1 до x = a (a > 1)

3) y = sinx (однієї напівхвилі)

4) (a > b)

5) 9y² = x(3-x)² від х = 0 до х = 3.

§9. Застосування визначеного інтеграла для розв’язування фізичних задач

1. Шлях, пройдений точкою.

Якщо точка рухається по деякій кривій і абсолютна величина її швидкості є функцією від часу t, то шлях точки, пройдений за час знаходиться за формулою:

2. Робота сили.

Якщо змінна сила F = f(x) діє в напрямі осі Ох, то на проміжку робота цієї сили:

3. Статичні моменти дуги кривої.

Якщо маса рівномірно розподілена по дузі кривої y = f(x), (з лінійною густиною ρ = 1), то статичні моменти Mx і My цієї дуги відносно осей Ох і Оу знаходяться за формулами:

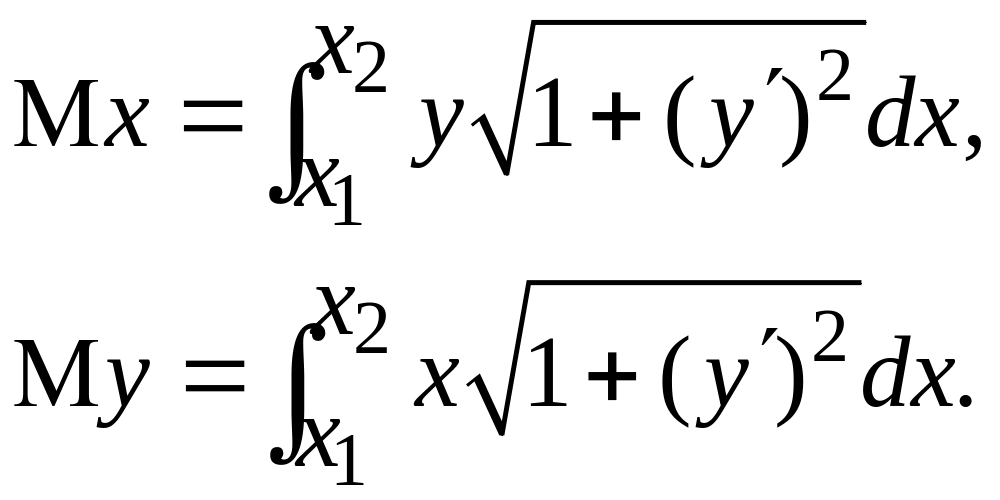
4. Центр ваги дуги кривої:

5. Статичні моменти криволінійної трапеції.

Статичні моменти Мх і Му криволінійної трапеції, обмеженої кривою y=f(x), віссю Ох і двома вертикалями х = х₁ і х = х₂ обчислюються за формулами:

6. Центр ваги криволінійної трапеції.

Координати центра ваги криволінійної трапеції (маса розподілена рівномірно, лінійна густина ρ = 1) з такими ж заданими умовами (п.4) знаходяться так:

Розв’язати задачі:

1. Швидкість точки задається формулою м/с. Знайти шлях, пройдений точкою за перші 10 сек. Після початку руху.

2. Два електричних заряди знаходяться на осі Ох відповідно в точках х₀ = 0 і х₁ = 1 см. Яку роботу буде виконано, якщо другий заряд переміститься в точку х₂ = 10 см _?

3. Вертикальна гребля має форму трапеції. Обчислити силу тиску води на греблю, якщо відомо, що верхня основа греблі a = 70 м., нижня основа b = 50 м., висота греблі h = 20 м. ( Прим. Для обчислення сили тиску рідини використовують закон Паскаля: , де Р – сила тиску рідини на площадку площею S, δ – густина рідини, h – глибина занурення, g – прискорення сили тяжіння).

4. Обчислити статичні моменти відносно осей Ох і Оу і координати центра ваги відрізка прямої ,який знаходиться між осями координат.

5. Обчислити статичні моменти відносно осей Ох і Оу і координати центра ваги фігури, обмеженою синусоїдою y = sinx і відрізком осі Ох від точки х = 0 до точки х = π.