5. Поняття елементарної функції. Класифікація елементарних функцій.

Озн. Елементарною ф-цією назив. ф-ція, яку можна задати одним аналітичним виразом, складеним з елементарних ф-цій і сталих за допомогою скінченного числа арифметичних операцій (додавання, віднімання і ділення) і скінченного числа операцій взяття ф-ції від ф-ції.

Класифікація елементарних функцій:

1. Цілі раціональні функції:

Функція представляється , многочлен n-го степеня з дійсними коефіцієнтами;

2. Дробово-раціональні функції: Відношення двох таких многочленів

, , .

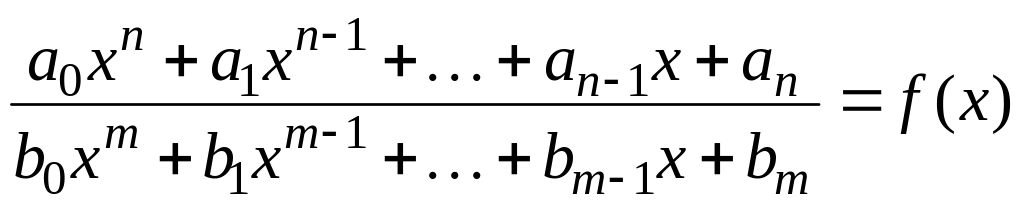Ці два класи функцій об’єднані в один клас раціональних функцій.

3.Ірраціональні функції. Це функції, в яких, крім вказаних вище дій, використовується

операція добування кореня.

Раціональні та ірраціональні функції входять до більш загального класу алгебраїчних функцій. Всі інші елементарні функції називаються трансцендентними:.

Основні елементарні функції:

1.Степенева функція: , де n – дійсне число:

(α=n – натуральний показник)

: Область визначення D(f)=R; Область значення E(f)=[0;+ ).

: Область визначення D(f)=R; Область значення E(f)=R.

(α=n – цілий від’ємний показник)

: Область визначення D(f)=(-∞;0)U(0;+ )=R\{0}; Область значення E(f)=(0;+ )

: Область визначення D(f)=(-∞;0)U(0;+ )=R\{0};D(f)=(-∞;0)U(0;+ )=R\{0}.

2. Показникова функція: , де a – додатне число, відмінне від 1:

при a>1: Область визначення D(y)=R; Область значення E(y)=(0;+ );

при 0<a<1: Область визначення D(y)=R; Область значення E(y)=(0;+ ).

3. Логарифмічна функція: , де основа логарифма a-додатне число, відмінне від 1

при a>1: Область визначення D(y)=(0;+ ); Область значення E(y)=R;

при 0<a<1: Область визначення D(y)=(0;+ ); Область значення E(y)=R.

4. Тригонометричні функції: , , , а також , , ;

: Область визначення D(sinx)=R; Область значень E(sinx)=[-1;1].

: Область визначення D(cosx)=R; Область значень E(cosx)=[-1;1].

: Область визначення ; Область значень E(tgx)=R.

: Область визначення ; Область значень E(ctgx)=R.

5. Обернені тригонометричні функції: , , , а також , , .

: Область визначення D(arcsinx)=[-1;1]; Область значень E(arcsinx)=[ ].

: Область визначення D(arccosx)=[-1;1]; Область значень E(arccosx)=[0;π].

: Область визначення D(arctgx)=(-∞;∞); Область значень E(arctgx)=( ).

: Область визначення D(arcctgx)=(-∞;∞); Область значень E(arcctgx)=(0;π).

Існують і неелементарні функції. Це, наприклад, y=sign x.

6. Границя послідовності. Властивості збіжних послідовностей.

Послідовністю називається функція натурального аргумента, тобто коли кожному натуральному числу ставиться у відповідність дійсне число.

Послідовність називається зростаючою (спадною) , коли при збільшенні (зменшенні) члени послідовності зростають (зменшуються), тобто якщо при ( ).

Число називається границею послідовності якшо для довільного існує таке натуральне число , яке залежить від , що для всіх виконується нерівність .

Теорема1. Якщо послідовність має границю, то ця границя єдина.

Доведення.

Припустимо супротивне. Нехай послідовність має дві границі . Виберемо a<b . Візьмемо довільне , таке, щоб . Знайдемо числа і , при яких , а для . Якщо вибрати N більшим з чисел N₁ N₂ , то і , що неможливо, тому що .

Теорема 2. Якщо послідовність має границю, то вона обмежена.

Доведення.

Нехай . Тоді в будь-який окіл точки потрапляють всі за винятком хіба лише скінченного числа точок. Нехай, починаючи з , всі потрапили до околу . Виберемо з чисел найбільше за модулем М. Тоді для . Виберемо . Тоді для , тобто послідовність -- обмежена.

Теорема 3. Якщо для послідовностей і , що мають скінченні (не обов'язково) границі і , і починаючи з деякого номера для всіх наступних членів виконуються нерівності або , то .

Теорема4. Якщо з трьох послідовностей , , дві мають одну й ту саму границю , і при всіх , починаючи з деякого номера, справджуються нерівності , то .

Дійсно, нехай дано . Оскільки , то існує таке , що , Оскільки , то існує таке , що . Нарешті , нехай нерівності справджуються при всіх . Виберемо тепер . Тоді всі нерівності справджуватимуться одночасно : , , , звідси , або . Це означає, що .

Послідовність називається нескінченно малою , якщо її границя дорівнює нулю.

Теорема 5. Сума скінченного числа нескінченно малих послідовностей є нескінченно мала послідовність.

Теорема6. Добуток обмеженої послідовності на нескінченно малу послідовність є послідовність нескінчено мала.

Теорема 7. Для того, щоб послідовність мала границю, яка дорівнює , необхідно і достатньо, щоб існувала така нескінченно мала послідовність , що .

Теорема 8. (про границю суми). Якщо послідовності і , то послідовності мають границі, причому Доведення.