1. Множина дійсних чисел. Упорядкованість та щільність множини дійсних чисел.

Спочатку, у процесі лічби виникає натуральний ряд чисел . Різні арифметичні операції призводять до розширення цього класу. Тому вводиться число і цілі від’ємні числа, а потім і раціональні. Далі з’являються ірраціональні і комплексні числа. Всі раціональні та ірраціональні числа складають множину дійсних чисел. Множина дійсних чисел позначається .

Властивості дійсних чисел:

1. Операція додавання: Для будь-якої впорядкованої пари дійсних чисел визначено, причому єдиним чином, число, що називається їх сумою і позначається 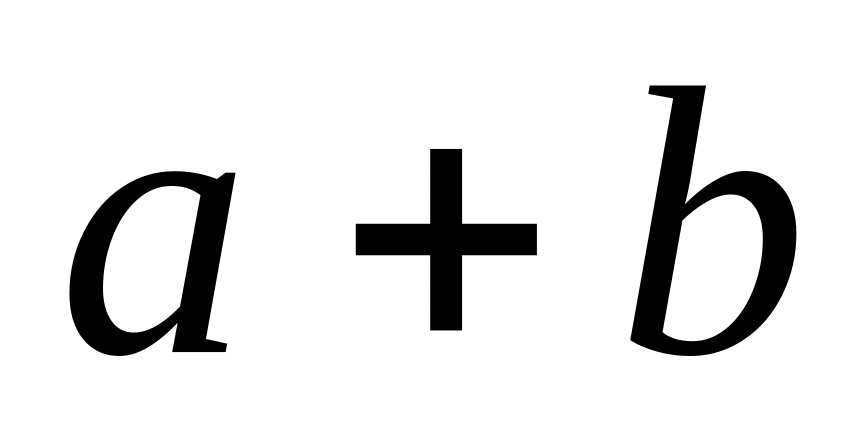. При цьому мають місце наступні властивості:

а) Для будь-якої пари чисел і

- переставний або комутативний закон додавання

б) Для будь-якої трійки чисел , ,

- асоціативний закон додавання

в) Існує число таке, що для будь-якого числа

г) Для будь-якого числа таке, що

2. Операція множення: Для будь-якої впорядкованої пари чисел і визначено, причому єдиним чином, число, що називається їх добутком і позначається 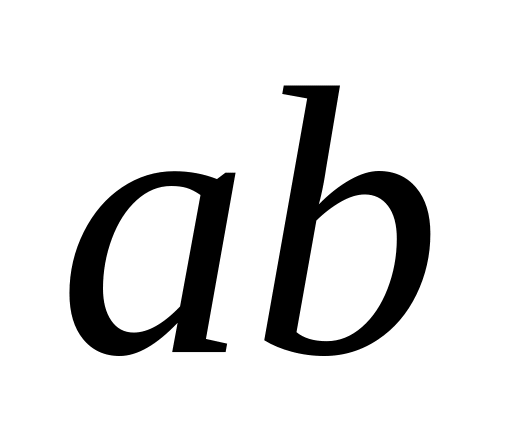. При цьому мають місце наступні властивості:

а) Для будь-якої пари чисел і

- переставний або комутативний закон множення

б)

в)

г)

3. Зв’язок між операціями додавання і множення

4. Впорядкованість: Для кожного числа визначено одне із відношень 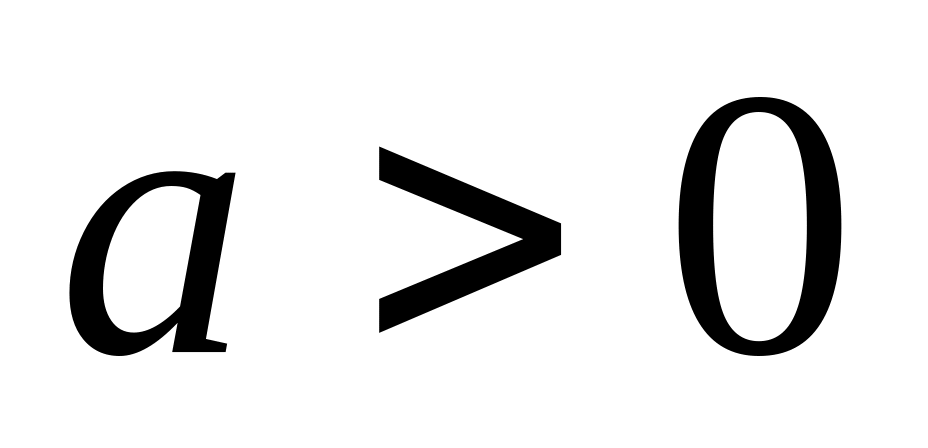, , 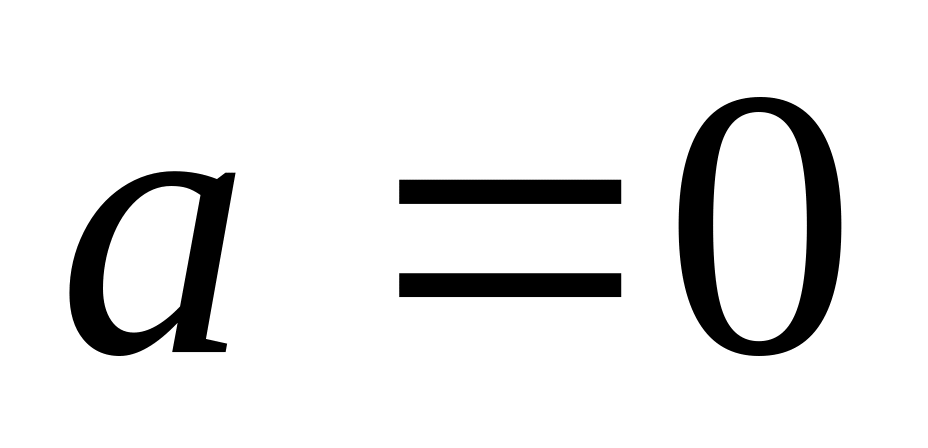, 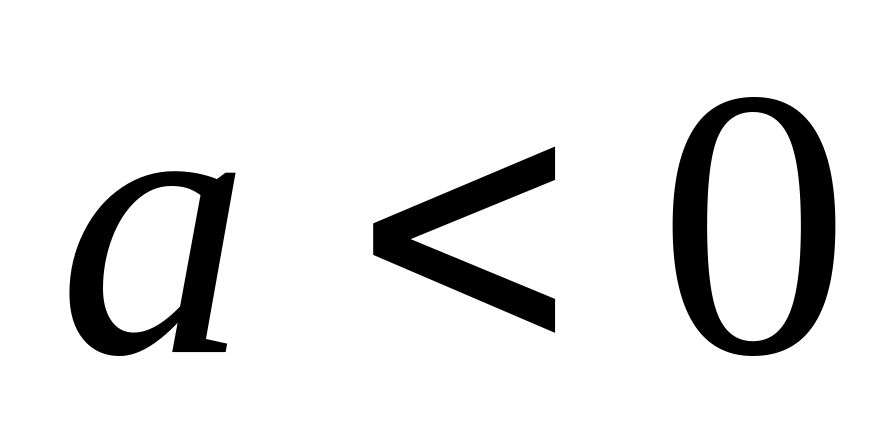при цьому, якщо і 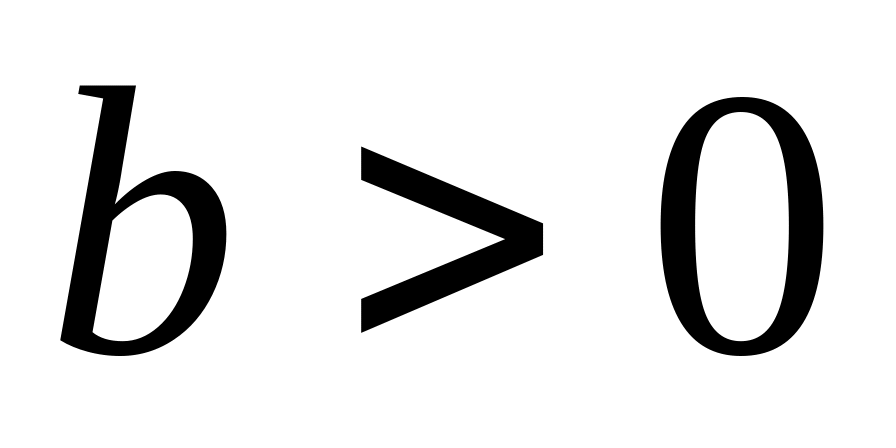, то

а)

б)

Якщо , то

5. Властивість неперервності дійсних чисел: Для кожного перерізу 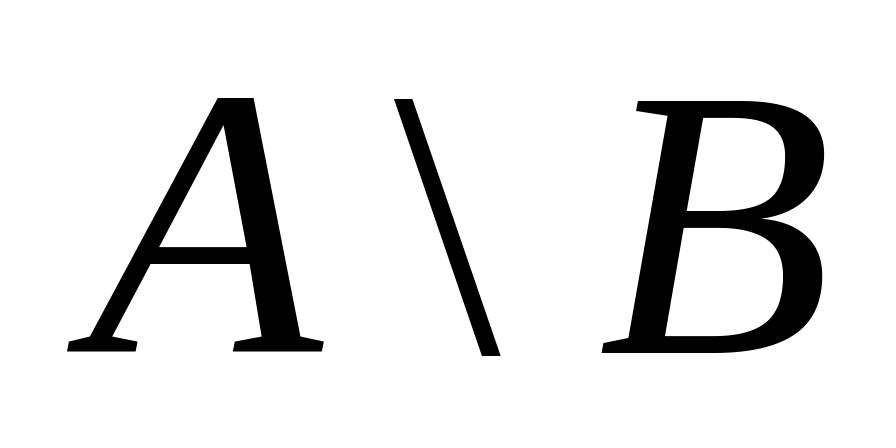множини дійсних чисел існує число , що породжує цей переріз,

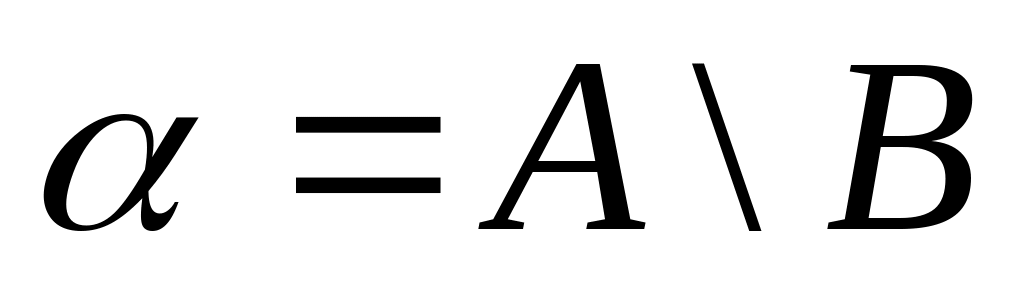
2. Теорема Дедекінда. Для всякого перерізу в множині дійсних чисел існує число , що породжує цей переріз і якщо належить нижньому класу, то в ньому воно найбільше, якщо належить верхньому класу, то воно в ньому найменше.

Доведення. 1) . Нехай

Те, що є найбільше число в класі видно із формули, що задає число множину .

Покажемо, що в множині немає найменшого числа. Припустимо супротивне: нехай в є найменше число. Позначимо його через . Оскільки , то за другою формулою . Звідси, , тобто . Звідси за другою формулою маємо . Аналогічно із маємо , тобто . Прийшли до суперечності.

2) Доводиться аналогічно.

3. Грані, точні грані множини. Теорема про існування точних граней.

Властивості точних граней.

Означення верхньої межі множини: Якщо дійсне число таке, що для будь-якого слідує , то говорять, що число є верхньою межею множини . Якщо є одна верхня грань, то ми можемо знайти їх безліч. Найменша серед всіх верхніх граней множини називається точною верхньою гранню і позначається .

Означення нижньої межі множини: Якщо дійсне число таке, що для будь-якого слідує , то – нижня грань множини . Якщо є одна нижня грань, то ми можемо знайти їх безліч. Найбільша серед всіх нижніх граней множини називається точною нижньою гранню і позначається .

Теорема про існування точних граней: 1) Якщо множина обмежена зверху, то вона має точну верхню грань.

2) Якщо множина обмежена знизу, то вона має точну нижню грань.

Доведення 1):Розглянемо обмежену зверху множину , це означає, що знайдеться число , що для всіх . Треба довести що існує . I) В множині є найбільше число , то для всіх , , тому – верхня грань і найменша серед верхніх граней, має супремум. .

II) немає найбільшого числа, тому множину розіб’ємо на два класи: в віднесемо всі верхні грані множини , саму множину і решту чисел віднесемо в клас . Видно, що таке розбиття є переріз в . За теоремою Дедекінда цей переріз породжується деяким межовим числом . Але в немає найбільшого, бо в не було найбільшого, тому . За теоремою Дедекінда воно найменше., разом з тим воно є верхньою гранню, то

Доведення 2): Розглянемо множину обмежену знизу. Це означає, що знайдеться число , що для всіх . Треба довести, що існує . I) В множині є найменше число , то для всіх , тому – нижня грань і найбільша, має серед нижніх граней, має інфінум

II) У множині немає найменшого числа. Зробимо переріз в множині . До класу віднесемо всі нижні грані. До класу віднесемо множину і решту чисел. За теоремою Дедекінда існує межове число , яке породжує переріз . не попало в , бо в нема найменшого. Тоді – нижньому класу і там воно найбільше, а нижній клас складається з нижніх граней. Тому серед нижніх граней воно є найбільшим. Тому . Теорема доведена.

Властивості точних граней. 1) Нехай множина має – точну верхню грань. , то

1)

2) Яке б ми не взяли число , то ,

2) Нехай множина має – точну нижню грань. , то

1)

2) Якщо , то , .

Множина, яка обмежена знизу і з верху називається обмеженою. Є множини не обмежені не зверху ні знизу – . Може бути множина обмежена знизу, але не обмежена зверху: . Бувають множини необмежені знизу, але обмежені зверху: .