2.4 Лінійні диференціальні рівняння із змінними коефіцієнтами -го порядку.

Нехай (1). Зробимо заміну незалежної змінної і з’ясуємо за яких умов ми зможемо одержати рівняння зі сталими коефіцієнтами: (2). Підставляємо (2) в (1): ; ; … ; .

. (3)

Поділимо (3) на . Отримаємо .

Необхідно, щоб . .

Рівняння Ейлера: .Якщо ,тобто , то дане рівняння задовольняє умовам т. Пікара-Коші, а –особлива точка. Побудуємо загальний розв’язок рівняння Ейлера для (якщо то всюди замінюємо на ).

, . Отже, ( ). Підставляємо:

; ; = ;…; .

.

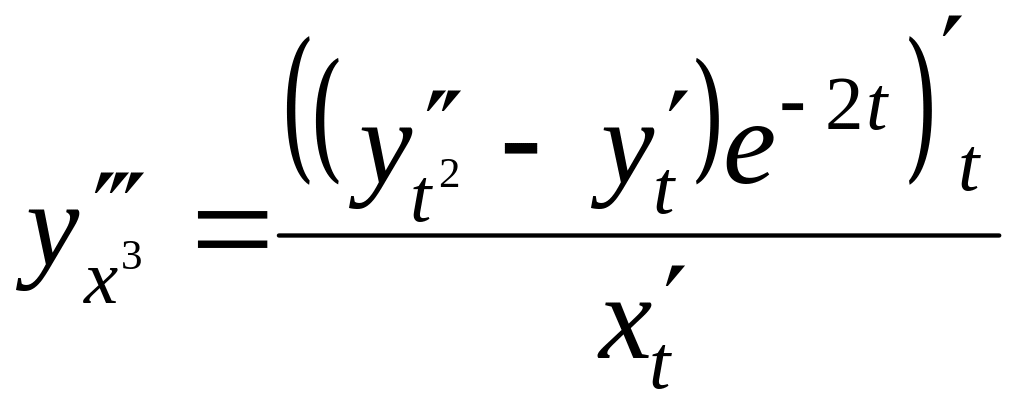Експоненти знищуються, після чого відносно функції одержимо рівняння зі сталими коефіцієнтами. Розв’язавши його, потрібно повернутися до змінної за формулою .

Рівняння Лагранжа: . Заміна : – отримаємо рівняння Ейлера; – рівняння зі сталими коефіцієнтами.

Рівняння Чебишова: . На –розв’язок існує і єдиний. Розв’яжемо рівняння Чебишова на інтервалі .

.

. Отже, ( ). Підставляємо: ; .

.

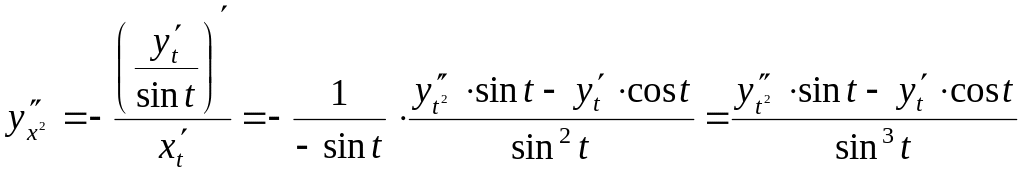; ; . Отже, .

3.1 Методи розв’язування лінійних однорідних систем.

3.2 Методи розв’язування лінійних неоднорідних систем.

Структура загального розв’язку лінійної неоднорідної системи.

Розглянемо лінійну неоднорідну систему

(1)

Припустимо, що відомий деякий частинний розв’язок цієї сис­теми у₁ = у₁⁽¹⁾ , у₂ = у⁽₂¹⁾ , ..., у_п = у_n⁽¹⁾, а отже, (2)

Введемо нові невідомі функції

за формулами

(3)

Підставляючи (3) в систему (1), одержуємо

(4)

Врахо Враховуючи (2), з (4) для відшукання функцій маємо лінійну однорідну систему

(5)

Систему (5) називають однорідною системою, яка відповідає неод­норідній системі (1).

Згідно з основною теоремою загальний розв’язок однорідної системи (5) визначається формулою (6)

Де - деяка ФСР цієї системи, а – довільні сталі. Підставляючи (6) в (3), одержуємо (7)

Формула (7) визначає загальний розв’язок системи (1) в усій області її задання. Таким чином, для знаходження загального розв’язку неоднорідної системи (1) достатньо знайти будь-який частинний розв’язок цієї системи і додати до нього загальний розв ’язок відповідної однорідної системи (5).

2. Метод варіації довільних сталих (метод Лагранжа). Якщо відома фундаментальна система розв'язків лінійної однорідної системи (5), то загальний розв’язок неоднорідної системи (1) може бути знайдений у квадратурах. Це можна зробити, наприклад, за допомогою методу варіації довільних сталих (методу Лагранжа), суть якого полягає у наступному.

Розв’язок лінійної неоднорідної системи (1) шукаємо у вигляді (8)

Де - деяка ФСР однорідної системи (5), а – деякі неперервно диференційовні функції.

Виберемо функції , так, щоб формула (8) визначала розв’язок системи (1). Підставляючи (8) в (1), одержуємо:

,

Оскільки - ФСР однорідної системи (5), то вираз в дужках в (9) дорівнює нулю, а тому для відшукання функцій , маємо систему (10)

Визначник системи (10) відмінний від нуля для всіх (ним є вронскіан ), а тому ця система має єдиний розв’язок: (11)

- алгебраїчне доповнення елемента вронскіана . Інтегруючи (11), знаходимо

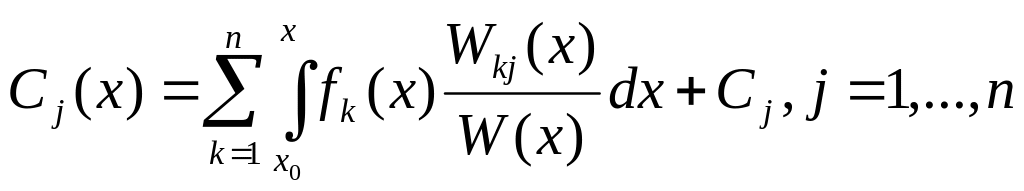
де - довільні сталі, а - довільна точка з інтервалу .

Підставляючи ці значення у формулу (7), одержуємо

Якщо підставити тут С₁ = С₂ =... = С_п = 0, то маємо розв’язок

(12)

а тому (12) можна записати у вигляді (7) і, отже, розв’язок, визначений формулою (14), є загальним розв’язком неоднорідної системи (1).

Таким чином, проблема інтегрування лінійної неоднорідної системи зводиться до необхідності побудови фундаментальної системи розв'язків відповідної однорідної системи. Тому особливий інтерес мають такі лінійні системи рівнянь, у яких фундаментальна система розв'язків відповідної однорідної системи виражається через елементарні функції. До таких систем належать перш за все системи зі сталими коефіцієнтами.

3. Метод невизначених коефіцієнтів розв’язування лінійних неоднорідних систем зі сталими коефіцієнтами. Розглянемо лінійну неоднорідну систему диференціальних рівнянь зі сталими коефіцієнтами

(13)

Якщо праві частини системи (13) є квазімногочленами, тобто складаються з сум і добутків многочленів , функцій то розв’язок цієї системи можна шукати методом невизначених коефіцієнтів. Це робиться за тими ж правилами, як й для одного лінійного рівняння зі сталими коефіцієнтами, проте з деякими змінами. А саме:

1. Якщо - де 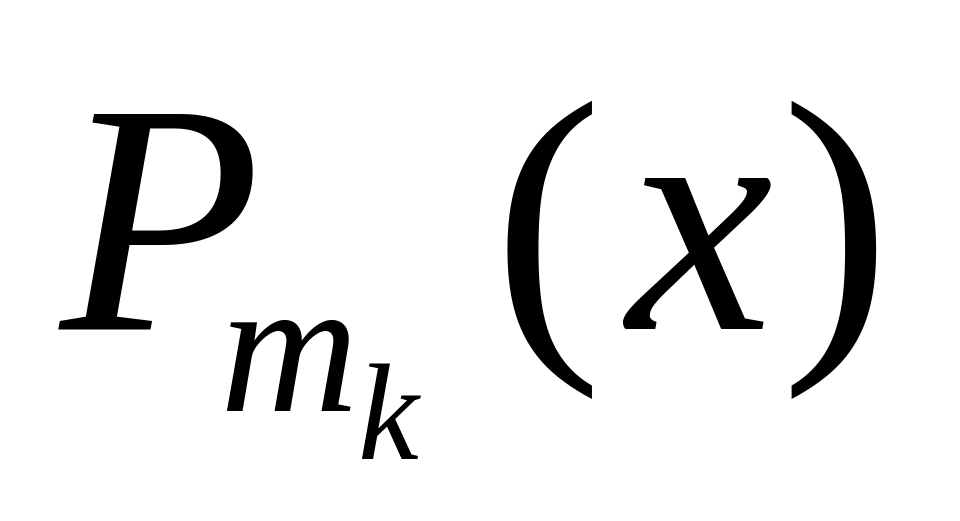многочлен степеня 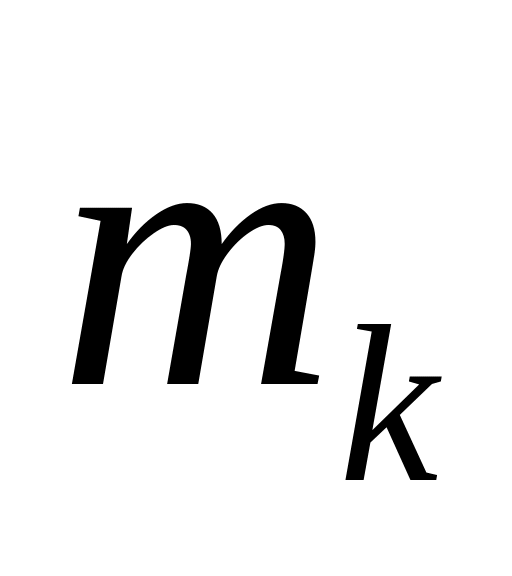, то частинний розв’язок системи (1) потрібно шукати у вигляді

(14)

де - многочлени степеня з невідомими коефіцієнтами, , якщо - не характеристичне число; якщо ж є характеристичним числом, то замість можна взяти кратність цього кореня (або, якщо точніше, число на одиницю більше найвищого з степенів многочленів, на які множаться в загальному розв’язку відповідної однорідної системи).

Невідомі коефіцієнти многочленів визначаються після прирівнювання коефіцієнтів біля подібних доданків після підставляння виразів (14) у (13).

2. Аналогічно визначаються степені многочленів й у випадку, коли праві частини містять функції , а число є характеристичним.