2.2 Лінійні однорідні рівняння зі сталими коефіцієнтами

Нехай маємо - ф-цій. Якщо співвідношення (1) виконується тотожно тільки в випадку, коли , то ф-ції назив. Лінійно незалежними.

Якщо спів. (1) виконується , коли хоча б один з коефіцієнтів відмінний від 0 ( ), то вказані ф-ції є лінійно залежними.

Нехай маємо ф-ції кожна з яких є -1раз диференційовна. Складемо з цих ф-цій визначник :

.Цей визначник назив. визначником Вронського, або вронскіаном.

Необхідна умова лінійної залежності ф-ції.

Теорема1. Якщо ф-ції є лінійно залежними на інтервалі , то в кожній точці цього інтервалу.

- лін.зал.

( ) -лін.незалежні

Дов. З того, що - лінійно залежні . При чому хоч один з коефіцієнтів відмінні від 0. Нехай (інакше цього можна добитися перепозначенням сталих), тоді . Підставимо в вронскіан

.Цей визначник дорівнює 0, бо якщо розкласти його на суму визначників, то всі ці визначники міститимуть пропорційні стовпці, а отже дор.0.Теорема дов.

Дана умова є тільки необхідною, тобто з того що вронскіан тотожно дор. 0 не випливає лінійна залежність ф-цій .Нехай розв. р-ня (2) з неперервними коефіцієнтами на .

Теорема2. Якщо - лінійно незалежні розв. р-ня (2) з неперервними коеф. На , то в кожній точці інтервалу.

Дов. Припустимо, що . Побудуємо систему: - тривіальний розв’язок. 3(прод.) Визначником даної системи є . Оскільки за припущенням , то дана система має нетривіальний розв. . Утворимо ф-цію . Оскільки ф-ція є лінійною комбінацією розв. р-ня (2) , то вона сама є розв. цього р-ня. Крім того ця ф-ція задовольняє такі початкові умови . Справді (3). Але ці самі умови задовольняє ф-ція . За теоремою Пікара при неперервних коефіцієнтах р-ня (2) існує єдиний розв. задачі Коші (2)(3). Таким чином . При чому хоча б один з коефіцієнтів відмінний від 0. З останньої рівності випливає, що ф-ції лінійно залежні, що суперечить умові теореми. Доведено, що .

2.3 Лінійні неоднорідні рівняння (метод варіації довільних сталих, метод невизначених коефіцієнтів) Метод варіації довільних сталих.

Покажемо, що загальний розв'язок неоднорідного рівняння (1)

можна знайти у квадратурах, якщо відомий загальний розв'язок відповідного однорідного

рівняння: (2). Цей метод називають методом варіації довільних сталих або методом Лагранжа.

Отже, нехай знайдено загальний розв'язок лінійного однорідного рівняння, тобто

(3)

де – деяка фундаментальна система розв'язків рівняння (2), а – довільні сталі.

Загальний розв'язок рівняння (1) шукаємо у вигляді (3), розглядаючи не як довільні сталі, а як функції змінної x, тобто

(4)

Виберемо функції так, щоб вираз (4) був загальним розв'язком рівняння (1).

Диференціюючи (4), одержуємо

Виберемо функції так, щоб

Тоді матиме такий самий вигляд, як і для випадку сталих , тобто

Диференціюючи ще один раз, одержуємо

Нехай

Тоді

Продовжуючи диференціювати далі і добираю так, щоб

Одержуємо

Диференціюючи ще один раз, знаходимо

Підставимо у рівняння (1) знайдені вирази для . Тоді

Множники, що містяться в дужках біля , тотожно дорівнюють нулю, оскільки функції є частинними розв'язками рівняння (2). Отже, останнє рівняння запишемо у вигляді .

Таким чином, функції повинні задовольняти умови

тобто маємо систему n лінійних алгебраїчних рівнянь з n невідомими . Оскільки визначником цієї системи є вронскіан W( x ), відмінний від нуля для всіх , то система

має єдиний розв'язок, який можна знайти, наприклад, за формулами Крамера:

де – алгебраїчне доповнення елементів n-го рядка вронскіана W( x ).Звідси

де – довільні сталі, а – довільна точка з інтервалу .

Підставляючи знайдені вирази для функцій у формулу (4), одержуємо

(5)

Підставляючи в (5) , одержуємо частинний розв'язок неоднорідного рівняння (1):

тобто (5) можна записати у вигляді , а отже, розв'язок (5) є загальним розв'язком рівняння (1).

Легко перевірити, що частинний розв'язок (10) задовольняє нульові початкові умови, тобто

Метод невизначених коефіцієнтів розв. лінійних р-нь -го порядку зі сталими коефіцієнтами.

(1), - сталі, - неперервна на . . Характеристичне р-ня . Для розв. р-ня (10 можна викор. метод варіації довільних сталих , але для реалізації цього методу, необхідно шукати квадратури, що ускладнює завдання. Метод невизначених коефіцієнтів цього недоліку позбавлений, але він заст. тільки для тих випадків, коли ф-ція є квазімногочленом, тобто має вигляд = , або , - многочлен степеня .Розглянемо 2 випадки

1. Нехай = (2) (3)

1. Нехай число не є коренем хар. р-ня, тобто . Тоді частинний розв. р-ня (1) можна шукати у вигляді , де - многочлен степеня і =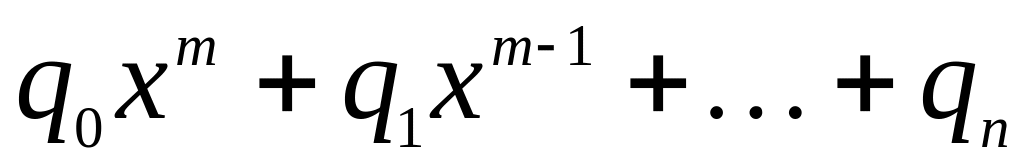 (4). Многочлен записаний з невизначеними коефіцієнтами, які шукаються прирівнюванням коеф. при однакових степенях після підстановки (4) в (1), де ф-ція має вигляд (2). Отримаємо

2. Нехай число є коренем хар. р-ня, кратності . , але . В цьому випадку частинний розв. р-ня шукаємо у вигляді (6).Підставивши (6) в попереднє р-ня і прирівнявши коеф. При однакових степенях отр.

II. = , де - числа, - многочлени степеня .

1. Якщо не є коренем хар. р-ня, то частинний розв. . Відокремлюючи дійсну та уявну частини одержуємо, що частинний розв. можна шукати у вигляді (7), де - многочлени з невизначеними коефіцієнтами, степеня кожен. Якщо в правій частині р-ня в розглянутому випадку є тільки або або , то частинний розв. р-ня всеодно шукаємо у вигляді (7).

2. Якщо є розв. хар. р-ня кратності , то частинний розв. шукаємо у вигляді (8).