1.Диф.рів-ння І порядку. Рівняння .

–загальний вигляд ДР І порядку, де F– неперервна в кожній точці деякої області . Якщо (1) можна розвязати відносно похідної, то , де – визначена та неперервна в обл. .

Функція ,визначена на проміжку наз. розвязком р-ння (2), якщо 1. 2. 3. .

Функція , яка залежить від змінної х і параметра С наз загальним розвязком р-ння (2), якщо довільний р-зок цього р-ння міститься в загальному, в тому розумінні,що він зображається у вигляді при деякому фіксованому значенні С₀ параметра С, включаючи . Розвязок,записаний у вигляді наз загальним інтегралом.

(це ДР, яке явно не містить y). Його загальний розвязок: .

( це ДР, яке явно не містить незалежної змінної).

Отже . Можливі особливі розвязки де

1.1

1.2

1.3 Рівняння в повних диференціалах. Інтегруючий множник.

Озн. ДР вигляду (1) назив. рі-ням в повних диференціалах якщо існує така неперервно-диференційовна ф-ція , що (2).

Теорема. Нехай ф-ції неперервні в однозв’язній області G, в G. Щоб рі-ня (1) було в ПД н. і д. щоб для всіх точок області G виконув. умова (3).

■Необхідність.Доведемо,що з (2) (3).Нехай виконується умова (2). З другого боку (4). З (2) і (4) -продиф.обидві ч-ни цих рі-нь по і по відповідно: , . Отже, виконується (3).

Достатність. Доведемо,що з (3) (2).Виконується умова (3). Побудуємо ф-цію для якої справджується рівність (2). Для цього розглянемо ДР розв’язавши його знаходимо , продиф. по : Вик-чи. (3) , .З . Отримали ф-цію (+С). Отже, (3) (2). ■

Якщо рі-ня (1) не є в ПД, то можна знайти таку ф-цію , що після множення на неї обох частин рі-ня (1) це рі-ня стане РПД.

Озн. Функція називається інтегрувальним множником ДР (1) якщо рівняння (2) є РПД в деякій області G.

Виведемо формулу для інтегрувального множника рі-ня (1). (2)-РПД

, . Для знаходження ф-ції μ отримали ДР з частинними похідними І порядку, розв’язати яке складніше ніж рі-ня (1). Тому розглянемо деякі частинні випадки функції .

1. Нехай , тоді , - ліва частина рі-ня ф-ція від x права ф-ція від x. , , (с=1);

2. Нехай 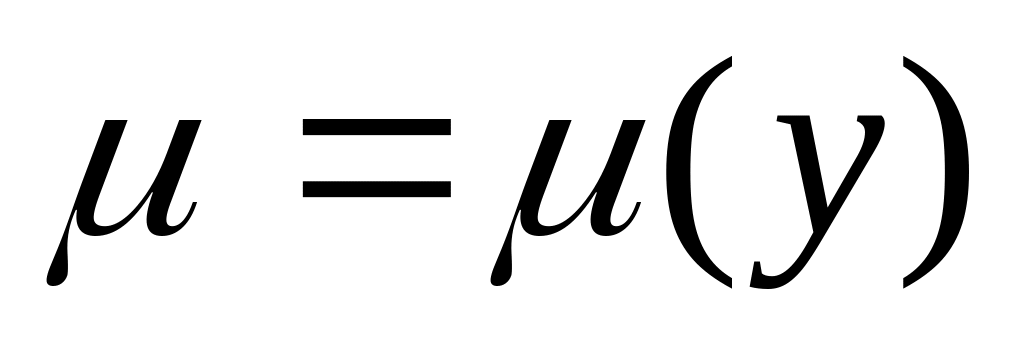, тоді , , , ;

3. , , .

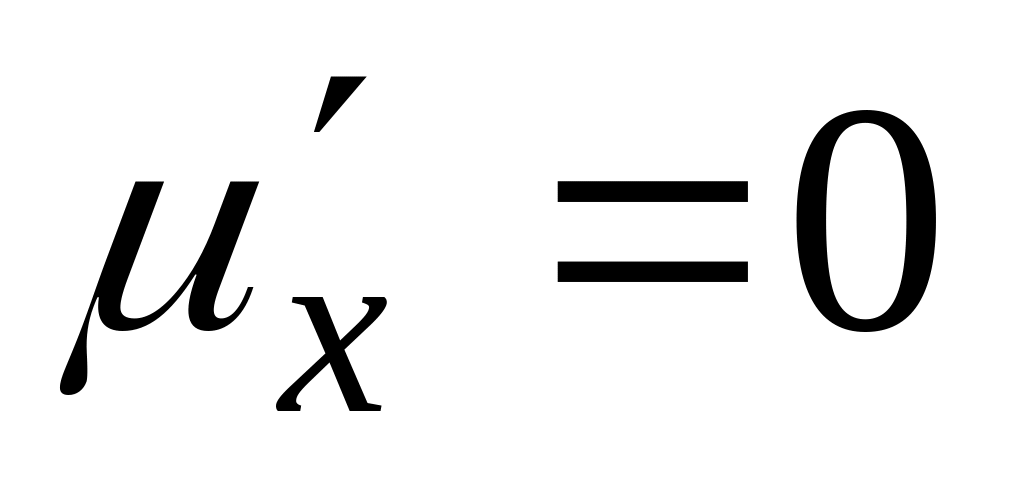
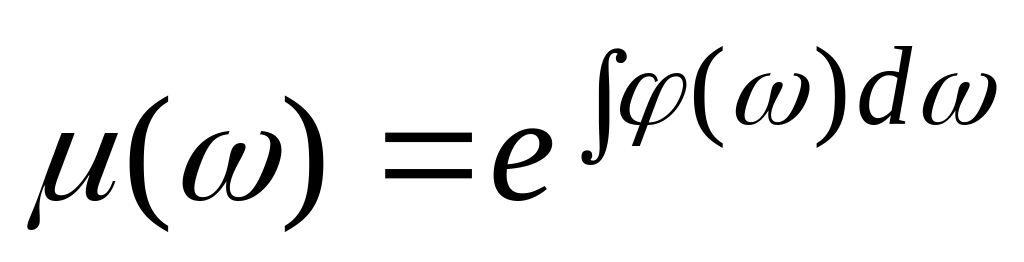Якщо μ–ін-ий мн-ик (1). особливим р-ом(1) може бути такий, при наближенні.до якого

1.4 Лінійні рівняння 1 порядку. Однорідні і неоднорідні. Рівняння Бернуллі.

Рівняння вигляду , де функції p(x) і q(x) – неперервні наз. лінійним диференціальним рівнянням 1 порядку. Якщо q(x) 0 то рівняння наз. лінійним однорідним рівнянням, якщо q(x) 0 то (1) наз. лінійним неоднорідним.

3 способи розв’язування лінійних рівнянь: 1) метод Лагранжа:

розв’язуєм рівняння (2), 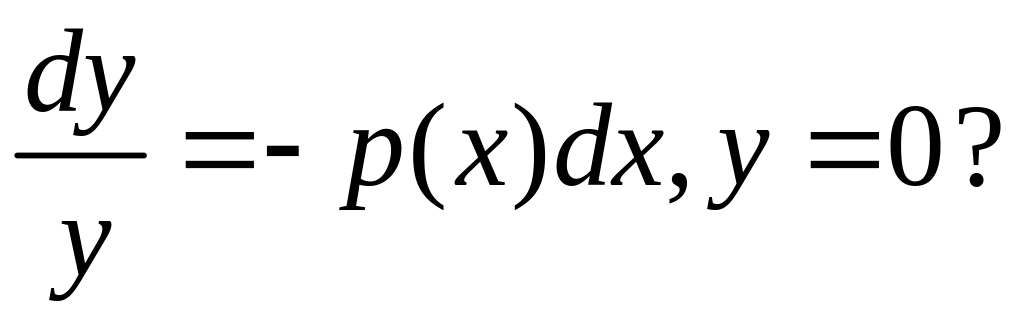, - розв’язок рівняння (2). Розв’язок у=0 є частинний, бо міститься в (3) при с=0.Розв’язок рівняння (1) шукаєм у вигляді (3) підставивши замість с неперервно – диференційовну функцію с(х). (4) , . Підставивши с(х) в (4) одержим загальний розв’язок (1): у=( ) .

2) метод Бернуллі або метод підстановки:

Розв’язок (1) шукається у вигляді y=uv (5), де u і v – довільні неперервно – диференційовні функції. Підставим в (1) , виберем v так, щоб =0, тоді . Нехай с=1, то .

3) метод інтегрувального множника, м. Ейлера:

Домножим рівняння (1) на функцію , = , у=( - загальний розв’язок.

Рівняння Бернуллі – це рівняння вигляду - неперервні функції, x є (a, b), m , m Домножим (6) на функцію (1-m) y , введем заміну z= - лінійне рівняння відносно z. Звідси , у=( . Особливі розв’язки: y=0? 1) випадок: якщо m<0 то у=0 не буде розв’язком (6); 2) вип. m>1 то у=0 можна отримати з загального розв’язку при с= ; 3) вип. 0<m<1 то степінь додатній і у=о – особливий розв’язок.

Другий спосіб розв’язання рівняння Бернуллі:

Заміна y=uv,

З першого рівняння шукається функція v і підставляється в друге рівняння, звідки знах. функція u і диференціюється.Зауваження: описані способи застосовуються також для рівняння вигляду .