
Кратные интегралы
№152. Замкнутая область
![]() называется правильной в направлении
оси
,
если любая прямая, параллельная оси
и проходящая через внутреннюю точку
области пересекает ее границу….
называется правильной в направлении
оси
,
если любая прямая, параллельная оси
и проходящая через внутреннюю точку
области пересекает ее границу….
Ответ: а) только в одной точке; б) только в двух точках;
в) не более, чем в двух точках; г) не более, чем в одной точке.
№153. Теорема о среднем. Если функция
![]() непрерывна в замкнутой области,
площадь которой равна
непрерывна в замкнутой области,
площадь которой равна
![]() ,
то внутри этой области найдется такая
точка
,
то внутри этой области найдется такая
точка
![]() ,
что:
,
что:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г) другой ответ.
;
г) другой ответ.
№154. Двойной интеграл от неотрицательной функции определяет:
Ответ: а) объем соответствующего цилиндрического тела; б) площадь полной поверхности соответствующего цилиндрического тела; в) площадь проекции соответствующего цилиндрического тела на плоскость ; г) другой ответ.
№155. Если области
- правильная в направлении оси
и ее граница задается уравнениями:
![]()
![]() ,
где
,
где
![]() ,
то формула вычисления двойного интеграла
имеет вид:
,
то формула вычисления двойного интеграла
имеет вид:
Ответ: а)
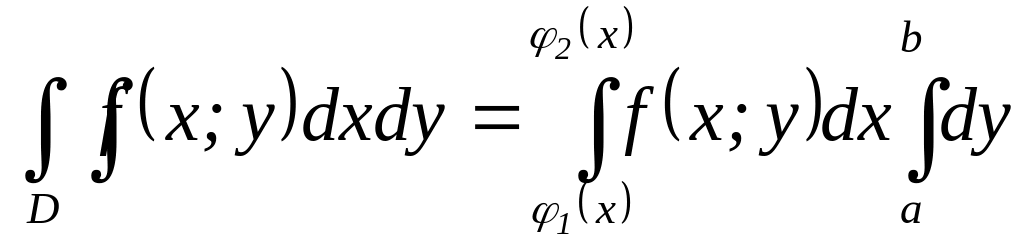 ;
б)
;
б)
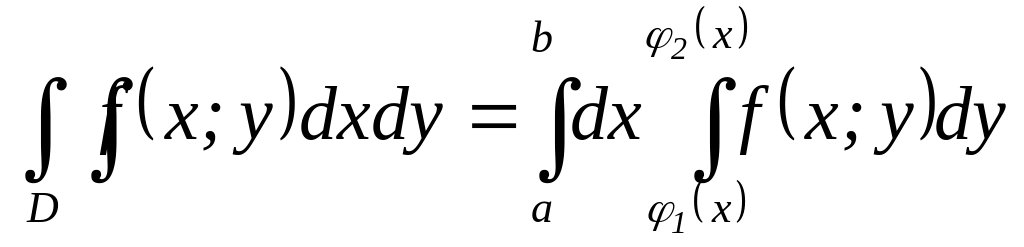 ;
;
в)
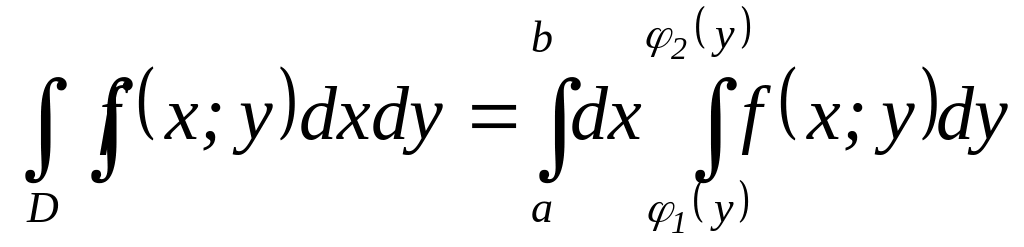 ;
г)
;
г)
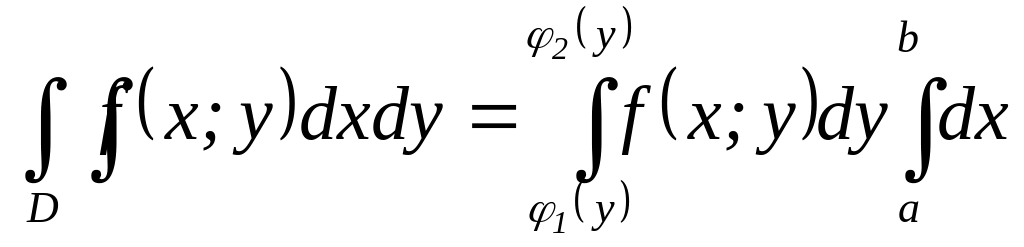 .
.
№156. Переход от декартовой к полярной
системе координат в двойном интеграле
![]() осуществляется с помощью формул:
осуществляется с помощью формул:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
№157. Площадь плоской фигуры в декартовой системе координат вычисляется по формуле:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
№158. Площадь плоской фигуры в полярной системе координат вычисляется по формуле:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
№159. Если
![]() поверхностная плотность пластины
,
то ее координаты центра масс
поверхностная плотность пластины
,
то ее координаты центра масс
![]() вычисляют по формулам:
вычисляют по формулам:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
№160. Если
поверхностная плотность пластины
,
то ее статический момент
![]() относительно оси
вычисляется по формуле:
относительно оси
вычисляется по формуле:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№161. Если
поверхностная плотность пластины
,
то ее момент инерции
![]() относительно оси
вычисляется по формуле:
относительно оси
вычисляется по формуле:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№162. Если поверхностная плотность пластины , то ее момент инерции относительно начала координат вычисляется по формуле:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№163. Если - поверхностная плотность пластины , то ее масса определяется формулой:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№164. Уравнение
![]() в пространстве задает:
в пространстве задает:
Ответ: а) параболу; б) гиперболу;
в) параболический цилиндр; г) параболоид вращения.
Построит.
№165. Уравнение
![]() в пространстве определяет:
в пространстве определяет:
Ответ: а) круговой конус; б) круговой цилиндр;
в) параболоид вращения; г) сферу.
Построить поверхность.
№166. Уравнение
![]() в пространстве определяет:
в пространстве определяет:
Ответ: а) окружность; б) сферу; в) круговой цилиндр; г) круговой конус. Построить поверхность.
№167. Уравнение
![]() в пространстве определяет:
в пространстве определяет:
Ответ: а) окружность; б) сферу; в) параболический цилиндр; г) круговой конус. Построить.
№168. Уравнение
![]() в пространстве определяет:
в пространстве определяет:
Ответ: а) круговой цилиндр; б) круговой конус; в) плоскость; г) прямую. Построить.
№169. Уравнение в пространстве определяет:
Ответ: а) прямую; б) плоскость; в) цилиндрическую поверхность; г) другой ответ.
№170. Связь декартовых и цилиндрических координат точки осуществляется с помощью формул:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
;
г)
![]() .
.
№171. Формулы связи между декартовыми координатами и сферическими имеют вид
Ответ: а)
![]() ;
б)
;
б)
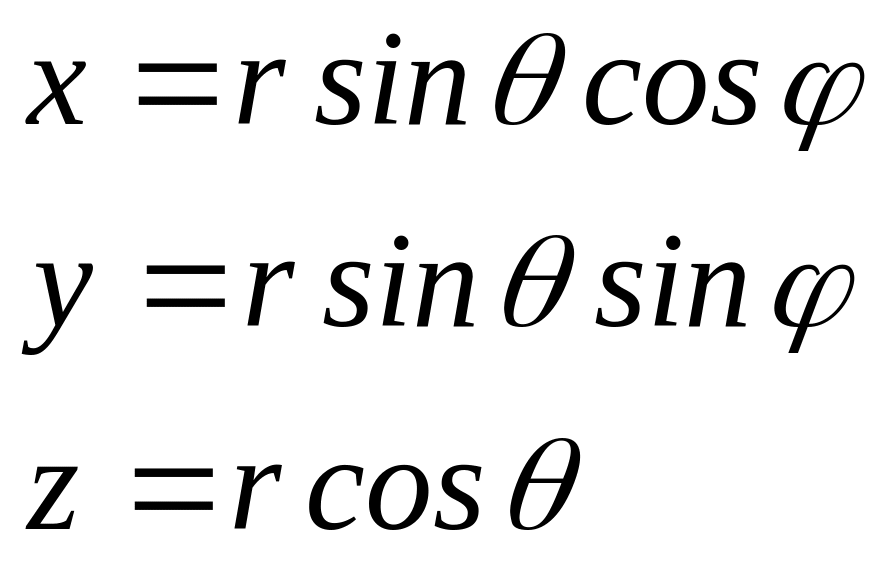 ;
в)
;
в)
![]() ;
г)
;
г)
 .
.
№172. Элемент объема в цилиндрической системе координат определяется формулой:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
№173. Элемент объема в сферической системе координат определяется формулой:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]()
№174. Если объем на плотность тела
![]() есть
есть
![]() ,
то статистические моменты тела
относительно координатных плоскостей
определяются формулами:
,
то статистические моменты тела
относительно координатных плоскостей
определяются формулами:
Ответ: а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
г) другой ответ.
;
г) другой ответ.
№175. Если объемная плотность тела есть , то моменты инерции тела относительно осей координат определяются формулами:
Ответ: а)
![]()
![]() ;
;
б)
![]()
![]() ;
;
в)
![]()
![]() ;
г) другой ответ.
;
г) другой ответ.
№176. Чему равен элемент площади
![]() в полярных координатах
в полярных координатах
![]() ?
?
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
№177. В каком случае в интеграле
![]() пределы интегрированные в повторном
интеграле будут постоянными?
пределы интегрированные в повторном
интеграле будут постоянными?
Ответ: а) - прямоугольник; б) - круг; в) - треугольник; г) другой ответ.
№178. Укажите правильную формулу перехода в двойном интеграле к полярным координатам:
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
№179. Вычислить:
![]() если
ограничена линиями
если
ограничена линиями
![]() .
.
Ответ: а) -![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
№180. Вычислить:
![]() если
ограничена линиями:
если
ограничена линиями:
![]() .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
№181. Вычислить:
![]() если
ограничена линиями:
если
ограничена линиями:
![]() .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
№182. Вычислить
![]() ,
если область
,
если область
![]() ограничена линиями:
ограничена линиями:
![]() .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() .
.
№183.Вычислить
![]() ,
если область
ограничена прямыми:
,
если область
ограничена прямыми:
![]() .
.
Ответ: а)
![]() б)
в)
б)
в)
![]() г)
г)
![]() .
.
№184. Вычислить повторный интеграл
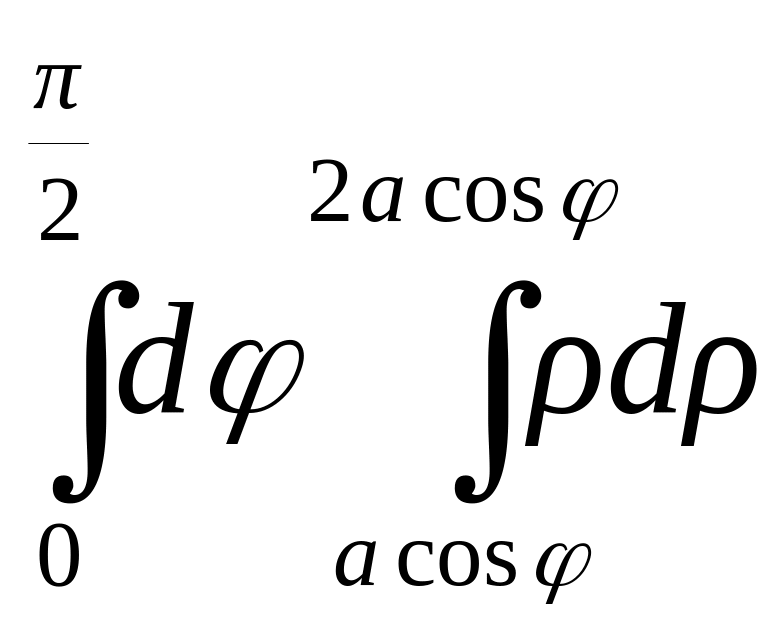 .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() .
.
№185. Вычислить двойной интеграл
![]() если
ограничена линиями
если
ограничена линиями
![]() .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
№186. Вычислить:
![]() если
ограничена линиями
если
ограничена линиями
![]() .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
№187. Вычислить площадь фигуры
,
ограниченной линиями
![]() .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() .
.
№188. Вычислить площадь фигуры,
ограниченной линиями
![]() .
.
Ответ: а)
б)
![]() в)
в)
![]() г)
г)
![]() .
.
№189.Вычислить тройной интеграл
![]()
![]() .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г)
.
г)
.
№190. Вычислить тройной интеграл
![]()
![]() .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() .
.
№191. Вычислить
![]() где область
где область
![]() определена неравенством:
определена неравенством:
![]() .
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г) другой ответ.
г) другой ответ.
№192. Вычислить
![]() ,
где
ограничена поверхностями
,
где
ограничена поверхностями
![]() ,
,
![]() .
Ответ: а)
.
Ответ: а)
![]() б)
б)
![]() в)
г) другой ответ.
в)
г) другой ответ.
№193. Вычислить
![]() где область
есть верхняя половина шара
где область
есть верхняя половина шара
![]() ,
расположенная в первом октанте.
,
расположенная в первом октанте.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г) другой ответ.
г) другой ответ.
№194. Вычислить объём, ограниченный
поверхностями:
![]()
Ответ: а)
б)
![]() в)
в)
![]() г)
г)
![]() .
.
№195. Найти массу части шара радиуса
![]() ,
расположенного в первом октанте, если
плотность в каждой точке равна расстоянию
от этой точки до плоскости
.
,
расположенного в первом октанте, если
плотность в каждой точке равна расстоянию
от этой точки до плоскости
.
Ответ: а)
![]() б)
б)
![]() в)
в)
![]() г) другой ответ.
г) другой ответ.
№196. Вычислить статический момент
относительно плоскости ХOY
полушара
![]() ,
если плотность в каждой точке
,
если плотность в каждой точке
![]() .
.
Ответ: а)
б)
![]() в)
в)
![]() г)
.
г)
.
№197. Вычислить статический момент
относительно плоскости ХOY
однородного полушара
![]() .
.
Ответ: а)
б)
![]() в)
в)
![]() г)
.
г)
.
