
Функции нескольких переменных
№ 108. Какое из определений числовой
функции
![]() наиболее точное?:
наиболее точное?:
Ответ: а) соответствие, при котором
каждой паре числовых значений
![]() отвечает только одно значение переменной
отвечает только одно значение переменной
![]() ;
б) соответствие, при котором каждой
паре числовых значений двух независимых
друг от друга переменных величин
;
б) соответствие, при котором каждой
паре числовых значений двух независимых
друг от друга переменных величин
![]() ,
отвечают значения переменной
;
,
отвечают значения переменной
;
в) соответствие, при котором каждой
паре числовых значений двух независимых
друг от друга переменных величин
![]() ,
отвечает одно и только одно значение
переменной величины
;
,
отвечает одно и только одно значение
переменной величины
;
г) числовой закон соответствия между
переменными
![]() и переменной
?
и переменной
?
№ 109. График функции
![]() это:
это:
Ответ: а) пространственная кривая; б) поверхность; в) множество точек, координаты которых удовлетворяют уравнению ; г) совокупность двух пересекающихся пространственных кривых.
№ 110. Предел функции двух переменных
![]() существует тогда и только тогда, когда:
существует тогда и только тогда, когда:
Ответ: а)
![]() независимо друг от друга; б) предел
есть одно и тоже число по любому из
направлений, идущих в точку
независимо друг от друга; б) предел
есть одно и тоже число по любому из
направлений, идущих в точку
![]() ;
в)
;
в)
![]() ;
г) другой ответ.
;
г) другой ответ.
№ 111. Продолжить определение: Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() если она определена в этой точке и ее
окрестности и если…
если она определена в этой точке и ее
окрестности и если…
Ответ: а) она ограничена в окрестности
точки; б) является бесконечно малой в
т.![]() ;
;
в)
![]() ;
г)
;
г)
![]() - конечное число.
- конечное число.
№ 112. Частной производной функции по одному из аргументов называется:
Ответ: а) предел отношения соответствующего частного приращения функции к приращению этого аргумента, если приращение аргумента стремится к нулю произвольным образом; б) предел отношения приращения функции к приращению этого аргумента, если приращение аргумента стремится к нулю произвольным образом; в) предел отношения приращения функции к приращению этого аргумента, если аргумент стремится к нулю произвольным образом; г) предел отношения соответствующего частного приращения функции к сумме приращений аргументов, если приращение каждого аргумента стремится к нулю независимо друг от друга.
№ 113. Выбрать правильный ответ и
пояснить на чертеже. Геометрически
частная производная по
функции
,
вычисленная в т.![]() ,
это:
,
это:
Ответ: а) касательная, проведенная в соответствующей точке графика данной функции;
б) угол наклона касательной, проведенной в соответствующей точке графика данной функции;
в) тангенс угла наклона касательной,
проведенной в соответствующей точке
графика данной функции; г) тангенс
угла между осью
и касательной, проведенной в соответствующей
точке графика функции к линии его
пересечения плоскостью
![]()
№ 114. Смешанные производные
![]() -го
порядка (к = 2,3,4…) функции
-го
порядка (к = 2,3,4…) функции
равны между собой, если:
Ответ: а) они непрерывны; б) функция имеет всевозможные непрерывные частные производные -го порядка и смешанные производные имеют одинаковое число дифференцирований по каждому из аргументов; в) они непрерывны и имеют одинаковое число дифференцирований по каждому из аргументов; г) они ограничены и имеют одинаковое число дифференцирований по каждому из аргументов.
№ 115. Частный дифференциал функции по одному из аргументов это:
Ответ: а) соответствующее частное приращение функции, умноженное на приращение аргумента; б) главная часть соответствующего частного приращения функции, умноженная на приращение аргумента; в) главная часть соответствующего приращения функции, линейная относительно соответствующего приращения аргумента; г) соответствующее частное приращение функции, умноженное на соответствующий дифференциал аргумента.
№ 116. Какая формула нахождения полного дифференциала функции является правильной? Объяснить все символы равенства.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)![]() .
.
№ 117. Указать правильную формулу
нахождения полной производной сложной
функции
![]() где
где
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№ 118. Указать правильную формулу
нахождения производной сложной функции
![]() ,
где
,
где
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() .
.
в)
![]() ;
г)
;
г)
![]() .
.
№ 119. Указать правильные формулы
нахождения частных производных сложной
функции
![]() ,
где
,
где
![]() .
.
Ответ: а)
![]()
![]() ;
б)
;
б)
![]()
![]() ;
;
в)
![]()
![]() ;
г)
;
г)
![]()
![]() .
.
№120. Указать правильные формулы
нахождения частных производных сложной
функции
,
где
![]() ,
,
![]() ?
?
Ответ: а)
![]()
![]() ;
;
б)
![]()
![]()
![]() ;
;
в)
![]()
![]()
![]() ;
;
г)
![]()
![]()
![]() .
.
№121. Указать правильные формулы
нахождения частных производных сложной
функции
![]() ,
где
,
где
![]() ,
,
![]() ?
?
Ответ: а)
![]() ;
;
![]() ;
;
б)
![]() ;
;
![]() ;
;
в)
![]() ;
;
![]() ;
;
г)
![]() ;
;
![]() .
.
№122. Если
![]() - неявная функция одной переменной
- неявная функция одной переменной
![]() ,
заданная равенством
,
заданная равенством
![]() ,
то какая из формул нахождения ее
производной является верной:
,
то какая из формул нахождения ее
производной является верной:
Ответ: а)
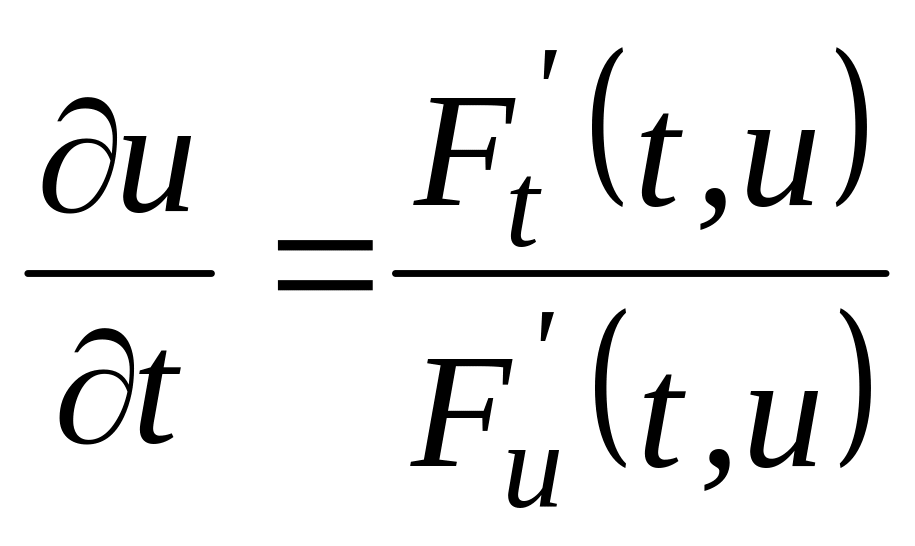 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
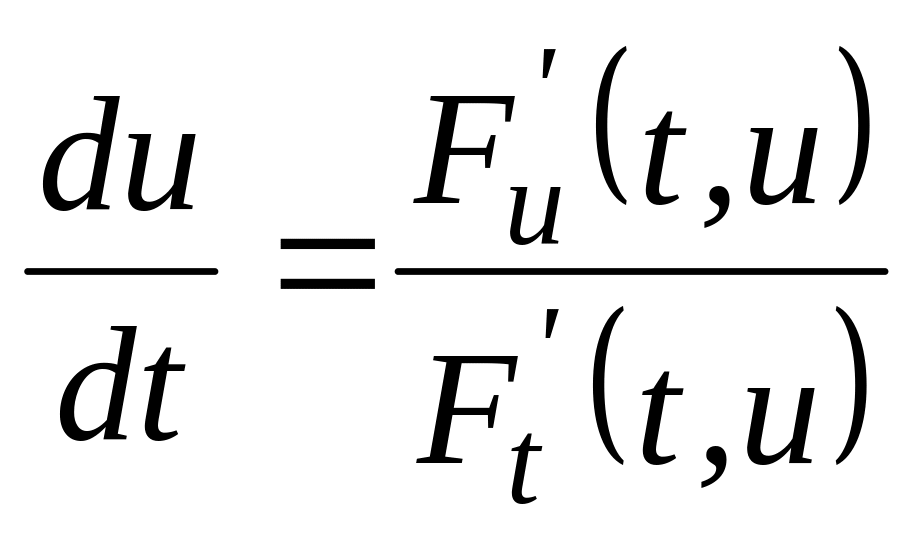 ?
?
№123. Касательная плоскость к поверхности в данной точке это плоскость:
Ответ: а) которая, имеет с поверхностью только одну общую точку; б) в которой расположены все касательные к линиям, целиком лежащими на поверхности и проходящим через одну и ту же точку; в) проходящая через две пересекающиеся касательные к поверхности в точке их пересечения; г) другой ответ
№124. Нормаль к поверхности это:
Ответ: а) нормальный вектор к поверхности; б) прямая, проходящая через начало координат перпендикулярно касательной плоскости; в) прямая, перпендикулярная касательной плоскости в точке касания; г) любой нормальный вектор к касательной плоскости.
№125. Критическая точка дифференцируемой
функции 2-х переменных
![]() это точка, в которой:
это точка, в которой:
Ответ: а) обе частные производные
1-го порядка
![]() и
и
![]() не существуют;
не существуют;
б) хотя бы одна частная производная 1-го порядка обращается в нуль или обе не существуют;
в) обе частные производные 1-го порядка обращается в нуль или хотя бы одна из них не существует; г) обе частные производные 1-го порядка обращаются в нуль.
№126. Какой из вариантов необходимого условия существования в точке экстремума функции является верным:
Ответ: а) Если в т.
обе частные производные 1-го порядка
обращаются в нуль, то т.
![]() - точка
- точка
![]() ;
б) если т.
- критическая точка функции
,
то в т.
существует
;
в) если т.
- т.
,
то в этой точке обе частные производные
1-го порядка равны нулю или хотя бы одна
из них не существует; г) если т.
- т.
,
то т.
- особая точка данной функции
;
б) если т.
- критическая точка функции
,
то в т.
существует
;
в) если т.
- т.
,
то в этой точке обе частные производные
1-го порядка равны нулю или хотя бы одна
из них не существует; г) если т.
- т.
,
то т.
- особая точка данной функции
![]() ?
?
№127. Найдите условие, позволяющее
заключить, что в стационарной точке
![]() функция
имеет максимум.
функция
имеет максимум.
Ответ: а)
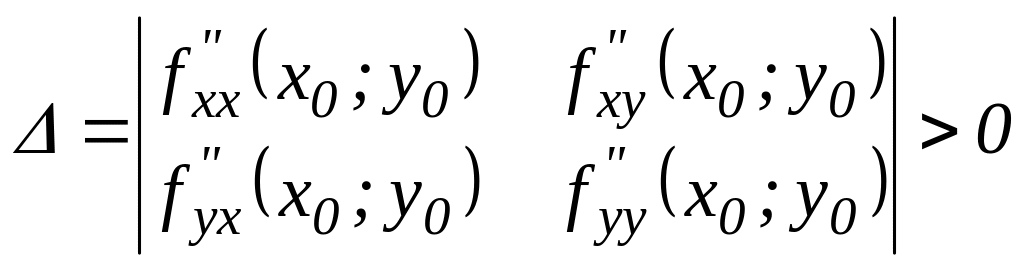 ,
,
![]() ;
;
б)
,
![]() ;
;
в)
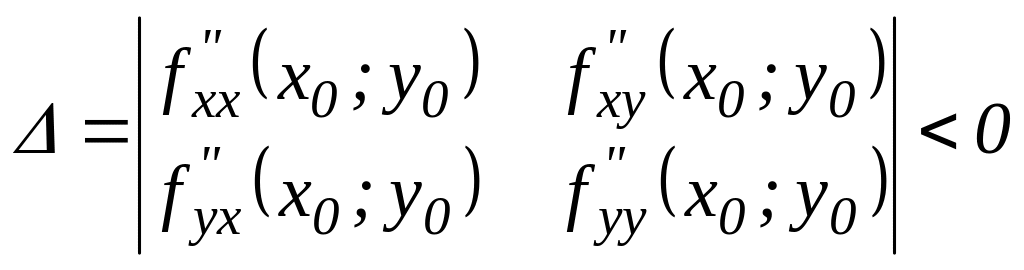 ,
,
![]() ;
;
г)
,
![]() .
.
№128. Найти и построить область
определения функции
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г) вся плоскость
;
г) вся плоскость
![]() ,
кроме точек
,
кроме точек
![]() .
.
№129. Найти и построить область
определения функции
![]() .
.
Ответ: а) Вся плоскость
,
кроме точек
![]() ;
б) вся плоскость
,
кроме точек
;
б) вся плоскость
,
кроме точек
![]() ;
;
в) вся плоскость
,
кроме точек гиперболы
![]() ;
г) вся плоскость
,
кроме точек
;
г) вся плоскость
,
кроме точек
![]() .
.
№130. Найти и построить область
определения функции
![]() .
.
Ответ: а) Вся плоскость
,
кроме точек прямых
![]() и
и
![]() ;
б) вся плоскость
,
кроме точки
;
б) вся плоскость
,
кроме точки
![]() ;
в) часть плоскость
,
лежащая между ветвями гиперболы
;
в) часть плоскость
,
лежащая между ветвями гиперболы
![]() ,
исключая ее точки; г) часть плоскость
,
лежащая между ветвями гиперболы
.
,
исключая ее точки; г) часть плоскость
,
лежащая между ветвями гиперболы
.
№131. Найти частную производную
функции
![]() по
.
по
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№132. Найти частную производную
функции
![]() по
.
по
.
Ответ: а)
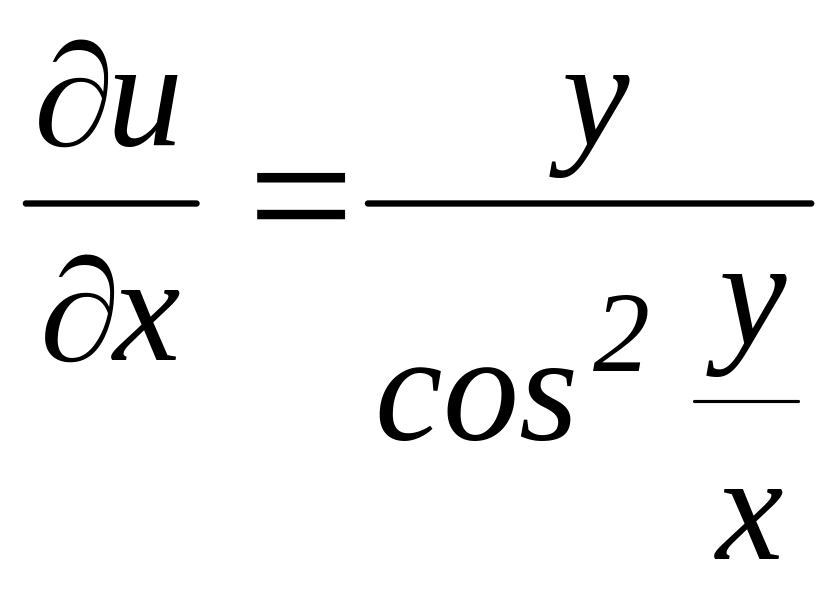 б)
б)
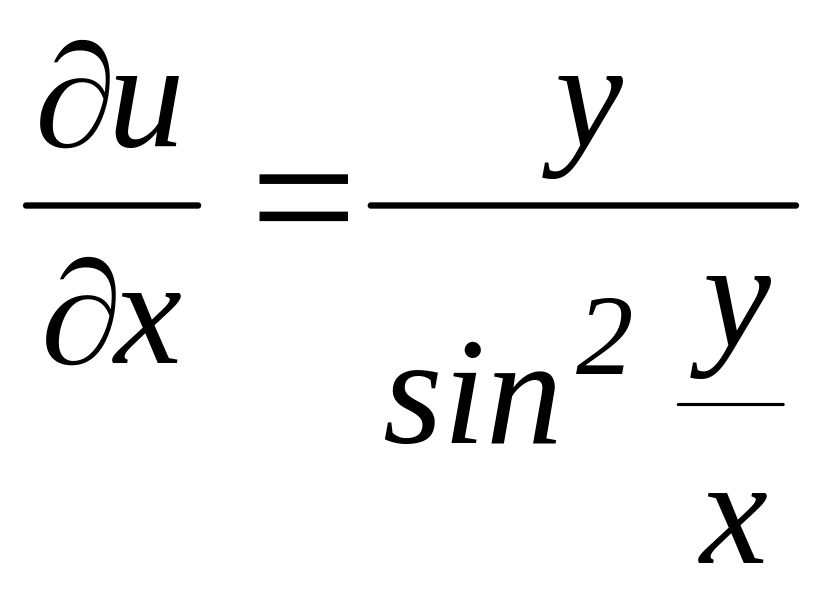 ;
в)
;
в)
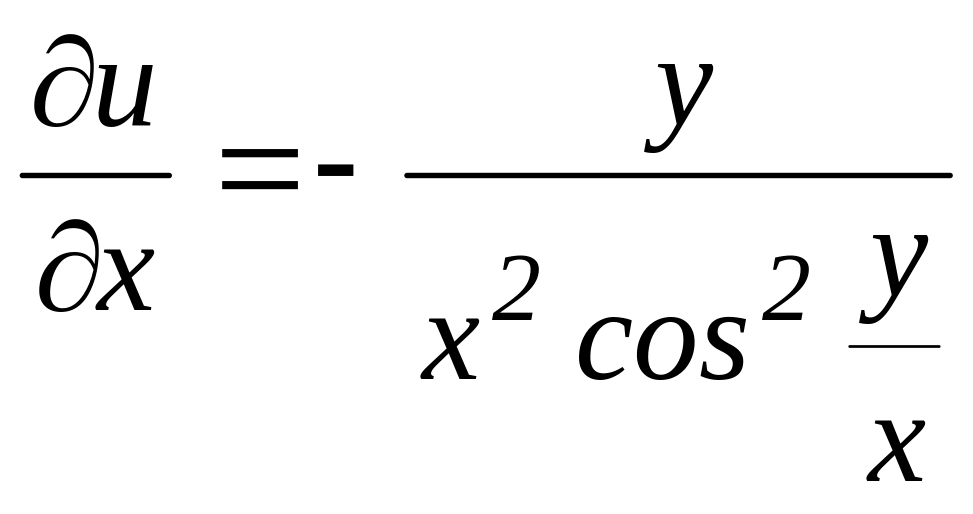 ;
г)
;
г)
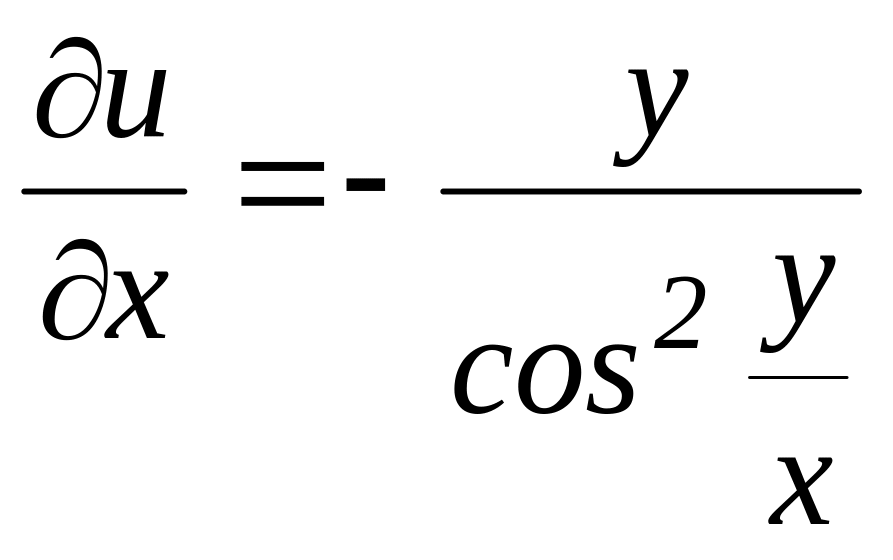 .
.
№133. Найти частную производную
функции
![]() по
.
по
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
№134. Найти частный дифференциал по
функции
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№135. Найти частный дифференциал по
функции
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№136. Найти частный дифференциал по
![]() функции
функции
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
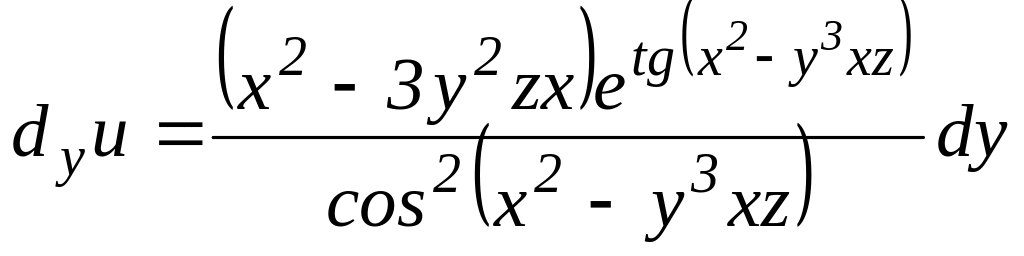 .
.
№137. Найти полный дифференциал
функции
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№138. Найти полный дифференциал
функции
![]() .
.
Ответ: а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
№139. Найти производную
![]() функции
,
заданной неявно, если
функции
,
заданной неявно, если
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
№140. Найти частную производную
![]() функции
по
,
заданной неявно, если,
функции
по
,
заданной неявно, если,
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№141. Найти частную производную по
функции
,
заданной неявно, если
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№142. Найти производную
![]() сложной функции, если
сложной функции, если
![]() ,
где
,
где
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№143. Найти производную
![]() сложной функции, если
сложной функции, если
![]() ,
где
,
где
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№144. Найти частную производную по
,
![]() ,
сложной функции, если
,
сложной функции, если
![]() ,
где
,
где
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№145. Найти частную производную по
,
![]() ,
сложной функции, если
,
сложной функции, если
![]() ,
где
,
где
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№146. Найти частную производную по
,
![]() ,
сложной функции, если
,
сложной функции, если
![]() ,
где
,
где
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
№147. Найти смешанную производную
3-го порядка
![]() функции
функции
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
№148. Составить уравнение касательной плоскости к поверхности
![]() в т.
в т.
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
№149. Составить уравнения нормали к
поверхности
![]() в точке
в точке
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
№150. Найти экстремумы функции
![]() .
.
Ответ: а)
![]() при
при
![]() ;
б)
;
б)
![]() при
;
при
;
в) экстремума нет; г)
![]() при
при
![]() .
.
№151. Найти экстремумы функции
![]() .
.
Ответ: а)
![]() при
при
![]() ;
б)
;
б)
![]() при
при
![]() ;
;
в) экстремума нет; г)
![]() при
.
при
.
