§7 Интегралы, зависящие от параметра

В том случае, если функция, стоящая под знаком определённого интеграла кроме переменной , по которой ведётся интегрирование, зависит ещё от некоторого параметра , то очевидно, что интеграл является функцией параметра , т.е.

Например ; ;

Заменим, что интегралы, зависящие от параметра, находят многочисленные приложения. Представляет интерес вопрос о существовании и нахождении производной от такого интеграла по параметру . Приведём без доказательства теорему.

Теорема. Если функция непрерывна в замкнутом прямоугольнике и имеет в нём непрерывную частную производную по параметру , то на промежутке имеем:

(1)

Заметим, что эта операция называется дифференцированием под знаком интеграла.

Отметим, что при , т.е. для несобственных интегралов для дифференцирования под знаком интеграла не достаточно сходимости интеграла и существования непрерывной частной производной . Дополнительно требуется так называемая равномерная сходимость несобственного интеграла. Рассмотрим это понятие подробнее.

Определение 1. Несобственный интеграл по неограниченному промежутку называется равномерно сходящимся по параметру на , если для любого найдётся такое, не зависящее от число , что для любого неравенство

будет выполняться для всех значений из промежутка .

Определение 2. Несобственный интеграл от неограниченной функции называется равномерно сходящимся по параметру на промежутке , если для любого найдётся такое, не зависящее от число , что для любого неравенство

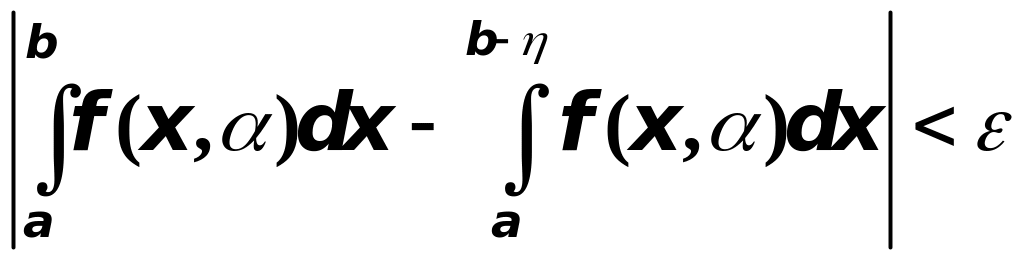
выполняется для всех значений из промежутка .

Существует простой признак равномерной сходимости по параметру несобственных интегралов, который мы приведём без доказательства.

Теорема 1. (Достаточный признак равномерной сходимости)

Если функция непрерывна по переменной для и существует такая функция , что для и интеграл сходится, то несобственный интеграл сходится равномерно относительно , где .